OI 笑传 #2
神人标题
之前那个算 #1 了
赛时
草草草给这么多部分分全是 subtask 已经感觉不对了。
牛魔的 T1 又是 sb 结论题,还好不知道结论也有 80pts,算你良心。
写完了。我大样例呢?
考一半过来说还有子任务依赖,你大可以不说这个让我安详的趋势。
T2 感觉很 sb 但是又有点不会。
哦我会一个贪心,考虑什么时候会有本来可以正好放下两个棒子但是因为前面放了后面放不了了,此时意味着着两个棒子放置的方案必须都经过前面放的这个棒子,于是只把这个棒子挪挪位置横过来或者竖过来判一下就对了。
判断够不够长直接二维前缀和。
感觉很对啊,写一下。
大样例过了。优势在我。
cnm 又想起来还有子任务依赖,大样例还这么小有个单的优势。
怎么发 T1 大样例了。
我草怎么没过,写个 dfs 怎么你了。
草草草草草草草草为什么不对。
幸好调过了,但是还有 2.25 h。
T3 怎么看不懂。
我草 T4 挺像是之前做过不少的神秘优化建图啊,不写 T3 了看 T4 能不能翻盘。
不是你个唐上次切 T2 不也似在 T1 上被二次翻盘还想着用 T4 翻??
拆点好像就做完了?写一下。
nm 怎么这么难写。
不对啊是假的。我草怎么还有 1h。
欸但是我的是 55pts 做法,优势在我。
怎么调不对。
我草怎么就剩 30min 了。严肃写暴力。
T3 怎么还有 10pts,我写写写写写。
写完吃饭了。
回来一看我草哥们挂成啥了。
T2
主要是说一下处理不相交的思路。
我的结论不知道真假,反正挂成了 0pts。
首先二维前缀和处理每个点可以向左向右向上向下到的最长距离是好想的。
接下来考虑一个段会怎么样影响第二个段的放置。
把题解的图贺过来吧。
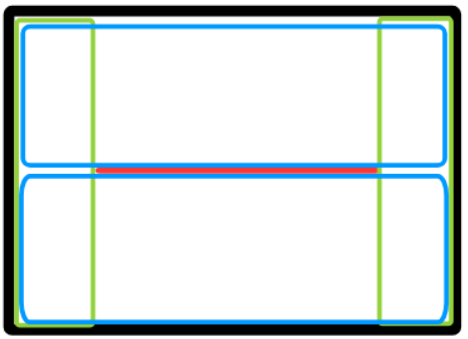
一条线会把整个区间分成四个贴着边的矩形。
于是我们处理一个很重要的东西就是计算出前 \(i\) 行,后 \(i\) 行,前 \(j\) 列,后 \(j\) 列,这四个子矩形内部选取一个长条的最大长度。
这东西还是个用每个点可以向左向右向上向下到的最长距离处理下也是好做的。
那不做完了。
T3
这么深刻的倍增。
考虑从 \(u\) 到 \(v\) 构造数列的过程,就是一个人 \(x\) 的后面可以接 \(y\) 当且仅当存在一个序列使得 \(y\) 出现在 \(x\) 后面,问最少要接多少个人。
有一个很显然的贪心就是如果我们还不可以一步就跳到我们目标的那个人,那我们肯定要往一个序列的尽可能前面跳转。因为这样在这个位置后面的数会才会最多,才会有更大的机会让后面的数包含 \(v\) 从而跳到 \(v\) 以达成目标。
这个性质决定了对于一个特定的位置,跳转到别的序列的位置是唯一确定的。
于是我们可以尝试加速这一过程,用倍增。
这个倍增除了要记录出发的数和跳的步数的 \(k\) 次方外,还要记录跳这么多步数后到的是哪个序列,来方便我们求解答案。
于是设倍增数组 \(fa_{i,k,j}\) 表示从数 \(i\) 按照上述贪心方式跳了 \(2^k\) 步后到了第 \(j\) 个序列的最前面的下标是多少。我们把这个当成 dp 题来做。从小到大枚举 \(k\),首先有初始化:
接下来对于所有的 \(k=0\) ,我们枚举起始的序列 \(p1\) 和一步后到达的序列 \(p2\),同时在到达的序列中倒叙枚举开始的数 \(i\),这样 \(i\) 出现位置的后缀最小值就是当前状态 \(fa_{i,0,p2}\) 的答案。
接下来是 \(\forall k>0\) 的转移。任意顺序枚举数 \(i\),枚举起始的序列 \(p1\) 和一步后到达的序列 \(p2\)。首先可以继承上一轮的状态,也就是 \(fa_{i,k,j}=fa_{i,k-1,j}\)。
接下来就是倍增的套路用 \(k-1\) 轮的状态转移,要取下最小值,这是我们贪心的基本目标。
你会发现 \(k\) 越大,到达的位置一定是越小的。
下面是求解答案的过程,当然要从大到小枚举 \(j\),我们记录一个数组 \(best_i\) 表示调了这么多次之后,能到序列 \(i\) 中的最前面的位置是哪里。
\(best_i\) 的初始值就是各序列中 \(u\) 的位置,这个是显然的。
判断一个 \(best_i\) 状态可以直接取到答案就是在这一列中 \(best_i\) 小于 \(v\) 出现的位置。
这里初始值要特判下是否可以直接存在状态合法,如果存在直接输出 \(1\)。
否则,此时答案至少是 \(2\),这是个小细节。
接下来从各 \(best_i\) 出发,尝试用 \(fa\) 数组跳到更小的值。
如果一轮后无法到达 \(v\),就把 \(2^k\) 步加到答案里面去。
循环结束后,如果答案比序列都长,当然是无解的。
否则就是答案了,直接输出即可。
代码实现一堆细节,但是终于在这一天内结束前三题了。
T4 是个神秘点分树+神秘 dp,不会写。
code
T3
#define psb push_back
#define mkp make_pair
#define ls p<<1
#define rs (p<<1)+1
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e5+5;
const int lgr=24;
int fa[N][30][10];
int rel[9][N];
int arr[9][N];
int main(){
int n,m;cin>>n>>m;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
int x;cin>>x;
arr[i][j]=x;
rel[i][x]=j;
}
}
for(int i=0;i<=n+5;i++){
for(int j=0;j<=m+5;j++)fa[i][0][j]=0x3f3f3f3f;
}
for(int p1=1;p1<=m;p1++){
for(int p2=1;p2<=m;p2++){
int minn=n+1;
for(int i=n;i>0;i--){
minn=min(minn,rel[p2][arr[p1][i]]);
fa[arr[p1][i]][0][p2]=min(fa[arr[p1][i]][0][p2],minn);
}
}
}
for(int k=1;k<=lgr;k++){
for(int i=1;i<=n;i++){
for(int p1=1;p1<=m;p1++){
fa[i][k][p1]=fa[i][k-1][p1];
for(int p2=1;p2<=m;p2++){
fa[i][k][p1]=min(fa[i][k][p1],fa[arr[p2][fa[i][k-1][p2]]][k-1][p1]);
}
}
}
}
int q;cin>>q;
for(int i=1;i<=q;i++){
int u,v;cin>>u>>v;
int best[10],ccb[10];
bool tg=0;
for(int i=1;i<=m;i++){
best[i]=rel[i][u];
if(best[i]<rel[i][v]){
tg=1;break;
}
}
ll res=2;
if(tg){cout<<1<<'\n';continue;}
for(int k=lgr;k>=0;k--){
for(int j=1;j<=m;j++){
ccb[j]=best[j];
for(int ki=1;ki<=m;ki++){
ccb[j]=min(ccb[j],fa[arr[ki][best[ki]]][k][j]);
}
}
tg=0;
for(int l=1;l<=m;l++){
if(ccb[l]<rel[l][v]){
tg=1;break;
}
}
if(!tg){
for(int l=1;l<=m;l++)best[l]=ccb[l];
res+=(1<<k);
}
}
if(res>n)cout<<-1<<'\n';
else cout<<res<<'\n';
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号