树状数组
才发现没从洛谷搬过来(
1. 概述
树状数组究竟是什么?就是省掉一半空间后的线段树加上中序遍历
\(\hspace{8.5cm}\)- NOI2019 Au. zkw
树状数组(Binary Indexed Tree,BIT)是一种树形数据结构,一句话概括它的最基本的作用既是:单点修改,前缀求和。
2. 原理及代码分析
给定一个数组 \(a[1\cdots n]\),对于每次操作,更改某一位置的值或求某一区间的和。
思考一下,我们要实现两种操作:单点修改和区间求和。
对于普通数组而言,单点修改的时间复杂度是 \(O(1)\),但区间求和的时间复杂度是 \(O(n)\)。
当然,我们也可以用前缀和的方法维护这个数组,这样的话区间求和的时间复杂度就降到了
\(O(1)\),但是单点修改会影响后面所有的元素,时间复杂度是 \(O(n)\)。
现在我们希望找到这样一种折中的方法:无论单点修改还是区间查询,它都能不那么慢地完成。
树状数组就是这样的一种数据结构,它巧妙的利用了二进制。
首先考虑求解区间 \([1,7]\) 中数的和,我们先把 \(7\) 转换为二进制,即 \((0111)_2\)。
这样,我们就可以只求出 \(((0110)_2,(0111)_2]\),\(((0100)_2,(0110)_2]\),\(((0000)_2,(0100)_2]\) 的值再合并即可(注意这里的开闭区间),如下图:

那么,为什么我们只求解 \(0,4,6\) 这几个特殊数 组成的区间呢?
观察其二进制的变化规律我们发现:
\((0111)_2\rightarrow (0110)_2\rightarrow (0100)_2\rightarrow (0000)_2\)
其实就是不断地去掉二进制数最右边的一个 \(1\) 的过程。
于是,这个数据结构的组成即使用方法已经呼之欲出了:
我们定义,对于一个数 \(x\),其二进制最右边的一个 \(1\),连带着它之后的 \(0\) 组成的数为函数 \(\operatorname{lowbit}(x)\)。
定义一个数组 \(C_i\),其维护的是原数组 \(A_i\) 中区间 \((i-\operatorname{lowbit}(i),i]\) 的值,如同上文。
那么,将数组 \(C_i\) 维护的原数组 \(A_i\) 中的区间用图表示出来,长这样:
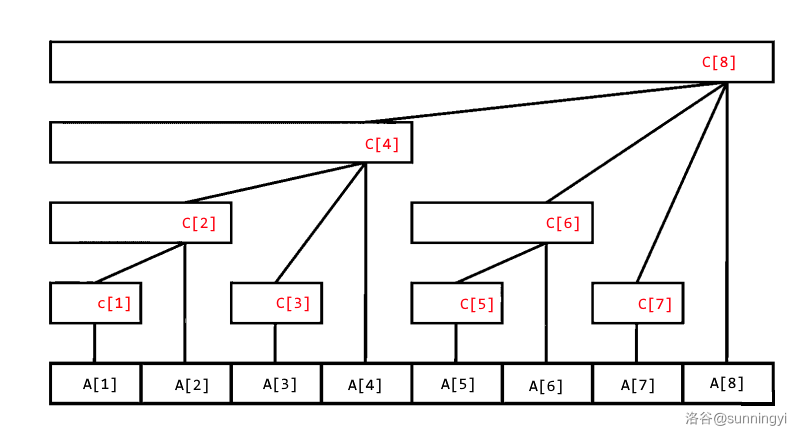
长得很像一棵树(好像就是),所以叫树状数组。
在这里,\(C_i\) 中的值其实和 \(A_i\) 中的并无多大关系:即在进行操作时仅需要用到 \(C_i\) 的值而不再需要 \(A_i\) 的值。
2.1 建树
如上图,其实就是对一个所有节点的值均为 \(0\) 的树状数组作单点修改的过程。
结合下两节的内容可以写出如下代码,这里不多赘述:
for(int i=1;i<=n;i++){
cin>>a[i];
add(i,a[i]);
}
2.2 求 lowbit
有这样一个公式 \(\operatorname{lowbit}(x) = x\ \operatorname{and} \ (-x)\)
由计算机中原反补码的性质可以得到,这里贴一张图:

于是很简单有如下代码:
ll lb(ll x){return x&(-x);}
//lb(x) 即 lowbit(x)。下文的代码中均如此。
2.3 单点修改
因为我们在树状数组中存储的是每一个区间的值,因此在修改过程中需要更新所有包含这个节点的区间节点的值。
那么要更新哪些节点呢?我们举个例子,要更新节点 \(3\) 的值。
则我们用眼可以看出要更新 \(C_3,C_4,C_8\),如下图:
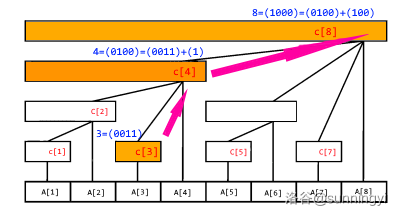
这些更新的下标有什么规律?我们把它们变成二进制:
$(0011)_2 \rightarrow (0100)_2 \rightarrow (1000)_2 $
则我们找到了这样的规律:
对于一个下标为 \(x\) 的节点,其下一个要更改的节点下标为 \(x+\operatorname{lowbit}(x)\)。
于是我们实现一个函数 void add(int p,int k) 表示对下标为 \(p\) 的节点增加 \(k\)。可以很自然的写出如下程序:
void add(int p,int k){
a[p]+=k;
while(p<=n){//当更改的数的下标比数组长度小时才可以继续更改。
c[p]+=k;
p=p+lb(p);
}
}
极致压行版(考场推荐):
void add(int p,int k){
for(;p<=n;p+=lb(p))c[p]+=k;
}
2.4 前缀查询
如我们在开头讨论的求解区间 \([1,7]\) 的过程,如下图:
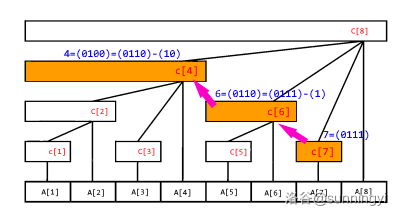
其中访问的下标有这样的规律:
\((0111)_2\rightarrow (0110)_2\rightarrow (0100)_2\)
于是有这样的结论:
对于一个下标为 \(x\) 的节点,其下一个要求和的节点下标为 \(x-\operatorname{lowbit}(x)\)。
我们实现一个函数 ll prefix(int r) 表示求区间 \([1,r]\) 的值的和。可以很自然的写出如下程序:
ll prefix(int r){
ll ans=0;
while(r>0){
ans+=c[r];
r=r-lb(r);
}
return ans;
}
极致压行版(考场推荐):
ll prefix(int r){
ll sum=0;
for(;r>0;r-=lb(r))sum+=c[r];
return sum;
}
2.5 区间查询
即求解出任意 \([l,r]\) 中的所有值的和。
根据我们的经验,可以用前缀和来快速解决,即:
而 \(\operatorname{prefix}\) 函数我们已在上文实现过,因此有函数 ll q(int l,int r) 表示求解 \(\sum_{i=l}^{r} a_i\),程序如下:
ll q(int l,int r){
return prefix(r)-prefix(l-1);
}
完整代码如下:
/*
Template Data Struct
-=Binary Indexed Tree(BIT)=-
*/
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=5e5+5;
int a[N];
int c[N];
int n,m;
//lowbit
ll lb(ll x){return x&(-x);}
//point oper
void add(int p,int k){
a[p]+=k;
while(p<=n){
c[p]+=k;
p=p+lb(p);
}
}
//prefix sum
ll prefix(int r){
ll ans=0;
while(r>0){
ans+=c[r];
r=r-lb(r);
}
return ans;
}
//list sum
ll q(int l,int r){
return prefix(r)-prefix(l-1);
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
a[i]=rd;
add(i,a[i]);
}
for(int i=1;i<=m;++i){
int op;
op=read();
if(op==1){
int p,k;
p=rd;
k=rd;
add(p,k);
}
else{
int l,r;
l=rd;
r=rd;
cout<<q(l,r)<<'\n';
}
}
return 0;
}
3. 实现区间修改,区间求和
少有的我能自己推出来的东西
注意到区间修改,单点求和是其特殊形式,所以我们直接实现区间修改,区间求和即可。
注意到区间修改这一关键词,惊人的做题经验告诉我们有差分数组这个东西。
差分数组有什么性质呢?对于一个数组 \(A_i\),定义其差分数组为 \(d_i\),则有:
当对区间 \([l,r]\) 加 \(k\) 时(\(k\) 可以为负数),只需要将 \(d_l+k\) 和 \(d_{r+1}-k\)。
当查询 \(A_r\) 的值时,其值为:
我们发现这满足树状数组的“前缀求和”的性质。
于是,我们可以用树状数组维护原数组的差分数组,这样即可完成区间修改这一操作,且可以动态求出任意 \(A_i\) 的值。
那么,当我们要求区间 \([l,r]\) 的和时,我们也可以用前缀和的思想,即先求出 \(\sum_{i=1}^{l-1}A_i\) 和 \(\sum_{i=1}^{r}A_i\),之后区间的值就是:
怎样化简这个式子呢?我们先来单独看看这个 \(\sum_{i=1}^{r}A_i\)。
由我们前面的讨论,可以得到:
我们能把这个 \(\sum_{j=1}^{i}\) 拿掉吗?可以!通过画图我们发现,每个 \(d_i\) 被计算的次数是 \(r-i+1\) ,于是原式就变成了:
接下来是一顿化简:
\(\sum_{i=1}^{r}d_i\)?又变成了我们熟悉的样子!
我们发现,\(\sum_{i=1}^{r}i\times d_i\) 中由于 \(i\) 是一个变量,因此我们无法仅通过 \(\sum_{i=1}^{r}d_i\) 推出 \(\sum_{i=1}^{r}i\times d_i\)。
但是,我们大不了就再维护一个 \(i\times d_i\),依然可以用树状数组解决。
于是,原来的式子就变成了:
好像有点吓人?没事,一点一点实现即可。
代码如下:
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=5e5+5;
ll a[N];
ll c1[N];//di 树状数组
ll c2[N];//i*di 树状数组
ll lb(ll x){return x&(-x);}
int n,m;
//适配di树状数组的函数
void add1(int p,ll k){
while(p<=n){
c1[p]+=k;
p=p+lb(p);
}
}
ll prefix1(int r){
ll ans=0;
while(r>0){
ans+=c1[r];
r=r-lb(r);
}
return ans;
}
//适配i*di树状数组的函数
void add2(int p,ll k){
while(p<=n){
c2[p]+=k;
p=p+lb(p);
}
}
ll prefix2(int r){
ll ans=0;
while(r>0){
ans+=c2[r];
r=r-lb(r);
}
return ans;
}
//--------------------------------------
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
a[i]=rd;
}
for(int i=1;i<=n;i++){
add1(i,a[i]-a[i-1]);
}//初始化di树状数组
for(int i=1;i<=n;i++){
add2(i,(a[i]-a[i-1])*i);
}//初始化i*di树状数组
for(int i=1;i<=m;++i){
int op=rd;
if(op==1){
int l,r,k;
l=rd;
r=rd;
k=rd;
add1(l,k);
add1(r+1,-k);
add2(l,l*k);//注意i*di数组的修改(简单的乘法分配律即可推出)
add2(r+1,(r+1)*(-k));
}
else{
int x=rd;
cout<<(x+1)*prefix1(x)-prefix2(x)-(x*(prefix1(x-1))-prefix2(x-1))<<'\n';//那一坨公式
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号