【好题选讲】图论阴间题选讲 II（同余最短路，线段树优化建图及其它杂题）

同余最短路

同余最短路是一种特化的解决整数线性组合问题的算法，尽管线性组合问题可以通过完全背包解决，但当题目的数据较大时，完全背包的时间和空间均会超出限制。

下面用一些题说说同余最短路。

P3403 跳楼机

题意
给定上界 $H$ 和三个步长 $x,y,z \in \mathbb{Z}^+$。考虑通过以下操作生成的数集：

从 $1$ 开始

每次操作可以加上 $x$, $y$ 或 $z$

或重置为 $1$

求该数集中不超过 $H$ 的元素的个数。

数据范围
$1 \leq H \leq 2^{63}-1$
$1 \leq x,y,z \leq 10^5$

原理

$H$ 太大了，怎么办？

考虑找出 $x,y,z$ 三个数中最小的那一个，这里我们让 $x \le y \le z$。

我们给 $x$ 的 $x$ 个同余系 $0\sim x-1$（人话：$\mod x=0,=1\cdots$ 之类这些数的集合）建出点 $0\sim x-1$。

构建同余系就意味着我们要从 $0$ 开始了，于是要先把 $H$ 减一。

之后枚举 $y,z$，枚举同余系点 $i$，向 $(i+y) \mod x$ 点连一条边权为 $y$ 的边，从 $(i+y) \mod x$ 向 $(i+2y) \mod x$ 点连一条边权为 $y$ 的边，以此类推。

最后，钦定 $0$ 节点的最短路为 $0$，初始化其它点的最短路为 $+\infty$，从 $0$ 出发，求解到其它 $x-1$ 个点的单源最短路。

上面的这些操作求出的 $i$ 的最短路的本质就是用 $x,y,z$ 三个数可以组合出的数中，$\mod x=i$ 的最小的数，设这个数为 $k$，然后你会发现 $k+x,k+2x$ 都是可以由 $x,y,z$ 线性组合出来的。那么对于每一个 $k$ 我们计算 $k\sim H$ 中 $k$ 能加多少个 $x$，即下面的式子：

\[\sum_{i=0}^{x-1} \left(\frac{H-k_i}{x} + 1\right) \]

也就是答案了。

你可能会有疑问：你所得到的$\mod x=i$ 的最小的数 $k_i$，是由固定个 $y,z$ 组合出来的，而下面求解答案时并没有再加入 $y,z$。也就是说，所有答案都是在这些 $k_i$ 上加 $x$ 得到的，这真的对吗？

可以这么想：首先不论答案的数是多少，一定都会被分到这几个同余系中。

然后我们既然得到了 $k_i$，之后每次加 $x$，也就是我们答案的同余系是连续的。由于我们证明了这样构造答案的正确性，而且正确答案无法做到在同余系中比连续还要密集，于是这样构造出来的一定就是答案。

~~好阴间的证法~~

优化

求解 $k_i$ 时，我们建出的边的数量是 $O(x)$ 的，若使用 Dijkstra 求解最短的时间复杂度对应是 $O(x\log x)$ 的。但是如果题目给了不是三个数而是 $n$ 个数。对应的时间复杂度就变成 $O(nx \log nx)$，多了的这个 $\log$ 某些时候会被卡。

当然如果边权有负那只能用 SPFA 了，如果边权只有 $01$ 也可以用 01BFS，下面介绍一种方法来让一般的非负权图也有 $O(nx)$ 的求解 $k_i$ 的复杂度。

首先我们尝试在建边时就更新最短路，从 $i$ 向 $(i+y) \mod x$ $y$ 的边，从 $(i+y) \mod x$ 向 $(i+2y) \mod x$，然后你会发现会组成一个环（如果你不理解先别急，下面有例子）。

可以证明环的个数为 $\gcd(x,y)$ 个，各环之间不相交。各环的起始点为 $0\sim \gcd(x,y)-1$。

于是我们直接在环上转着圈一样更新最短路，无需建边。这样做的时间复杂度就是 $O(nx)$ 的。

但是还有个问题：更新最短路时只用转一圈就可以吗？当然是不对的，考虑一个反例，顺便用这个反例讲讲怎么更新：$x=14,y=21,z=30$。

第一次更新时，$\gcd(14,21)=7$，要从 $0 \sim 6$ 开始更新 $7$ 次。但是 $1\sim 6$ 的更新都是在对两端均为 $+\infty$ 的点更新，这里不细说。只有对 $0$ 的更新：$(0+21) \mod 14=7$，更新了 $7$ 的最短路为 $21$。

第二次更新时，$\gcd(14,30)=2$，要从 $0 \sim 1$ 开始更新 $2$ 次。从 $0$ 开始的更新就是给 $2,4,6,8,10,12$ 更新，这里也不细说。但是从 $1$ 开始的更新，更新 $1,3,5$ 时都为 $+\infty$，到达 $7$ 时有了第一次更新的最短路 $21$，于是 $9,11,13$ 的值也可以被更新。然后你会发现可以从 $13$ 到 $1$，于是 $1,3,5$ 的值也可以被更新了。所以如果只转一圈来更新是绝对错误的。

以上的做法被称为两次转圈法求解同余最短路，操作和余数有关似乎复杂实则只需要一个 for 循环就可以实现。一般写两次转圈法。

下面看看这题的代码吧！

Dijkstra 版

Show me the code

#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
ll read(){
  ll x=0,f=1;
  char c=getchar();
  while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
  while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
  return x*f;
}
const int N=1e5+54;
struct e{
  ull v,w;
  bool operator<(const e &x)const{
    return x.w<w;
  }
};
vector<e> edge[N];
ull modi;
ull c(ull a1,ull a2){return (a1+a2)%modi;}
ull dist[N];bool vis[N];
int main(){
  
  ull n,x,y,z;
  cin>>n>>x>>y>>z;
  modi=x;n--;
  for(int i=0;i<x;i++){
    edge[i].push_back(e{c(i,y),y});
    edge[i].push_back(e{c(i,z),z});
  }
  for(int i=0;i<=1e5+5;i++)dist[i]=ULLONG_MAX;
  priority_queue<e> q;
  q.push(e{0,0});
  dist[0]=0;
  while(q.size()){
    ull u=q.top().v;
    ull w=q.top().w;
    q.pop();
    if(vis[u])continue;
    vis[u]=1;
    dist[u]=w;
    for(int i=0;i<edge[u].size();i++){
      ull v=edge[u][i].v;
      ull w=edge[u][i].w;
      if(dist[v]>dist[u]+w){
        dist[v]=dist[u]+w;
        q.push(e{v,dist[v]});    
      }
    }
  }
  ull ans=0;
  for(int i=0;i<x;i++){
    if(dist[i]==ULLONG_MAX||dist[i]>n)continue;
    ans+=((n-dist[i])/x +1);
  } 
  cout<<ans;
  
  return 0;
}

两次转圈法：

Show me the code

#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
ll read(){
  ll x=0,f=1;
  char c=getchar();
  while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
  while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
  return x*f;
}
const int N=1e5+54;
struct e{
  ull v,w;
  bool operator<(const e &x)const{
    return x.w<w;
  }
};
ull dist[N];bool vis[N];
int main(){
  
  ull n,x,y,z;
  cin>>n>>x>>y>>z;
  n--;
  for(int i=0;i<1e5+5;i++)dist[i]=ULLONG_MAX;
  dist[0]=0;
  ull gy=__gcd(x,y);
  for(int i=0;i<gy;i++){
    for(int cur=i,nxt,cyc=0;cyc<2;cyc+=(cur==i?1:0)){
      nxt=(cur+y)%x;
      if(dist[cur]!=ULLONG_MAX)dist[nxt]=min(dist[nxt],dist[cur]+y);
      cur=nxt;
    }
  }
  ull gz=__gcd(x,z);
  for(int i=0;i<gz;i++){
    for(int cur=i,nxt,cyc=0;cyc<2;cyc+=(cur==i?1:0)){
      nxt=(cur+z)%x;
      if(dist[cur]!=ULLONG_MAX)dist[nxt]=min(dist[nxt],dist[cur]+z);
      cur=nxt;
    }
  }
  ull ans=0;
  for(int i=0;i<x;i++){
    if(dist[i]==ULLONG_MAX||dist[i]>n)continue;
    ans+=((n-dist[i])/x +1);
  } 
  cout<<ans;
  
  return 0;
}

本题中，后者比前者快了大约 $50$ms。

ABC077D Small Multiple

题意
求 $K$ 的正整数倍中，数位和的最小值。

数据范围
$2 \leq K \leq 10^5$

神秘一句话题。

首先关于数位和的变化有一个很好玩的性质是：若 $+1$ 不导致进位，则 $+1$ 会导致原数的各数位和 $+1$；无论如何，$\times 10$ 不改变各数位和。

然后我们还是分开 $K$ 的各个同余系然后建好点，对于同余系 $i$，我们向 $i+1$ 连边权为 $1$ 的边，对 $10i \mod K$ 连边权为 $0$ 的边，对应表示变到同余系对应的数所需的数位和变化。

这样，从 $0$ 出发，再回到 $0$ 的最短路就是对应数位和的最小值。

且慢，你不是说在 $+1$ 不导致进位的前提下才有该操作会导致原数的各数位和 $+1$ 这个结论吗，如果从 $i$ 到 $i+1$ 会导致 $K$ 的进位，这个边权还能这样给吗？

实际上，这条边是没有用的。这个不是很会证啊想了一晚上也没想出来，好多题解也没有严谨的证明过这个。有缘再会吧。

code

Show me the code

P2662 牛场围栏

题意
给定 $N$ 种木料及其原始长度 $l_i$，每种木料最多可削短 $M$ 米（必须为整数米）。求无法通过这些木料的长度组合（可重复使用）表示的最大长度。若无解输出 $-1$。

数据范围
$1 < N < 100$
$0 < M < 3000$
$1 < l_i < 3000$

本题是同余最短路求最大不能得到的数例题。

首先给了原始木料长度和能消去的长度相当于给了所有你能得到的木棍长度。然后是一般的同余最短路板子，找出其中木料长度的最小值建出同余系，用两次转圈法更新出最短路。

现在你得到各个同余系 $i$ 中最小的可以用这些数凑出的数字 $k_i$ 了，那么你当然可以算出各个同余系中最大的不能用这些数凑出的数字，也就是 $k-i$。

特殊的，若存在 $k_i=+\infty$，意味着此时这个同余系中所有数都不能表示，即不存在最大值。若可以得到的木料长度存在 $1$，意味着任何长度都可以凑出。特殊判断输出即可。

code

Show me the code

P2371 墨墨的等式

题意
给定 $n$ 个正整数 $a_1,...,a_n$ 和区间 $[l,r]$，求有多少个 $b\in[l,r]$ 使得方程 $\sum_{i=1}^n a_ix_i = b$ 存在非负整数解 $(x_1,...,x_n)$。

数据范围

$n \leq 12$

$0 \leq a_i \leq 5\times 10^5$

$1 \leq l \leq r \leq 10^{12}$

前缀和一下就做完啦。

code

Show me the code

CF786B Legacy

题意
给定 $n$ 个点，$q$ 条有向边，边有边权，边分三种类型：

点 $v$ 到点 $u$ 的边

点 $v$ 到区间 $[l,r]$ 内所有点的边

区间 $[l,r]$ 内所有点到点 $v$ 的边

求从起点 $s$ 到所有点的最短路。

数据范围

$1 \leq n,q \leq 10^5$

$1 \leq s \leq n$

$1 \leq w \leq 10^9$

是一个线段树优化建图，本质还是选讲I中提到的中转节点的思想。

首先关于区间连边肯定不能一条一条连，于是我们参考线段树上给每个段分配的大线段，把这些线段建出点，用 $\log n$ 个点就可以拼成对应的区间。

这里由于有多对单连和单对多连，我们给每个点建出对应的入点和出点，两种点分布在两棵不同的线段树上，出点总是用 $0$ 边连向入点，入点线段树上总是由子段向父段连边，出点线段树上就是父段给对应的子段连边，两棵树根节点之间不能有边，这些边权都是 $0$。

然后单对多的连边就是从入点的原点到出点线段树对应的区间代表的点上连边。多对单就是从入点线段树上对应的点给出点原点连边。这样你就可以开始从 $1$ 跑单源最短路了。

az似乎说起来很难说明白，放个别人的图吧。

（翻其他人的博客）

不是怎么都把两个线段树横着摆，这样有点太乱了，我觉得对顶着更好看，自己画个图吧：

前方多图警告

这是整张图的初始状态

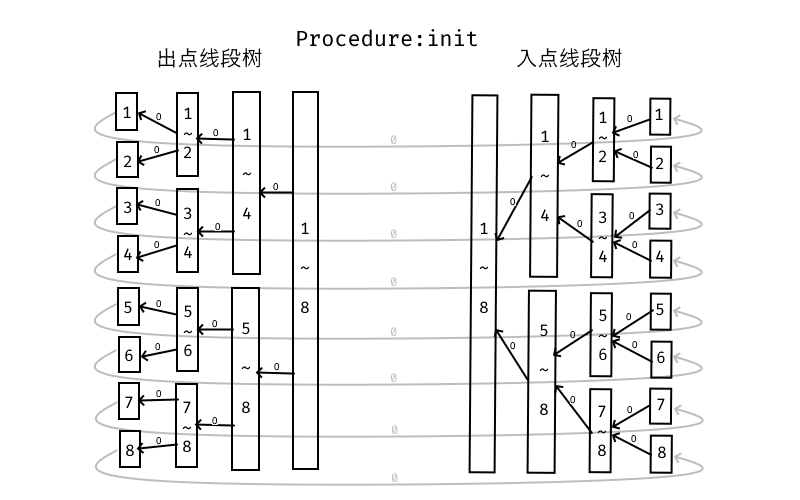
为了方便，下面我们省略连接两点的灰色边。

下面是连接 $2$ 到 $[1,4]$ 的操作例：

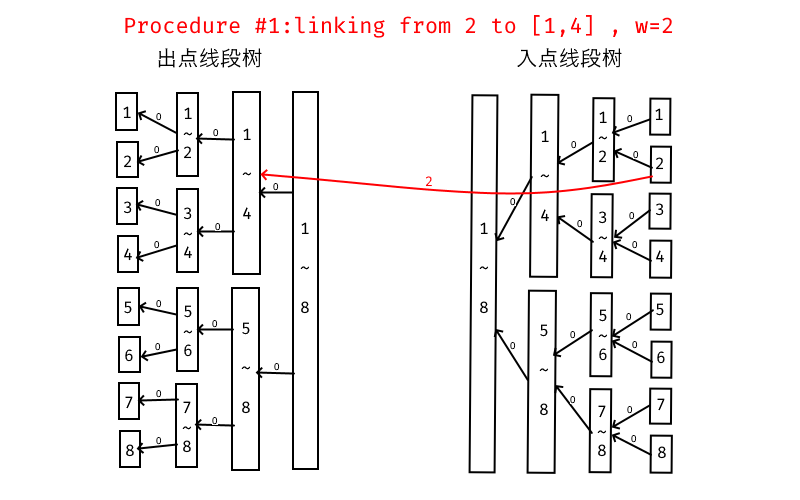
下面是连接 $[3,6]$ 到 $5$ 的操作例：

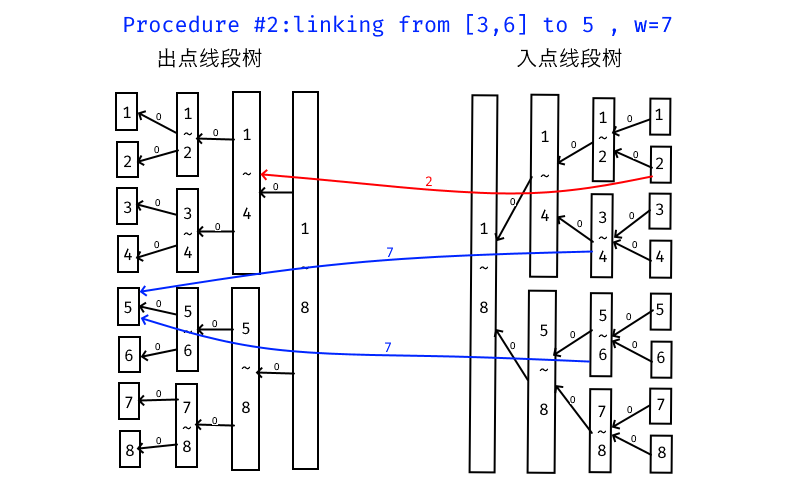
看看代码吧：

code

Show me the code

P7297 [USACO21JAN] Telephone G

题意
给定 $N$ 个点的序列，每个点有类型 $b_i\in[1,K]$。点 $i$ 到 $j$ 的转移代价为 $|i-j|$，且仅当类型 $b_i$ 到 $b_j$ 的转移被允许时才能转移。求从点 $1$ 到点 $N$ 的最小总代价。

数据范围

$1 \leq N \leq 5 \times 10^4$

$1 \leq K \leq 50$

转移矩阵 $S$ 大小为 $K \times K$

首先这个边权的定义很有意思，这意味着如果两点可以直接连接，这条边就是两点之间的最短路。

注意到类型数量很少，我们从类型上入手。

假设我们正在考虑 $k_i$ 类型的点 $u$，向 $k_j$ 类型的点连边，若 $k_j$ 类型的点之间可以互相交流，此时我们仅需在 $k_j$ 类型的点中找到位置最大的不大于自己的点和位置最小的大于自己的点，向着两个点连边即可。

为什么呢？假设 $k_{j1}<k_{j2}<k_{j3}<k_{j4}$，你从 $u$ 向 $k_{j2},k_{j3}$ 连边，若要从 $u$ 到 $k_{j1}$，走 $u \rightarrow k_{j2} \rightarrow k_{j1}$ 与走 $u \rightarrow k_{j1}$ 的边权是相同的。

同理，在相同类型点之间连边时，也只需考虑最大的不大于自己的点和最小的大于自己的点就可以了。

但是，题目中不保证同类之间可以互相连边，这样怎么办？

其实，$u$ 向 $k_j$ 类型的点连边，若 $k_j$ 类型的点不能互相交流，其实与 $k_j$ 类型的点之间可以互相交流是等价的，原因是我们大可以从 $u$ 到 $k_j$ 中的任意一个点，边权是相等的。

但是，如果我们是从 $k_j$ 出发的，此时就不能走同类连的边了，这里特判一下即可。

这样建图的边数是 $O(nK)$ 的，可以通过本题。

code

Show me the code

P4366 [Code+#4] 最短路

题意
给定 $N$ 个点的图，任意两点 $i,j$ 间有双向边，边权为 $(i \oplus j) \times C$。另有 $M$ 条单向边，求从 $A$ 到 $B$ 的最短路。

数据范围

$1 \leq N \leq 10^5$

$0 \leq M \leq 5 \times 10^5$

$1 \leq C \leq 100$

单向边权 $1 \leq V_i \leq 100$

看到位运算先想拆位。

然后本题有个很有用的性质是点权连续，举个例子，如果点权为 $101110_2$，那么点权为 $100000_2,\ 001000_2,\ 000100_2, \ 000010_2$ 的点也是存在的。

此时我们可以把 $i,j$ 之间的异或拆成 $i$ 和 $j$ 的各位之间分别异或，而由上面的性质可以知道有 $j$ 的各位的点权的点一定是存在的。于是我们仅需在每个点建出连向能造成加法的独立各位点权的点就好了。

这么说太抽象了，举个例子，给 $01100_2$ 连边，仅需连向 $01100_2 \oplus 10000_2=11100_2, \ 01100_2 \oplus 01000_2=00100_2,\ 01100_2 \oplus 00100_2=01000_2,\ 01110_2,\ 01101_2$ 点就可以了，边权为 $2^j \times C$。

这样，总边数为 $O(n\log n)$，可以通过。

似乎可以被称作异或的向量性质？

code

Show me the code

ABC164E Two Currencies

题意
给定 $n$ 个城市的双向道路网络，每条道路需要银币 $x_i$ 和时间 $t_i$。每个城市可用金币兑换银币（汇率 $c_i$，耗时 $d_i$）。初始在 $1$ 号城市，有 $s$ 银币和无限金币，求到达各城市的最小时间。

数据范围

$2 \leq n \leq 50$

$n-1 \leq m \leq 100$

$1 \leq x_i \leq 50$

$1 \leq t_i,d_i \leq 10^9$

$1 \leq s,c_i \leq 10^9$

可以发现从 $1$ 到 $n$ 最多需要 $5000$ 个银币，于是我们之直接按照银币数量建出分层图，根据银币的数量变化建边，然后最短路即可。

code

Show me the code

APIO2023 cyberland

题意
给定包含 $N$ 个节点和 $M$ 条边的无向图，边权为通行时间。每个节点有三种类型：

类型0：可将当前总时间清零

类型1：无特殊效果

类型2：可将当前总时间减半（最多使用 $K$ 次）

求从节点0到节点 $H$ 的最短通行时间。

数据范围

$2 \leq N \leq 10^5$

$0 \leq M \leq \min(10^5, \frac{N(N-1)}{2})$

$1 \leq K \leq 10^6$

$1 \leq H < N$

边权 $1 \leq c[i] \leq 10^9$

保证 $arr[0] = arr[H] = 1$

~~伟大的 APIO 竞赛即将开赛了✋😭🤚✋😭🤚✋😭🤚~~

现在应该对除以二这个操作很敏感才对，即使题目有精度要求，我们也可以知道一定不会使用减半能力 $100$ 次以上，因此这个 $K\le 10^6$ 其实在诈骗。

于是我们直接按照使用减半能力次数建出分层图。然后考虑这个清零能力怎么处理。首先不论我们的时间消耗多少，只要我们能够到达有这个能力的点，我们就可以从时间 $0$ 开始，也就是说，所有能从 $0$ 节点到达的有这个能力的点都作为起点参与最短路计算即可。

但是这里有个小坑，就是我们到达 $H$ 后就不能再离开 $H$，因此我们可以先建出不包括 $H$ 的分层图，跑完最短路以后再去更新 $H$ 点就好了。

code

Show me the code

EC Final 2022 - Chase Game

题意
给定无向无权图 $G=(V,E)$，其中 $|V|=n$, $|E|=m$。定义两个玩家：

Shou 初始在顶点 $1$，目标顶点 $n$

Pang 初始在顶点 $k$

每轮移动规则：

Shou 选择移动至相邻顶点 $u\rightarrow v$

计算当前最短距离 $dis = \mathrm{dist}(v,k)$

伤害计算：

\[\text{damage} = \begin{cases} d - dis & \text{if } dis < d \\ d & \text{otherwise (Pang 传送至 $v$)} \end{cases} \]

求 $1\rightarrow n$ 路径的最小总伤害。

数据范围

$n \leq 10^5$, $m \leq 2\times 10^5$

$d \leq 2\times 10^5$

保证图连通

首先想想如果 S 一开始就在 P 攻击范围外和 S 与 P 开始时重合怎么做，显然两种情况等价。

这里引出一个结论：若 S 的移动不导致 P 移动，则到达一点受到的伤害的最小值就是沿着最短路得到的。

因为移动受到的伤害一定是 $d,d-1,d-2$ 这样，你可能会问为什么不会存在 $d,d-1,d-1$ 这样，因为伤害是通过最短路结算的，这意味着受到伤害为 $d$ 的点一定有至少一条边连接了第三个 $d-1$ 的点，我们直接从 $d$ 到第三个 $d-1$ 即可。

又因为我们收到的伤害逐渐减小，也就是离 P 教授越来越远，我们一定是离目标点越来越近的，不可能出现移动一次距离目标点路径不变的情况，证明同上，也就是在走最短路。

这样，属于上面两种情况的只需要找到起点到终点的最短路即可。现在想想在攻击范围内不重合的情况。

我们可以预处理出在不导致 P 瞬移的情况下，到达各点收到伤害的最小值是多少，也就是求出各点从起点出发，距离 P 不超过 $d$ 的点的最短路。

然后，我们再从终点出发，求出终点到各点的最短路，此时枚举距离 P 不超过 $d$ 的点，把两段最短路拼起来取最小就是答案。

code

Show me the code

JOI 2020 Final - Olympic Bus

题意
给定有向图 $G=(V,E)$，每条边 $e_i=(u_i,v_i,c_i,d_i)$。定义操作：

翻转边 $e_i$ 为 $(v_i,u_i)$，产生代价 $d_i$

只能进行该操作一次，设 $\text{dis}(1\rightarrow n)$ 为 $1$ 到 $n$ 的最短路长度，求最小化的 $\text{dis}(1\rightarrow n) + \text{dis}(n\rightarrow 1) + d$。

数据范围

$2 \leq n \leq 200$

$1 \leq m \leq 5\times 10^4$

$0 \leq c_i \leq 10^6$

$0 \leq d_i \leq 10^9$

小科技：最短路树。

还记得最短路的三角形不等式吗？如果边 $(i,j)$ 的边权 $w$ 就是让 $d_i+w=d_j$ 成立的 $w$，我们把 $w$ 放进最短路树中。当然如果全都放进去的话是个 DAG，但是这个题中我们仅需要树就可以了，在这个题中，我们要从每一个入度为 $0$ 的点开始求最短路，这些都是为了保证下文的一些结论正确。

对应 $\text{dis}(1\rightarrow n), \ \text{dis}(n\rightarrow 1)$，我们分别以 $1,n$ 求解单源最短路，建出两棵最短路树，此时树上的边的数量是 $O(n)$ 的，因为是一棵树。

如果在原图的反图上以 $1,n$ 求解单源最短路，我们相当于求解出了各个点到 $1,n$ 的最短距离，这里定义 $i \to 1$ 为 $s_i$，$i\to n$ 为 $t_i$。

接下来，我们枚举所有边 $e(i,j)$。如果这条边在任意一棵最短路树上，反转这个边将会破坏最短路，此时需要重新以 $1,n$ 求解单源最短路。

如果这个边不在最短路树上，那么这条边无论是翻转还是消失都不会影响 $s_i,s_j,t_i,t_j$ 的值，因为若在反图上 $s_j+w=s_i$，对应在正图上也会有 $d_i+w=d_j$ 即此边在最短路树上，矛盾了，$t$ 的情况同理；也不会影响原来最短路的值，这个应该很好理解。然后就是这条边反转以后，经过这条边从 $1\to n$ 的最短路径长一定是 $s_j +w + t_i$，经过这条边从 $n\to 1$ 的最短路径长一定是 $t_j + w+s_i$，把这两个和最短路树上的全局最短路比大小更新答案就好了。

code

Show me the code

USACO15JAN Grass Cownoisseur G

题意

给定有向图 $G=(V,E)$，求从节点 $1$ 出发并返回的路径中，最多逆向一条边的情况下能访问的最大不同节点数。

数据范围

节点数 $|V|=N$：$1 \leq N \leq 10^5$

边数 $|E|=M$：$1 \leq M \leq 10^5$

保证无重边

和上面那题挺像的？但是比上面的题简单。

建分层图，层间连边代表原图中的逆向边。因为最后还要回到节点 $1$，于是我们给 $1$ 单独开个点，从别的点连向 $1$ 的边就连在这个点上，然后给原图缩点，在缩点后图上拓扑排序即可。

code

Show me the code

posted @ 2025-05-05 15:03 hm2ns 阅读(78) 评论(0) 收藏举报

刷新页面返回顶部

hm2nsite

不过总有一天，我的心会游过夜晚，游到走累的你的身边

【好题选讲】图论阴间题选讲 II（同余最短路，线段树优化建图及其它杂题）

更多知识

同余最短路

P3403 跳楼机

原理

优化

ABC077D Small Multiple

P2662 牛场围栏

P2371 墨墨的等式

CF786B Legacy

前方多图警告

P7297 [USACO21JAN] Telephone G

P4366 [Code+#4] 最短路

ABC164E Two Currencies

APIO2023 cyberland

EC Final 2022 - Chase Game

JOI 2020 Final - Olympic Bus

USACO15JAN Grass Cownoisseur G

公告