带权并查集

前言

一般的并查集仅维护了节点和集合的关系，对集合内部各元素间的关系未作处理。此时如果我们还需要有关各个节点之间的信息，就需要给节点加入权值并动态更新它，这样的并查集结构称为带权并查集。

这篇文章通过一些例题讲解带权并查集的原理和应用。

题目 1. 数轴上任意两点之间的距离问题

问题简述：

数轴上面有 \(n\) 个点，只给你 \(m\) 条两个点之间的相对位置信息，之后有 \(q\) 次询问，每次询问任意两点之间的距离，要求你在 \(O(n+m+q)\) 的时间内解决这个问题。

距离信息的描述定义如下：

• A B 100 表示从 \(A\) 开始向右走 \(100\) 个单位长度可以到达 \(B\) 点。
• A B -100 表示从 \(A\) 开始向左走 \(100\) 个单位长度可以到达 \(B\) 点。

注意：如果你无法求解出两点之间距离，请给出一行 idn。

保证数据之间没有矛盾。

不妨先来考虑一下弱化版：不问距离，只问能否求解出距离，如何解决？

从物理学中参考系的角度考虑：如果两个点都与同一个点有联系，自然可以求解出两个点之间的相对距离。我们建立并查集，通过关系维护集合，判断即可。

但是题目要求距离，我们能否把距离这一变量放在并查集的点上呢？

可以！顺着前面的思路，我们令一个点的权值表示为自己到自己的子集头部节点的相对距离，假设用 \(d\) 表示。头节点到子集的距离显然是 \(0\)。

但是如此表示之后，原来并查集的路径压缩和合并操作还能正常用吗？

举例子试试：先是合并操作

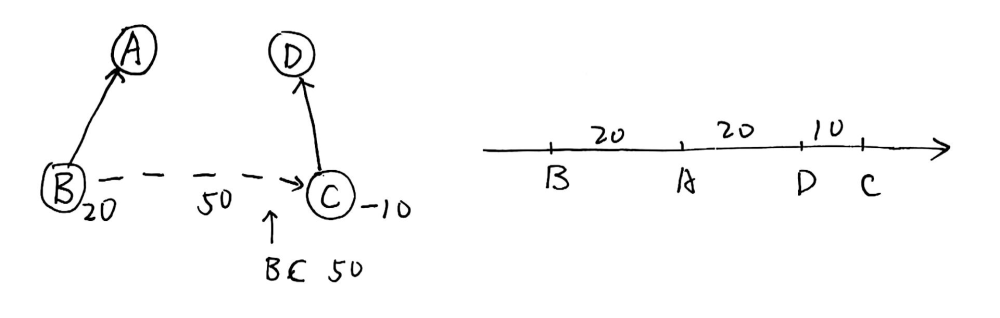
我们希望的是：

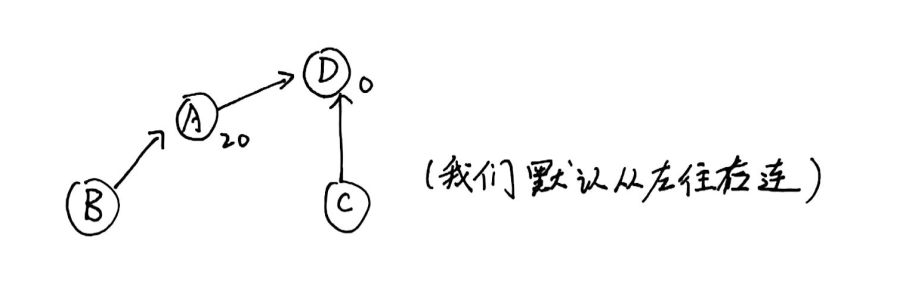
\(B,C\) 原来的值与这两个点之间的相对距离 \(50\) 之间有什么关系呢？

注意到：

\[-10 - 20 +50 =20 \]

即：

\[d_C-d_B+v=d_A \]

是否如此呢？再来一个更一般的例子：

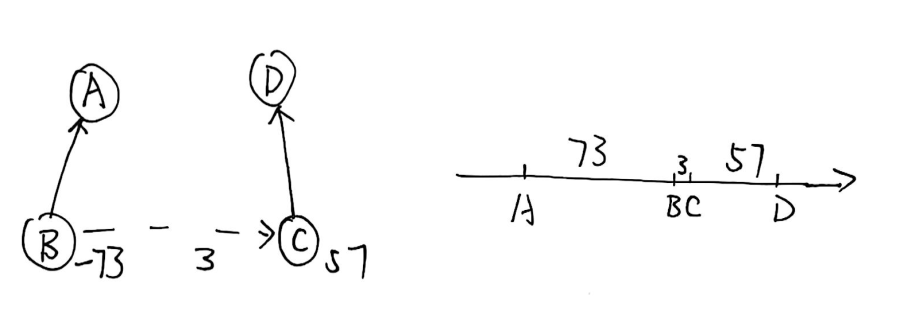
我们希望的：

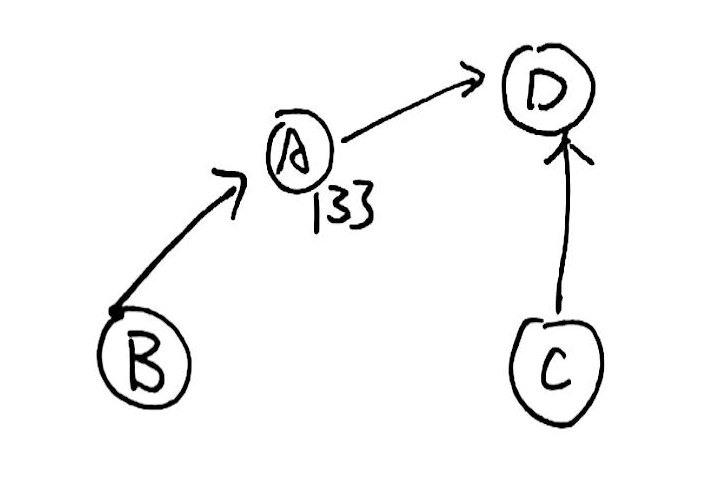
验证？

\[57 - \left ( -73 \right ) +3 = 133 \]

成立！

一般的带权并查集题目，猜个公式之后举几个例子验证之后成立就可以直接用了，无需严谨证明（其实是不会证（（

但是注意到我们的合并操作仅是针对上例中 \(A,D\) 点的数值修改，回到我们对于带权并查集的点权的定义，\(A\) 其下的那些节点们的权值怎么办？

办法是懒更新，在用到这些数据前，我们不管这些值的对错。

如何修正这些值呢？这一过程可以在原并查集结构的路径压缩过程中完成，还是上例：

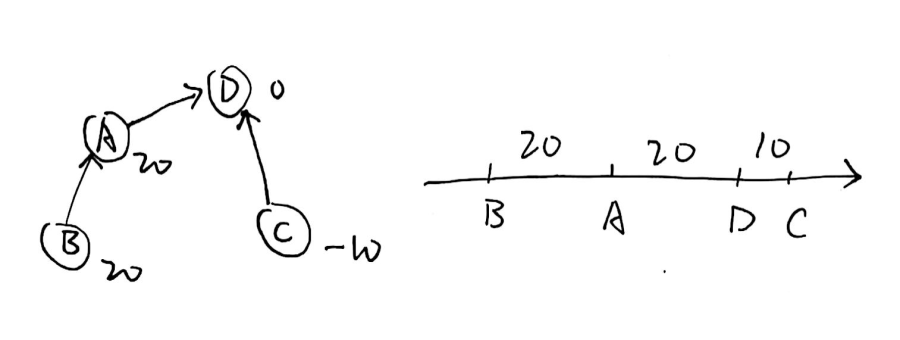
我们希望的：

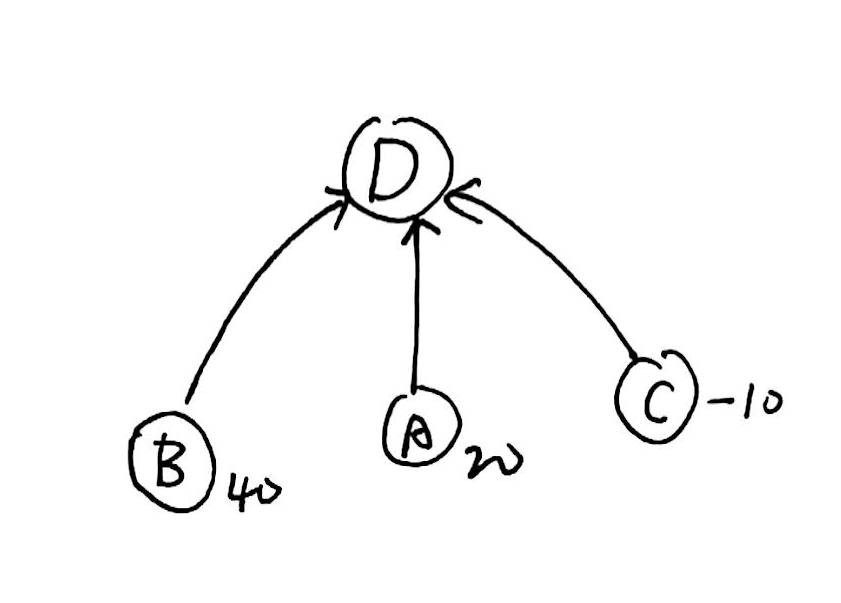
注意虽然 \(B\) 的值是不正确的，但是它相对于 \(A\) 的值一定是正确的，如果我们得到了 \(A\) 的正确值，\(B\) 的正确值当然也可以被更新，显然这是一个递归过程。

在路径压缩时，一旦回到了 \(u\) 点，意味着我们已经得到了 \(u\) 点原来祖先的正确值。由 \(40=20+20\)，我们猜想：

\[d_{B正确} =d_B+d_{A正确} \]

这正确吗？再举一例：

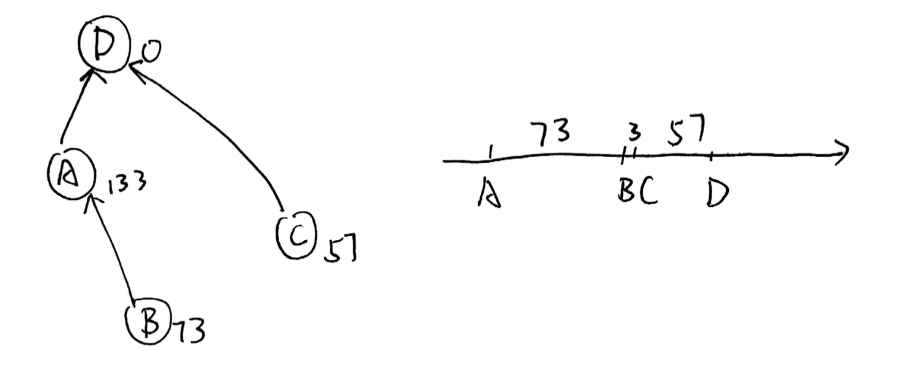
我们希望的：

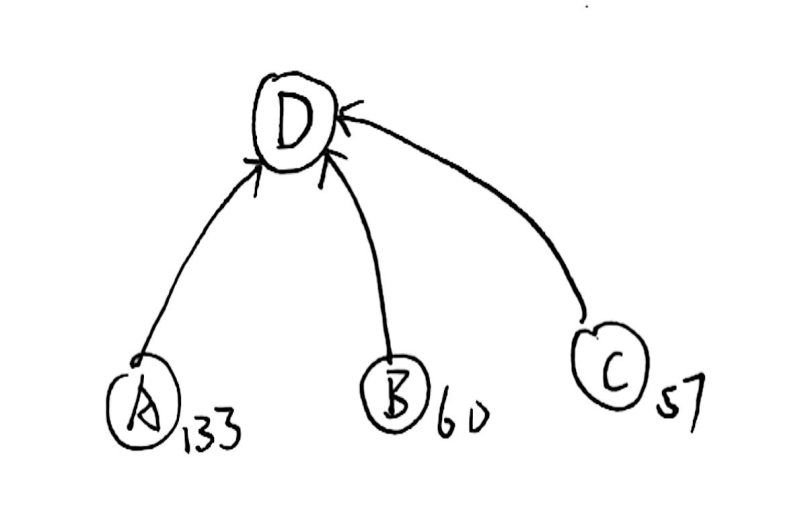
验证？

\[133+\left ( -73 \right) = 60 \]

正确！

既然如此，我们就可以在路径压缩的过程中顺手修正 \(B\) 的值了。

关于答案，因为只要求两点之间距离，因此用两点之间到头节点的相对距离做差即可。但若两点不在同一集合内，应给出 idn 。

这就是并查集最基础的例题了，下面是代码：

const int N=2e5+5;
ll fa[N],dis[N];
int _find (int u){
  if(fa[u]==u)return u;
  int prev=fa[u];
  fa[u]=_find(fa[u]);
  dis[u]+=dis[prev];
  return fa[u];
}
int main(){
  
  int n,m,q;
  cin>>n>>m>>q;
  for(int i=1;i<=n+1;i++){
    fa[i]=i;
    dis[i]=0;
  }
  for(int i=1;i<=m;i++){
    ll l,r,s;
    cin>>l>>r>>s;
    int t1=_find(l),t2=_find(r);
    if(t1!=t2){
      fa[t1]=t2;
      dis[t1]=dis[r]-dis[l]+s;
    }
  }
  for(int i=1;i<=q;i++){
    int l,r;
    cin>>l>>r;
    int t1=_find(l),t2=_find(r);
    if(t1!=t2){
      cout<<"idn"<<'\n';
    }
    else{
      cout<<dis[l]-dis[r]<<'\n';
    }
  }

  return 0;
}

题目 2 蓝桥杯 2022 省 A - 推导部分和

题意简述：

对于一个长度为 \(N\) 的整数数列 \(A_{1}, A_{2}, \cdots A_{N}\)，想知道下标 \(l\) 到 \(r\) 的部分和 \(\sum\limits_{i=l}^{r}A_i=A_{l}+A_{l+1}+\cdots+A_{r}\) 是多少。

仅给定它的 \(M\) 个部分和的值。其中第 \(i\) 个部分和是下标 \(l_{i}\) 到 \(r_{i}\) 的部分和 \(\sum_{j=l_{i}}^{r_{i}}=A_{l_{i}}+A_{l_{i}+1}+\cdots+A_{r_{i}}\), 值是 \(S_{i}\) 。

对于每个询问, 输出一行包含一个整数表示答案。如果答案无法确定, 输出 UNKNOWN。

把区间的和看成两点之间的距离，然后就做完了。

但是在这里要注意一些实现上的细节。由于此题中为一个个数字位置，但是原模型中是一个个抽象的点，于是我们用位置之间的间隔的距离来表示数字位置之间的距离。这也算是一个常用的小 trick 了。

const int N=2e5+5;
ll fa[N],dis[N];
int _find(int u){
  if(fa[u]==u)return u;
  int prev=fa[u];
  fa[u]=_find(fa[u]);
  dis[u]+=dis[prev];
  return fa[u];
}
int main(){
  
  int n,m,q;
  cin>>n>>m>>q;
  for(int i=1;i<=n+1;i++){
    fa[i]=i;
    dis[i]=0;
  }
  for(int i=1;i<=m;i++){
    ll l,r,s;
    cin>>l>>r>>s;
    r++;
    int t1=_find(l),t2=_find(r);
    if(t1!=t2){
      fa[t1]=t2;
      dis[t1]=dis[r]-dis[l]+s;
    }
  }
  for(int i=1;i<=q;i++){
    int l,r;
    cin>>l>>r;
    r++;
    int t1=_find(l),t2=_find(r);
    if(t1!=t2){
      cout<<"UNKNOWN"<<'\n';
    }
    else{
      cout<<dis[l]-dis[r]<<'\n';
    }
  }
    
  return 0;
}

题目 3 [HNOI2005] 狡猾的商人

题意简述：

有一个账本，账本上记录了 \(n\) 个月以来的收入情况，其中第 \(i\) 个月的收入额为 \(a_i\)，\(i=1,2,\ldots,n-1,n\)。当 \(a_i>0\) 时表示这个月盈利 \(a_i\) 元，当 \(a_i<0\) 时表示这个月亏损 \(|a_i|\) 元。所谓一段时间内的总收入，就是这段时间内每个月的收入额的总和。

知道 \(m\) 段时间内的总收入，你的任务是根据记住的这些信息来判断账本是不是假的。

把月份之间的收入当作两点之间的距离，然后就做完了。

判断冲突的方法也很简单，读入数据时如果能够求出两点之间的距离，求一下比较一下就可以了。

代码几乎与 题目 2 没区别。

const int N=2e5+5;
ll fa[N],dis[N];
int _find(int u){
  if(fa[u]==u)return u;
  int prev=fa[u];
  fa[u]=_find(fa[u]);
  dis[u]+=dis[prev];
  return fa[u];
}
int main(){
  
  int T;
  cin>>T;
  while(T--){
    memset(fa,0,sizeof fa);
    memset(dis,0,sizeof dis);
    int n,m;
    cin>>n>>m;
    bool la=0;
    for(int i=1;i<=n+1;i++){
      fa[i]=i;
      dis[i]=0;
    }
    for(int i=1;i<=m;i++){
      if(la==1)break;
      ll l,r,s;
      cin>>l>>r>>s;
      r++;
      int t1=_find(l),t2=_find(r);
      if(t1!=t2){
        fa[t1]=t2;
        dis[t1]=dis[r]-dis[l]+s;
      }
      else{
        ll cd=dis[l]-dis[r];
        if(cd!=s){
          cout<<"false"<<'\n';
          la=1;
        }
      }
    }
    if(la){
      continue;
    }
    else{
      cout<<"true"<<'\n';
    }
  }

  return 0;
}

题目 4 [NOI2002] 银河英雄传说

题意简述：

问题
杨威利会发布合并指令 M i j，将第 i 号战舰所在的队列整体接到第 j 号战舰所在队列的尾部。莱因哈特会发布询问指令 C i j，询问第 i 号战舰和第 j 号战舰是否在同一列，如果在，输出它们之间的战舰数量；否则输出 -1。

输入

• 第一行：整数 T，表示指令总数（\(1 \le T \le 5 \times 10^5\)）。
• 接下来 T 行：每条指令为 M i j 或 C i j，其中 \(1 \le i,j \le 30000\)，且 M i j 保证 i 和 j 不在同一列。

输出

• 对于每条 C i j 指令，输出一个整数，表示 i 和 j 之间的战舰数量；若不在同一列，输出 -1。

注意

• 指令中不存在 i = j 的情况。

---

题意简化 by deepseek

依然是任意两点间的距离模型，但是距离一定是头和尾之间的距离，因此在每个集合里记录一下头和尾就完事了。

贴一个侏罗纪时候写的丑陋代码：

Show me the code

#include<bits/stdc++.h>
using namespace std;
struct lis{
  int fa;
  int son;
  int id;
}ship[30005];
int lcaship[30005],bel[30005];
inline int read(){
  int x=0,f=1;
  char c=getchar();
  while(c<'0'||c>'9'){
    if(c=='-'){
      f=-1;
    }
    c=getchar();
  }
  while(c<='9'&&c>='0'){
    x=(x<<3)+(x<<1)+(c^48);
    c=getchar();
  }
  return x*f;
};
int f_find(int unit){
  if(lcaship[unit]==unit)return unit;
  else {
      int rf=f_find(lcaship[unit]);
      ship[unit].id+=ship[lcaship[unit]].id;//+1;
    lcaship[unit]=rf;
    return lcaship[unit];
  }
}
int s_find(int unit){
  if(ship[unit].son==unit)return unit;
  else return s_find(ship[unit].son);
}
void upd(int unit){
  ship[unit].id=ship[ship[unit].fa].id+1;
  if(ship[unit].son==unit)return;
  else upd(ship[unit].son);
}
int main(){

  int com;
  cin>>com;
  for(int i=1;i<=30003;i++){
    ship[i].fa=i;
    ship[i].son=i;
    ship[i].id=0;
    lcaship[i]=i;
    bel[i]=1;
  }
  for(int i=1;i<=com;i++){
    char op;
    cin>>op;
    int u1,u2;
    u1=read();
    u2=read();
    if(op=='M'){
      int t1=f_find(u1),
        t2=f_find(u2);
      ship[t1].id=ship[t1].id+bel[t2];
      ship[t1].fa=t2;
      lcaship[t1]=t2;
      bel[t2]+=bel[t1];
      bel[t1]=0;
    }
    else{
      int t1=f_find(u1),
        t2=f_find(u2);
      if(t1==t2){
        cout<<max(ship[u1].id,ship[u2].id)-min(ship[u1].id,ship[u2].id)-1<<'\n';
      }
      else{
        cout<< -1<<'\n';
      }
    } 
  } 
  
  return 0;
}

题目 5 除法求值

题意简述：

已知条件

• 给定一个变量对数组 equations 和一个实数值数组 values，其中 equations[i] = [Ai, Bi] 和 values[i] 表示等式 Ai / Bi = values[i]。
• 每个 Ai 或 Bi 是一个表示变量的字符串。

问题

• 给定一个查询数组 queries，其中 queries[j] = [Cj, Dj]，表示询问 Cj / Dj 的值。
• 根据已知条件，计算每个查询的结果。如果无法确定结果，则返回 -1.0。

输出

• 返回一个数组，包含所有查询的结果。

注意

1. 输入总是有效的，不存在除数为 0 或矛盾的结果。
2. 如果查询中的变量未在 equations 中出现，则结果为 -1.0。

---

题意简化 by deepseek

首先把代表变量的字符串用 map 映射成下标，然后把除法关系变成倍数关系。

还记得原模型中的公式吗？

\[d_C-d_B+v=d_A \]

\[d_{B正确} =d_B+d_{A正确} \]

我们也把倍数关系当作距离，只不过这里变成了乘法，于是我们理所当然的猜想公式要变成：

\[d_C \div d_B \times v=d_A \]

\[d_{B正确} =d_B \times d_{A正确} \]

验证一下发现是正确的，于是这题做完了。

Show me the code

class Solution {
public:
    int fa[1100];
    double dis[1100];
    double _find(int u){
      if(fa[u]==u)return u;
      int prev=fa[u];
      fa[u]=_find(fa[u]);
      dis[u]*=dis[prev];
      return fa[u];
    }
    vector<double> calcEquation(vector<vector<string>>& equations, 
                                vector<double>& values, 
                                vector<vector<string>>& queries) {
      map<string,int> mp;
      int at=1;
      for(auto str:equations){
        if(mp.find(str.front())==mp.end()){
          mp[str.front()]=at;
          at++;
        }
        if(mp.find(str.back())==mp.end()){
          mp[str.back()]=at;
          at++;
        }
      }
      int n=mp.size();
      for(int i=0;i<=n+1;i++){
        fa[i]=i;
        dis[i]=1;
      }
      for(int i=0;i<equations.size();i++){
        int u=mp[equations[i].front()];
        int v=mp[equations[i].back()];
        double dist=values[i];
        int t1=_find(u);
        int t2=_find(v);
        if(t1!=t2){
          fa[t1]=t2;
          dis[t1]=dis[v]/dis[u]*dist;
        }
      }
      vector<double> res;
      for(auto str:queries){
        if(mp.find(str.front())==mp.end()||mp.find(str.back())==mp.end()){
          res.push_back(-1.0);
          continue;
        }
        int u=mp[str.front()];
        int v=mp[str.back()];
        int t1=_find(u);
        int t2=_find(v);
        if(t1!=t2){
          res.push_back(-1.0);
        }
        else{
          res.push_back(dis[u]/dis[v]);
        }
      }
      
      return res;
    }
};

题目 6 NOI2001 食物链

题意简述：

背景
动物王国中有三类动物 \(A, B, C\)，食物链构成环形：\(A\) 吃 \(B\)，\(B\) 吃 \(C\)，\(C\) 吃 \(A\)。现有 \(N\) 个动物，编号为 \(1 \sim N\)，每个动物属于 \(A, B, C\) 中的一种，但具体种类未知。

问题
有 \(K\) 句话描述这些动物的关系，每句话格式为：

1. 1 X Y：表示 \(X\) 和 \(Y\) 是同类。
2. 2 X Y：表示 \(X\) 吃 \(Y\)。

每句话可能是真话或假话。假话的判断规则如下：

1. 与前面某些真话冲突。
2. \(X\) 或 \(Y\) 的编号大于 \(N\)。
3. 表示 \(X\) 吃 \(X\)（自己吃自己）。

任务
根据给定的 \(N\) 和 \(K\) 句话，计算假话的总数。

---

题意简化 by deepseek

本题中，我们尝试用带权并查集维护种类关系。

题目中的物种之间有这样的关系：

\[A \underrightarrow{吃}B \underrightarrow{吃}C\underrightarrow{吃}A \]

注意到任意的两个物种之间只可能有两种关系：

• \(x,y\) 同类。
• \(x\) 吃 \(y\)。
• \(x\) 被 \(y\) 吃。

这样的关系在食物链上有那些距离的规律？

• \(x,y\) 同类，则 \(x,y\) 之间的距离为 \(0\)。
• \(x\) 吃 \(y\)，则 \(x,y\) 之间的距离为 \(1\)。
• \(x\) 被 \(y\) 吃，则 \(x,y\) 之间的距离为 \(2\)。

这样的关系能否用我们的相对距离模型表示呢？

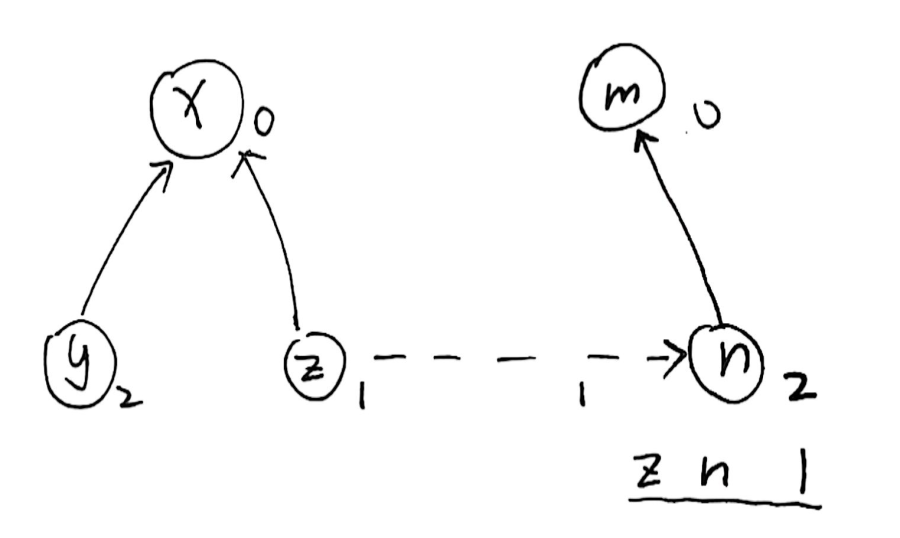
直接看可能不好理清关系，我们不妨带入具体的 \(A,B,C\)：

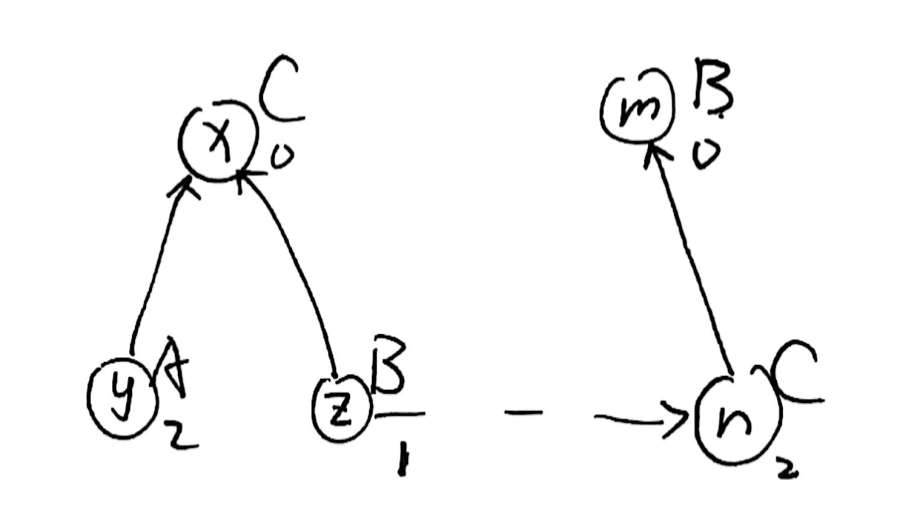
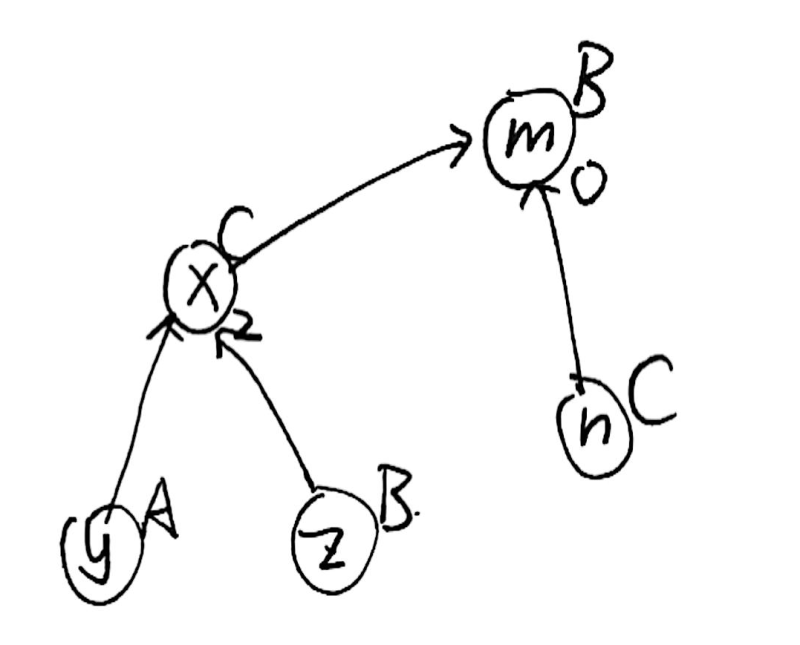
公式还成立吗？\(2-1+1=2\)，成立！

再举一例试试：

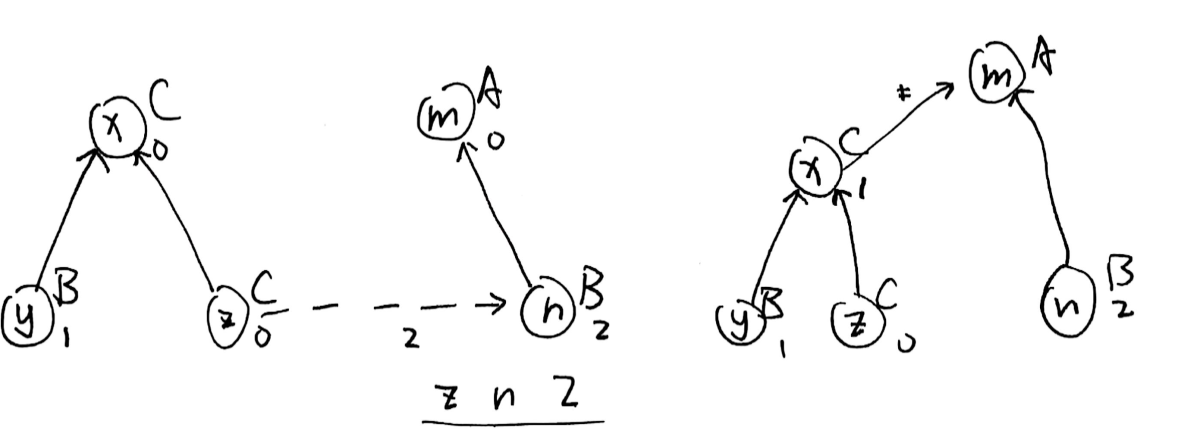
公式还成立吗？\(2-0+2=4\)，\(4\) 是什么？

注意到我们一共有三个关系，且有循环特征，我们自然想到把得到的结果对 \(3\) 取模。可以发现，对 \(3\) 取模后的结果就是正确的答案。

再来看看路径压缩时的情况：

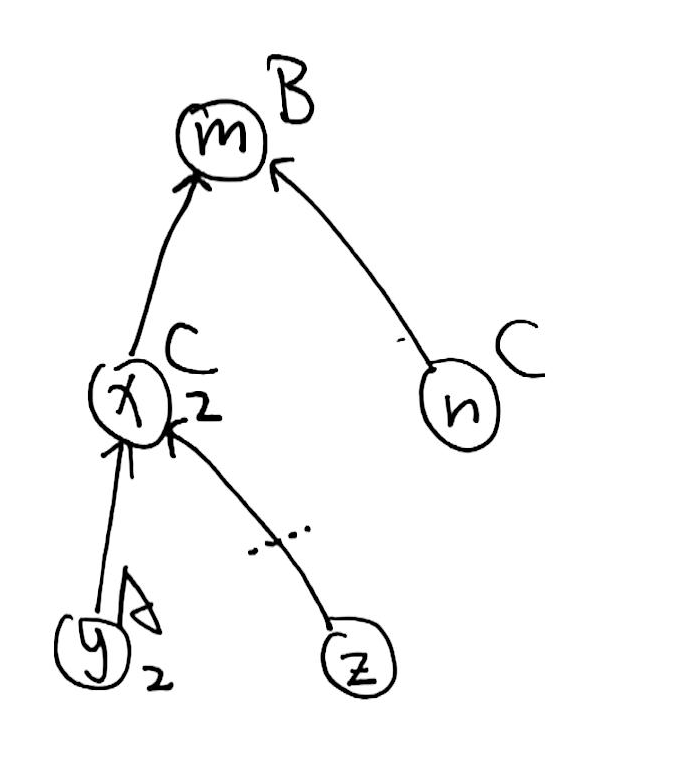
我们想要的：

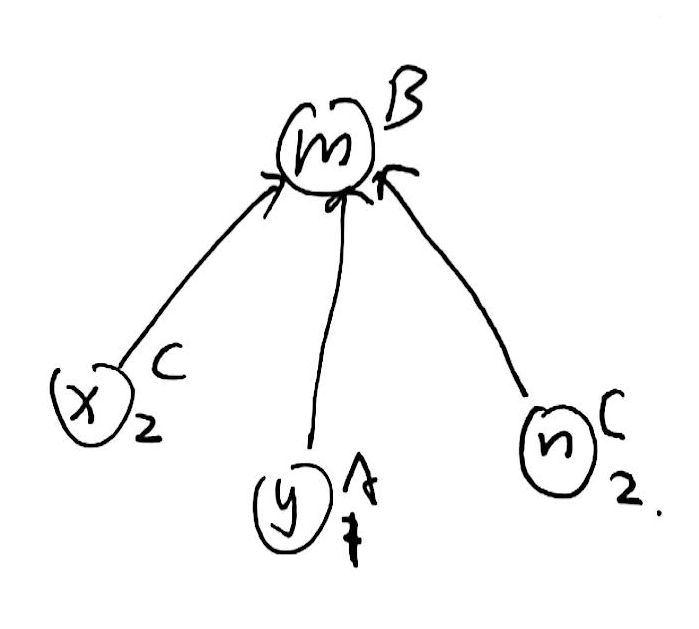
最后是求解答案时的情况： 我们假设要求解 \(A,B\) 之间的关系：

\(1-2=-1\) ？不急，\(-1\) 也是可以取模的。$(-1+3) \bmod 3 =2 $， 答案正确。

于是，我们就可以用这样的带取模的带权并查集快速的维护了。

再来一份清朝写的代码：

Show me the code

#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
	ll x=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
const int N=5e4+5;
int fa[N];
int d[N];
int _find(int u){
	if(fa[u]==u)return u;
	int t=_find(fa[u]); 
	d[u]+=d[fa[u]];
	d[u]=(d[u]+3)%3;
	fa[u]=t;
	return t;
}
int main(){
	
	int n,k;
	cin>>n>>k;
	for(int i=1;i<=n;i++){
		fa[i]=i;
		d[i]=0;
	}
	ll ans=0;
	for(int i=1;i<=k;i++){
		int t,x,y;
		cin>>t>>x>>y;
		if(x>n||y>n){
			ans++;
			continue;
		}
		else if(t==2&&x==y){
			ans++;
			continue;
		}
		int t1=_find(x),
			t2=_find(y); 
		if(t==1){
			if(t1==t2&&(d[x]-d[y]+3)%3!=0){
				ans++;
				continue;
			}
			else{
				fa[t1]=t2;
				d[t1]=d[y]-d[x];
			}
		}
		else if(t==2){
			if(t1==t2&&((d[x]-d[y]+3)%3==0||(d[x]-d[y]+3)%3==2)){
				ans++;
				continue;
			} 
			else{
				fa[t1]=t2;
				d[t1]=d[y]-d[x]+1;
			}
		}
	} 
	
	cout<<ans;
	
	
	return 0;
}

当然，只维护三种关系还是太普通了，有没有更强力一点的题目？

有的朋友，有的，请看：

题目 7 ${\color{Yellow}{\tiny 33} } $ DXJ 与四大梗王

题意简述：

背景：

• 四种竞赛：\(M, P, C, B\)。
• 玩梗关系：
  • \(M \rightarrow P\)
  • \(P \rightarrow C\)
  • \(C \rightarrow B\)
  • \(B \rightarrow M\)
• Friendship：若 \(x\) 玩 \(y\) 的梗，且 \(z\) 的梗被 \(y\) 玩，则 \(x\) 和 \(z\) 互为 friendship。例如，\(M\) 和 \(C\) 互为 friendship，\(P\) 和 \(B\) 互为 friendship。

问题：

• DXJ（\(0\) 号）想知道其他 \(N\) 个同学的竞赛类型。
• 每个同学的回答可能是以下之一：
  1. 我是 \(x\) 竞赛生。
  2. 我和 \(a\) 同学学一个竞赛。
  3. \(a\) 同学会玩我的梗。
  4. 我玩 \(a\) 同学的梗。
  5. 我与 \(a\) 同学有 friendship！

输入：

• \(N+1\) 个学生（编号 \(0 \sim N\)）。
• \(M\) 行回答。

输出：

• DXJ 与每个同学的关系（竞赛类型或 friendship）。

目标：

• 根据回答推断每个同学的竞赛类型。

---

题意简化 by deepseek

仍然考虑用并查集维护关系，这里有 \(4\) 种关系，如何安排他们的距离呢？我们从关系图上来考虑：

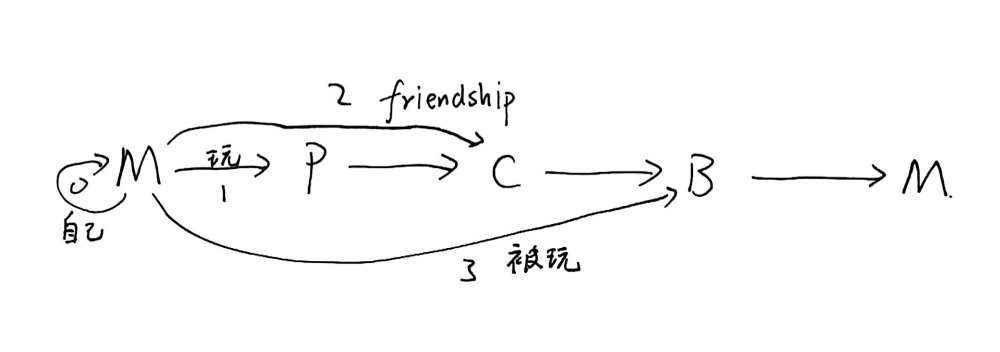
于是，我们让同种竞赛距离为 \(0\)，玩对方的距离为 \(1\)，friendship 距离为 \(2\)，被对方玩梗关系为 \(3\)，这样正确吗？

仿照题目 6 验证一下，确实是正确的。

于是这个题就做完了。

没有代码，因为数据也没有（

题目 8 异或关系

上文中我们使用带权并查集维护了加减乘除和取模关系，再来看看异或关系的维护 。

题意简述：

你没有被给定非负整数 \(x_0, x_1, \cdots, x_{n-1}\)，它们都小于 \(2^{20}\)，但它们确实存在，并且它们的值不会改变。

我会逐渐给你一些关于它们的事实，并向你提出一些问题。

有两种类型的事实，以及一种类型的问题：

• I p V 我告诉你 \(x_p =V\)
• I p q V 我告诉你 \(x_p \oplus x_q = V\)
• Q k p1 p2 ... pk 你需要输出 \(x_{p1} \oplus x_{p2} \oplus \cdots \oplus x_{pk}\) 的值。

如果你无法从我在该问题之前提供的事实中推断出特定问题的答案，则打印 I don't know.。如果第 \(i\) 个事实（不包括问题）与之前的所有事实都不一致，则打印 The first i facts are conflicting.，然后保持沉默（包括事实和问题）。在每个测试用例的输出之后打印一个空行。

维护的关系变成了异或，还能用上面的方法吗？

经过同上的验证，其实是可以的，由于异或没有方向性，公式应变为：

\[d_C \oplus d_B \oplus v=d_A \]

\[d_{B正确} =d_B \oplus d_{A正确} \]

问题在于：如何处理已知值的情况？

按照平常的思路，已知绝对值的情况是很容易处理的，但在带权并查集这个全部是相对参考系的环境中，这反而不好处理了？

既然如此，我们就在这些相对参考系中直接加入一个绝对参考系，令一个点 \(n\) 为头，特殊的是，这个点下领的所有点都是已知的，这个点的绝对值应为 \(0\)。类似与图论中的超级源点。

这样，如果我们已知一个子集中一个元素的值，这个子集中所有元素的值我们都可以知道（这一步也在懒处理中），我们就把这个子集并入以 \(n\) 开头的子集中，即可完成对已知值部分的处理。

那么，现在我们可以高高兴兴的求解 \(k\) 个数的值了吗？

注意到 \(k\) 不会很大，因此我们可以一个数一个数考虑。

如果这 \(k\) 个数都在 \(n\) 集合中，自然很好处理。

其它情况呢？我们知道异或有这样的性质：

\[x \oplus y \oplus x =y \]

我们已知点的相对关系是相对于头的关系，给出的表达式中必然带着一个头的值。

这意味着：如果有偶数个元素在同一个集合中，我们依然可以求解他们异或起来的值，但若只有奇数个，我们就无能为力了。

于是，我们把要求的数按照所属的子集分类，若存在一个子集，有奇数个元素属于它，且这个子集不是 \(n\) 子集，则此时我们将无法得到答案。若无此情况直接计算即可。

本题综合了带权并查集，超级源点，异或的性质，好题！

你说得对，但是我死活过不了这个题，输入和输出格式有点恶心，代码的主要逻辑应该是没什么问题的。

Show me the code

#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<iostream>
#include<vector>
#include<map>
#include<cstring>
#include<algorithm>
#include<string>
using namespace std;
typedef long long ll;
ll read(){
  ll x=0,f=1;
  char c=getchar();
  while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
  while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
  return x*f;
}
struct work{
  int fa;
  int v;
};
work f[50000];
int _find(int u){
  if(f[u].fa==u)return u;
  int prev=f[u].fa;
  f[u].fa=_find(f[u].fa);
  f[u].v=f[u].v^f[prev].v;
  return f[u].fa;
}
int main(){
  
  int n,q;
  int T=1;
  while(cin>>n>>q){
  	if(n==q&&n==0)break;
    for(int i=0;i<=n;i++){
      f[i].fa=i;
      f[i].v=0;
    }
    bool slit;
		getchar();
    cout<<"Case "<<T<<':'<<'\n';
    vector<int> vcc[50];
    int gccb=0;
    for(int i=1;i<=q;i++){
    	for(int j=0;j<=5;j++){
    		vcc[j].clear();
			}
      string s;
      getline(cin,s);
      if(slit==1)continue;
      if(s[0]=='I'){
        gccb++;
        int op[5];
        
        int cnt=0;
        for(int j=1;j<s.size();j++){
          if(s[j]==' ')continue;
          while(j<s.size()&&'0'<=s[j]&&s[j]<='9'){
            vcc[cnt].push_back(s[j]-'0');
            j++;
          }
          cnt++;
        }
        int cnta=0;
        for(int j=0;j<=4;j++){
          if(vcc[j].empty())break;
          int gcca=1;
          cnta++;
          for(int k=vcc[j].size()-1;k>=0;k--){
            if(k==vcc[j].size()-1){
              op[j]=vcc[j][k];
            }
            else{
              gcca*=10;
              op[j]+=vcc[j][k]*gcca;
            }
          }
        }
        if(cnta==2){
        	op[0]++;
          int t=_find(op[0]);
          if(t==0&&f[op[0]].v!=op[1]){
            cout<<"The first "<< gccb << " facts are conflicting."<<'\n';
            slit=1;
            continue;
          }
          f[t].fa=0;
          f[t].v=f[op[0]].v^op[1];
        }
        else if(cnta==3){
        	op[0]++;
        	op[1]++;
          int f1=_find(op[0]);
          int f2=_find(op[1]);
          if(f1==f2&&f[op[0]].v ^ f[op[1]].v!=op[2]){
            cout<<"The first "<< gccb << " facts are conflicting."<<'\n';
            slit=1;
            continue;
          }
          if(f1==0){
            f[f2].fa=0;
            f[f2].v=f[op[0]].v ^ f[op[1]].v ^ op[2];
          }
          else if(f2==0){
            f[f1].fa=0;
            f[f1].v=f[op[0]].v ^ f[op[1]].v ^ op[2];
          }
          else{
            f[f1].fa=f2;
            f[f1].v=f[op[0]].v ^ f[op[1]].v ^ op[2];
          }
        }
      }
      if(s[0]=='Q'){
        int op[50];
        int cnt=0;
        for(int j=1;j<s.size();j++){
          if(s[j]==' ')continue;
          while(j<s.size()&&'0'<=s[j]&&s[j]<='9'){
            vcc[cnt].push_back(s[j]-'0');
            j++;
          }
          cnt++;
        }
        int cnta=0;
        for(int j=0;j<=48;j++){
          if(vcc[j].empty())break;
          int gcca=1;
          cnta++;
          for(int k=vcc[j].size()-1;k>=0;k--){
            if(k==vcc[j].size()-1){
              op[j]=vcc[j][k];
            }
            else{
              gcca*=10;
              op[j]+=vcc[j][k]*gcca;
            }
          }
          op[j]++;
        }
        map<int,int> mp;
        for(int j=1;j<cnta;j++){
          int t=_find(op[j]);
          mp[t]++;
        }
        bool fii=0;
        for(auto v:mp){
        	//cout<<v.first<<' ';
          if(v.first!=0&&v.second%2!=0){
            cout<<"I don't know."<<'\n';
            fii=1;
            break;
          }
        }
        if(fii==1)continue;
        int ans=0;
        for(int j=1;j<cnta;j++){
          ans=ans^f[op[j]].v;
        }
        cout<<ans<<'\n';
      }
    }
    T++;
  }
  
  return 0;
}

bye~