线段树上的势能分析

前言

本文介绍了线段树问题中的一种常见题型：操作减少势能使其可以支持暴力下放操作。
本文还介绍了由吉如一神犇发明的 标签回收模型 分析暴力下放操作时间复杂度的方法，Orz。

（最近突然喜欢用罗马数字当标号）

势能分析法

势能分析法常用于分析一个数据结构的最坏时间复杂度。一般的是能分析中，我们可能通过某种操作来向数据结构中存储势能，再通过某种操作将势能释放。储存于释放两个操作的最坏时间复杂度可能不在一个量级，但是其对势能造成的变化可以求出，我们根据此来分析时间复杂度。一般地，我们将势能于整个数据结构而不是整体对象相关联。

进行势能分析时，要考虑这样两个问题：

这个数据结构的势能由谁代表？
什么样的操作会尽可能大的增加势能？
什么样的操作会尽可能小的减少势能？

在放到线段树上前，先来看几个简单的例子。

\(\mathrm{I.}\) 栈操作中的时间复杂度

假设我们初始有一个空栈，有 \(n\) 次操作，操作分别为：

\(\operatorname{PUSH}(x)\)，将一个元素压入到栈中。
\(\operatorname{POP}()\)，将一个元素从栈顶弹出。（若执行时栈空则停止整个操作）
\(\operatorname{MULTPOP(k)}\)，一次性将 \(k\) 个元素从栈顶弹出（若执行时栈空则停止整个操作）

容易发现，前两个操作的时间复杂度都是 \(O(1)\)，但是第三个操作的时间复杂度却是 \(O(k)\)。那么这 \(n\) 次操作总的时间复杂度又是多少呢？

我们如此考虑：让栈中的元素个数作为这个栈所拥有的势能，容易发现，对于每一个势能的产生与释放有 \(O(1)\) 的时间复杂度。

那么，这个栈中的势能最大值是多少呢？显然，若 \(n\) 次操作全部为 \(\operatorname{PUSH}\)，此时势能有最大值 \(n\)。那么把这 \(n\) 个势能全部放入删除等操作的最坏时间复杂度就是 \(O(n)\)。

\(\mathrm{II.}\) Dijstra 算法的时间复杂度

Dijstra 解决的是带权重的有向图上的单源最短路径问题，此算法使用贪心思想并能够使每个点做到只被访问一次，这使 Dijstra 算法的最坏时间复杂度依赖于最小有限队列的实现。

设一个带权重的有向图上的点数，边数分别为 \(n,m\) 假设我们使用一般的堆实现优先队列。令优先队列中元素的个数为算法的势能，显然的，对于每个势能的插入弹出操作的时间为 \(O(\log n)\)。

Dijstra 算法通过边访问邻接点，而每个新点的被访问又势必会让邻接的至少一条边再也不会被程序经过。综合以上可以得到 Dijstra 算法的最坏时间复杂度是 \(O((n+m)\log n)\)。在 \(n,m\) 同阶的情况下可简记为 \(O(n\log n)\)。

接下来，我们尝试在线段树上也进行一下势能分析，来看一道题：

\(\mathrm{III.}\) Libre OJ #6029.「雅礼集训 2017 Day1」市场

你有一个整数序列，请支持下面三种操作：

区间加一个数 \(a\)。

区间除以（向绝对值更小的整数取整）一个数 \(b\)（保证 \(b \ne 0\)）。

区间求和。

总共有 \(n\) 个数和 \(m\) 个操作，保证操作过程中序列中的数的绝对值的最大值小于 \(k\)（显然 \(k\ge 0\)）。

在对线段树的学习中，我们知道能在线段树上维护的信息与操作应当满足结合律，但是显然除法操作并不满足结合律，这该如何是好？

不妨来分析一下题设中除法的性质。显然，如果我们对一个数多次进行多次除数不为 \(1\) 的除法，那么这个数最后会变成 \(0\)。
而若是除以 \(1\)，元素的值不会改变。

我们还发现，如果在区间除法操作中一个节点代表的区间全部是同一个值，我们可以直接在这个点上修改而无需再往下。

这两条性质告诉我们：有没有可能在经历过海量的除法操作以后，某个区间的数全部相同，这时可以不去访问每一个值来节省时间复杂度呢？有！

既然如此，我们先尝试对所有的数暴力除法，在节点中记录区间是否全部相同的标签，若是全部相同直接修改而不再往下，能过吗？

尝试了一下发现，这种方法可以过掉题目数据范围限制下的所有随机生成的数据。但是特殊构造的数据出现了超时。

为什么呢？这需要我们来证明这个线段树的最坏时间复杂度。这里使用吉如一老师的标签回收法。

我们定义：线段树上的一个节点上有一个标签当且仅当这个节点代表的区间内的数不全部相同。
举例来说，对于下面图示的线段树，其标签分布情况如下：

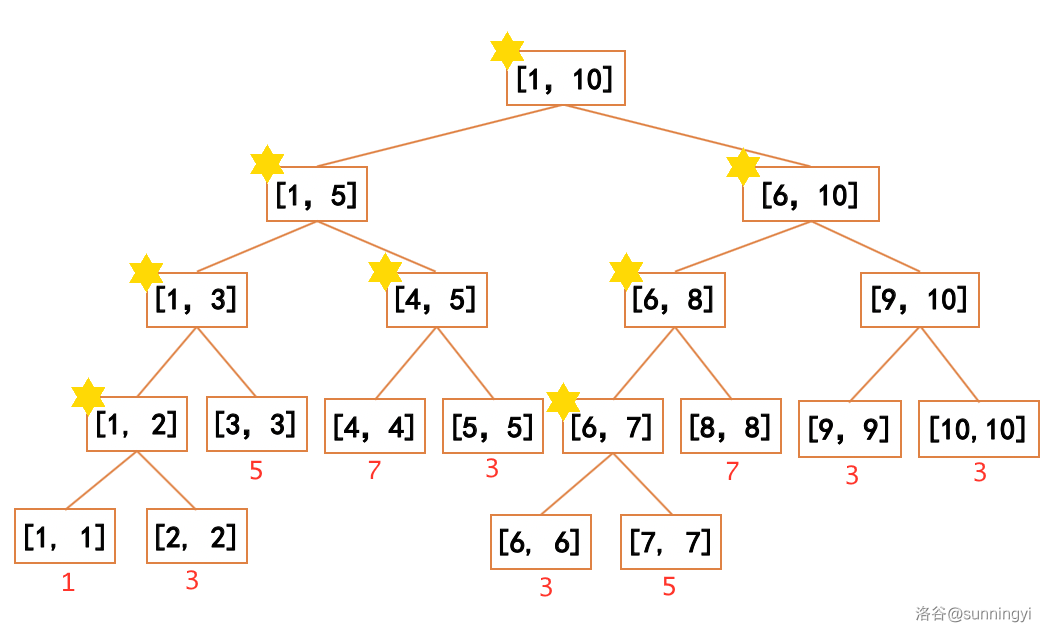
容易发现，若一个节点代表的区间内部的值全部相同，那么这个节点上就没有标记。且对这个区间整体除操作都不会再使这个节点再得到标记。

那么，我们就把一个线段树的节点中标记的数量定义为这个线段树拥有的势能。显然地，一棵线段树初始时拥有的最大势能数为 \(O(n)\) 。现在考虑，什么样的情况会减少势能呢？

要减少势能，只有通过除法和加法操作将一些数变成相同的数，显然都变成 \(0\) 是最有可能的，都变成一些非 \(0\) 的数的情况暂且不谈，因为把一些数都变成 \(0\) 有着最坏的时间复杂度，只需考虑其即可。

根据题目中的要求，把一个数变成 \(0\) 最坏的情况是对这个数进行除法操作 \(\log_2 k\) 次。若对每个值都进行 \(\log_2 k\) 次除法操作，就会让整棵线段树都是 \(0\)，此时线段树上也就没有标记了。由此我们可以得出，回收线段树上所有标记的最劣时间复杂度为 \(O(n\log _2 k)\)。平均下来，回收一个标记的时间复杂度为 \(O(\log_2 k)\)。

继续考虑，什么样的情况会增加势能呢？

首先可以知道：对一个已经全部相同的区间整体除并不会产生新的标记。标记对于每个点只有一个。

因此，增加势能仅可能由对一个区间非整体的操作导致，容易发现，若对于一个数全部相同的区间进行部分的加法（或除法）操作所可能产生的标记数量是最多的，如下图：

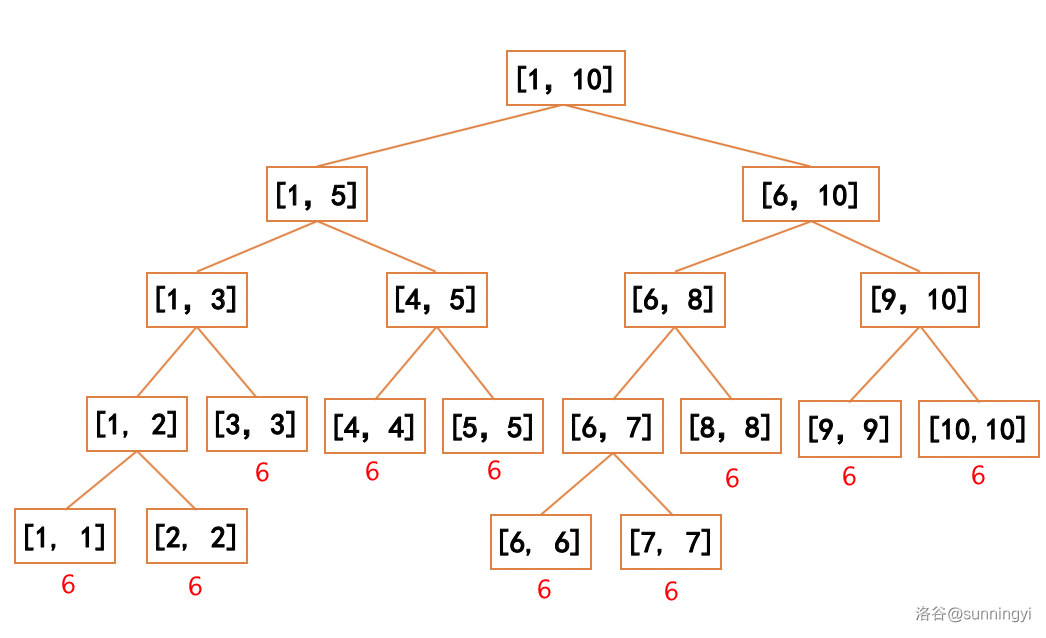
例如对区间 \([2,6]\) 除以 \(3\)：

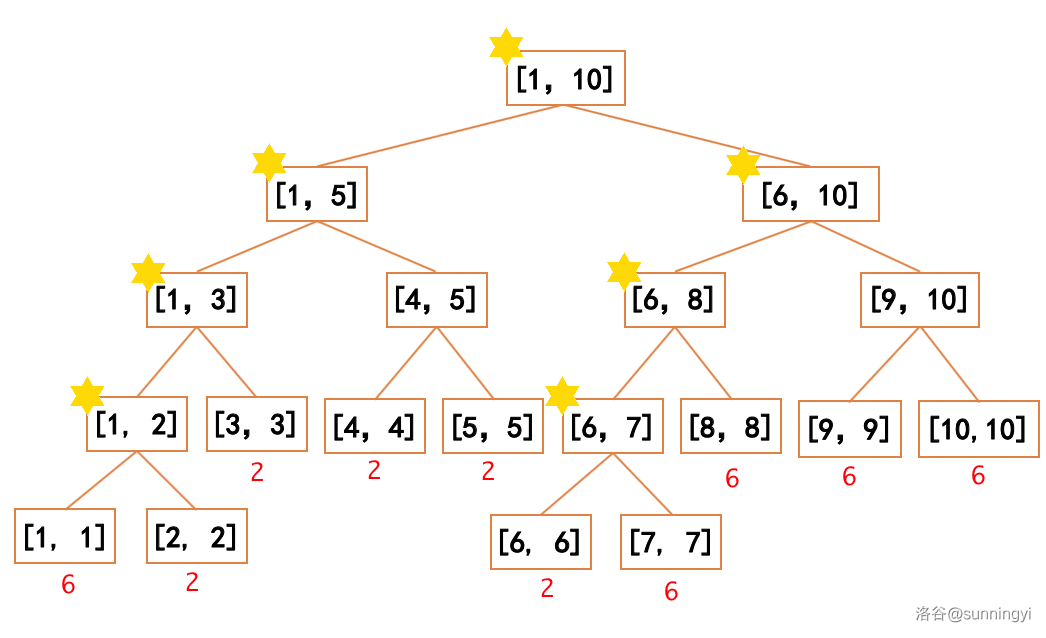
可以看到，此时标记数量增加的数量相当于两倍的树高，即 \(O(\log_2 n)\)。经过所有 \(n\) 次操作，增加的总标签数量最大为 \(O(n \log_2 n)\)（因为有标签会产生后被消除，这里也算上了被消除的）。

综合上面的分析，可以得到：线段树初始最多有 \(O(n)\) 个标签，经过 \(n\) 次操作后，最多再产生 \(O(n\log_2 n)\) 个标签，处理一个标签的时间复杂度为 \(O(\log_2 k)\)，因此这个数据结构的最劣时间复杂度为 \(O((n+n\log_2 n)\log_2 n \log_2 k)\)。平均复杂度可以记作 \(O(n\log_2 n \log_2 k)\)，由于我们分析的全部都是最劣情况，在随机数据中远远跑不到这么高的时间复杂度。

那么，什么样的数据可以卡掉我们的程序？自然是尽可能多的造标记然后清标记。例如我们可以在一个已经全部相同的区间中对一些小段加，这样就会以较少的操作数造成大量的标签产生，之后再对整个大区间进行除法，程序不得不递归深入到每个叶子进行暴力除法，再加上递归以及线段树的大常数，导致了超时。

下面是某个 hack 数据的节选，相信你一眼就能看明白原理了：

2 32 99993 4259
1 31 99986 -1
2 32 99987 4491
1 17 99956 -4906
2 2 99979 2453
1 20 99986 -5238
2 36 99990 2620
1 26 99956 -1579
2 3 99966 1581
1 4 99997 -9761
2 45 99957 1627
1 10 99993 -5838

那么怎样解决呢？我们曾经学过整除分块理论：如果一个区间内最大的和最小的数除以某个除数分别所得的商与各自被除数的变化量相等，那么区间内所有的数除以这个除数所得的商与自己的变化量一定全部相等。这意味着我们可以将对这个区间的除法操作转化为一个区间加法操作，即使这个区间内的数不全部相同，也无需再对这样的区间暴力递归下去了。

加上这个优化以后，我们轻松过掉了这题！

但是，若是细致构造数据，是可以将这个题的解法卡到平均 \(2.7s\) 的，如下面的 gen 设置：

const int N=100007;  //序列长 
const int M=100007;  //操作数 
const ll OP=1e4+7;   //除数 or 加数的最大值 
const int ADD=35000; //加法操作的数量 
const int DIV=65000; //除法操作的数量 
const int QUERYM=5;  //区间求最大值的操作的数量
                     //区间求和数量能用它们算出来

尽管如此，这个题的数据没有这么恶心。

这样，我们分析出了该方法的时间复杂度，解释了其能通过的原因，下面是代码，如果不想看可以点击右侧导航栏跳转：

代码时间

#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
  ll x=0,f=1;
  char c=getchar();
  while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
  while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
  return x*f;
}
const int N=1e5+5;
ll ori[N];
int identity=1;
struct seg{
  int l;
  int r;
  bool equ;
  ll v;
  ll minv;
  ll maxv;
  ll lzt;
}t[N*4];
void pushup(int p){
  int ls=p*2;
  int rs=p*2+1;
  t[p].v=t[ls].v+t[rs].v;
  t[p].minv=min(t[ls].minv,t[rs].minv);
  t[p].maxv=max(t[ls].maxv,t[rs].maxv);
  if(t[p].maxv==t[p].minv){t[p].equ=1;}
  else{t[p].equ=0;}
  return ;
}
ll sign(ll x) { return (x > 0) - (x < 0); }
ll divF2(ll a, ll b) { return a / b - (sign(a % b) == -sign(b)); }
void b(int p,int l,int r){
  t[p].l=l;
  t[p].r=r;
  if(l==r){
    t[p].lzt=0;
    t[p].v=ori[l];
    t[p].minv=ori[l];
    t[p].maxv=ori[l];
    t[p].equ=1;
    return ;
  }
  int mid=l+r>>1;
  b(p*2,l,mid);
  b(p*2+1,mid+1,r);
  pushup(p);

  return;
}
void pushdown(int p){
  int ls=p*2;
  int rs=p*2+1;
  ll k=t[p].lzt;
  t[p].lzt=0;
  if(t[p].equ){
    t[ls].minv=t[p].minv;
    t[ls].maxv=t[p].maxv;
    t[ls].v=1ll*(t[ls].r-t[ls].l+1)*t[p].minv;
    t[rs].minv=t[p].minv;
    t[rs].maxv=t[p].maxv;
    t[rs].v=1ll*(t[rs].r-t[rs].l+1)*t[p].minv;
    return;
  }
  t[ls].minv+=k;
  t[ls].maxv+=k;
  t[ls].v+=1ll*(t[ls].r-t[ls].l+1)*k;
  t[ls].lzt+=k;
  t[rs].minv+=k;
  t[rs].maxv+=k;
  t[rs].v+=1ll*(t[rs].r-t[rs].l+1)*k;
  t[rs].lzt+=k;
  return ;
}
void add(int p,int l,int r,ll k){
  if(l<=t[p].l&&t[p].r<=r&&t[p].equ){
    t[p].v+=1ll*(t[p].r-t[p].l+1)*k;
    t[p].minv+=k;
    t[p].maxv+=k;
    return ;
  }
  if(l<=t[p].l&&t[p].r<=r){
    t[p].v+=1ll*(t[p].r-t[p].l+1)*k;
    t[p].minv+=k;
    t[p].maxv+=k;
    t[p].lzt+=k;
    return ;
  }
  pushdown(p);
  int mid=t[p].l+t[p].r>>1;
  if(l<=mid) add(p*2,l,r,k);
  if(mid<r)  add(p*2+1,l,r,k);

  pushup(p);
  return ;
}
void div(int p,int l,int r,ll k){
  if(l<=t[p].l&&t[p].r<=r&&t[p].equ){
    ll delta=divF2(t[p].minv,k)-t[p].minv;
    t[p].v+=1ll*(t[p].r-t[p].l+1)*delta;
    t[p].minv=divF2(t[p].minv,k);
    t[p].maxv=divF2(t[p].maxv,k);
    return ;
  }
  else if(l<=t[p].l&&t[p].r<=r&&t[p].maxv-divF2(t[p].maxv,k)==t[p].minv-divF2(t[p].minv,k)){//<------小优化在这
  	ll delta=divF2(t[p].maxv,k)-t[p].maxv;
  	add(1,t[p].l,t[p].r,delta);
  	return;
	} 
  else if(t[p].l==t[p].r){
    t[p].v=divF2(t[p].v,k);
    t[p].minv=divF2(t[p].minv,k);
    t[p].maxv=divF2(t[p].maxv,k);
    return ;
  }
  pushdown(p);
  int mid=t[p].l+t[p].r>>1;
  if(l<=mid) div(p*2,l,r,k);
  if(mid<r)  div(p*2+1,l,r,k);

  pushup(p);
  return ;
}
ll qmin(int p,int l,int r){
  if(l<=t[p].l&&t[p].r<=r){
    return t[p].minv;
  }
  pushdown(p);
  int mid=t[p].l+t[p].r>>1;
  ll mri=LONG_LONG_MAX;
  if(l<=mid) mri=min(mri,qmin(p*2,l,r));
  if(mid<r)  mri=min(mri,qmin(p*2+1,l,r));

  return mri;
} 
ll qsum(int p,int l,int r){
  if(l<=t[p].l&&t[p].r<=r){
    return t[p].v;
  }
  pushdown(p);
  int mid=t[p].l+t[p].r>>1;
  ll mri=0;
  if(l<=mid) mri+=qsum(p*2,l,r);
  if(mid<r)  mri+=qsum(p*2+1,l,r);

  return mri;
} 
int main(){

  int n,q;
  cin>>n>>q;
  rep(i,1,n){
    cin>>ori[i];
  }
  b(1,1,n);
  for(;identity<=q;identity++){
    int op;
    cin>>op;
    if(op==1){
      ll l,r,k;
      cin>>l>>r>>k;l++;r++;
      add(1,l,r,k);
    }
    else if(op==2){
      ll l,r,k;
      cin>>l>>r>>k;l++;r++;
      div(1,l,r,k);
    }
    else if(op==3){
      ll l,r;
      cin>>l>>r;l++;r++;
      cout<<qmin(1,l,r)<<'\n';
    }
    else if(op==4){
      ll l,r;
      cin>>l>>r;l++;r++;
      cout<<qsum(1,l,r)<<'\n';
    }
  }
  
  return 0;
}

\(\mathrm{IV.}\) Codeforces 438 D

你有一个整数序列，请支持下面三种操作：

单点加一个数 \(a\)。

区间取模一个数 \(b\)（保证 \(b > 0\)）。

区间求和。

总共有 \(n\) 个数和 \(m\) 个操作，保证操作过程中序列中的数的绝对值的最大值小于 \(k\)（显然 \(m\ge 0\)）。

其实如果分析一下取模的性质，可以发现它也像除法一样每次取模不为 \(1\) 的数至少减半，然后就和 \(\mathrm{III}\) 中的解法没区别了。类似的还有区间开方操作等。

本题的时限 \(4s\) 但是数据好像不强，下面的代码只跑了 \(1046ms\)。如果不想看可以点击右侧导航栏跳转：

代码时间

#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define NOSM -1
ll read(){
  ll x=0,f=1;
  char c=getchar();
  while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
  while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
  return x*f;
}
const int N=1e5+5;
ll ori[N];
struct seg{
  int l;int r;bool equ;
  ll v;ll minv;ll semv;ll maxv;ll lzt;
}t[N*4];
void pushup(int p){
  int ls=p*2;
  int rs=p*2+1;
  t[p].v=t[ls].v+t[rs].v;
  t[p].minv=min(t[ls].minv,t[rs].minv);
  t[p].maxv=max(t[ls].maxv,t[rs].maxv);
  if(t[p].maxv==t[p].minv){
    t[p].equ=1;
    t[p].semv=NOSM;
  }
  else if(t[p].maxv==t[ls].maxv){
    t[p].semv=max(t[ls].semv,t[rs].maxv);
    t[p].equ=0;
  }
  else{
    t[p].semv=max(t[ls].maxv,t[rs].semv);
    t[p].equ=0;
  }
  return ;
}
void b(int p,int l,int r){
  t[p].l=l;
  t[p].r=r;
  if(l==r){
    t[p].lzt=0;
    t[p].v=ori[l];
    t[p].minv=ori[l];
    t[p].maxv=ori[l];
    t[p].equ=1;
    return ;
  }
  int mid=l+r>>1;
  b(p*2,l,mid);
  b(p*2+1,mid+1,r);
  pushup(p);

  return;
}
void pushdown(int p){
  int ls=p*2;
  int rs=p*2+1;
  ll k=t[p].lzt;
  t[p].lzt=0;
  if(t[p].equ){
    t[ls].minv=t[p].minv;
    t[ls].maxv=t[p].maxv;
    t[ls].v=1ll*(t[ls].r-t[ls].l+1)*t[p].minv;
    t[rs].minv=t[p].minv;
    t[rs].maxv=t[p].maxv;
    t[rs].v=1ll*(t[rs].r-t[rs].l+1)*t[p].minv;
    return;
  }
  t[ls].minv+=k;
  t[ls].maxv+=k;
  t[ls].v+=1ll*(t[ls].r-t[ls].l+1)*k;
  t[ls].lzt+=k;
  t[rs].minv+=k;
  t[rs].maxv+=k;
  t[rs].v+=1ll*(t[rs].r-t[rs].l+1)*k;
  t[rs].lzt+=k;
  return ;
}
void add(int p,int l,int r,ll k){
  if(l<=t[p].l&&t[p].r<=r&&t[p].equ){
    t[p].v=1ll*(t[p].r-t[p].l+1)*k;
    t[p].minv=k;
    t[p].maxv=k;
    return ;
  }
  if(l<=t[p].l&&t[p].r<=r){
    t[p].v+=1ll*(t[p].r-t[p].l+1)*k;
    t[p].minv+=k;
    t[p].maxv+=k;
    t[p].lzt+=k;
    return ;
  }
  pushdown(p);
  int mid=t[p].l+t[p].r>>1;
  if(l<=mid) add(p*2,l,r,k);
  if(mid<r)  add(p*2+1,l,r,k);

  pushup(p);
  return ;
}
void moudulo(int p,int l,int r,ll k){
  if(t[p].maxv<k)return;
  if(l<=t[p].l&&t[p].r<=r&&t[p].equ){
    ll delta=t[p].maxv%k-t[p].maxv;
    t[p].v+=1ll*(t[p].r-t[p].l+1)*delta;
    t[p].minv=t[p].minv%k;
    t[p].maxv=t[p].maxv%k;
    return ;
  }
  pushdown(p);
  int mid=t[p].l+t[p].r>>1;
  if(l<=mid) moudulo(p*2,l,r,k);
  if(mid<r)  moudulo(p*2+1,l,r,k);

  pushup(p);
  return ;
}
ll qsum(int p,int l,int r){
  if(l<=t[p].l&&t[p].r<=r){
    return t[p].v;
  }
  pushdown(p);
  int mid=t[p].l+t[p].r>>1;
  ll mri=0;
  if(l<=mid) mri+=qsum(p*2,l,r);
  if(mid<r)  mri+=qsum(p*2+1,l,r);

  return mri;
} 
int main(){

  int n,q;
  cin>>n>>q;
  rep(i,1,n){
    cin>>ori[i];
  }
  b(1,1,n);
  for(int i=1;i<=q;i++){
    int op;
    cin>>op;
    if(op==3){
      ll p,k;
      cin>>p>>k;
      add(1,p,p,k);
    }
    else if(op==2){
      ll l,r,k;
      cin>>l>>r>>k;
      moudulo(1,l,r,k);
    }
    else if(op==1){
      ll l,r;
      cin>>l>>r;
      cout<<qsum(1,l,r)<<'\n';
    }
  }
  
  return 0;
}

\(\mathrm{V.}\) 区间取较小/大值

给出一个长度为 \(n\) 的数列 \(A\)。接下来进行了 \(m\) 次操作，操作有五种类型，按以下格式给出：

1 l r k：对于所有的 \(i\in[l,r]\)，将 \(A_i\) 加上 \(k\)（\(k\) 可以为负数）。

2 l r v：对于所有的 \(i\in[l,r]\)，将 \(A_i\) 变成 \(\min(A_i,v)\)。

3 l r：求 \(\sum_{i=l}^{r}A_i\)。

4 l r：对于所有的 \(i\in[l,r]\)，求 \(A_i\) 的最大值。

我们自然想到把区间取 min 向下暴力操作。

但是，如果直接暴力操作，时间复杂度是难以承受的，这个的原因在下面解释。

解决方法是：对于这棵线段树，我们除了记录一个区间的最大值，还记录这个区间的严格次大值。一个显然的优化是：如果一个取 min 操作到了一个点，这个点代表的区间的最大值大于 \(k\)，但是次大值就小于等于 \(k\)，此时我们只需要操纵最大值即可（具体实现看后面w）。

为此，我们把懒标记设置为两个：最大值懒标记与其他值懒标记。当遇到上面的情况时仅修改最大值懒标记。

现在，我们使用标签回收势能分析法分析时间复杂度。

我们定义：线段树上的一个点有标签当且仅当其所代表区间的最大值与父亲所代表区间的最大值不同。

容易得到：一棵线段树初始最多有 \(O(n)\) 个标签。

接下来分析标签何时消失：

如果通过加法操作让标签消失显然不太可能，这里只考虑区间取 min 的贡献。在递归暴力取 min 的时候，如果一个点同意取 min 操作继续向下递归进行，可以发现：这个点的子节点上一定有标记，且这个标记经过这个操作一定会被回收。

为什么？原因是我们同意在点代表的区间已经属于目标区间的情况下还继续向下暴力取 min 的条件是值 \(k\) 比区间最大值，次大值都要小。那么操作完以后左右的最大值都相同了，那个子节点上的标记自然也没了。

这里对应解释了直接暴力操作不可行的原因：如果一个节点代表的区间的最大值大于 \(k\)，但是次大值就小于等于 \(k\)，且其一个儿子有标记，此时允许下放，显然处理完成后有标记的儿子依然有标记，这导致回收标记的时间复杂度不再是 \(O(\log_2 n)\)，而是变得不可控了。

于是优化后的回收标签的时间复杂度为 \(O(\log_2 n)\)。

接下来分析标签何时产生。

如同我们在 \(\mathrm{III}\) 中分析的那样，标签的产生在一次操作中最多只会产生 \(O(\log_2 n)\) 个。

于是可以得出时间复杂度为 \(O((n+n\log_2 n)\log_2^2n)\)，由于标签产生的数量远小于 \(O(n\log_2 n)\)，复杂度可视作 \(O(n\log_2^2n)\)。

吉如一老师自己承认了在论文中证明的 \(O(n\log_2 n)\) 时间复杂度是伪证，若综合考虑线段树的常数等问题，在实测中的耗时更接近 \(O(n\log_2^2n)\)。

关于吉老师的线段树戳这里。

posted @ 2025-02-21 20:51 hm2ns 阅读(177) 评论(0) 收藏举报

刷新页面返回顶部

hm2nsite

不过总有一天，我的心会游过夜晚，游到走累的你的身边

线段树上的势能分析

前言

势能分析法

\(\mathrm{I.}\) 栈操作中的时间复杂度

\(\mathrm{II.}\) Dijstra 算法的时间复杂度

\(\mathrm{III.}\) Libre OJ #6029.「雅礼集训 2017 Day1」市场

代码时间

\(\mathrm{IV.}\) Codeforces 438 D

代码时间

\(\mathrm{V.}\) 区间取较小/大值

公告