差分约束
前言
事情的起因:
于是滚回来补习了。
1. 是什么
差分约束是一种图论建模技巧,可以处理一个二元一次不等式组的可行解。使用差分约束算法可以在 \(O(nm)\) 的时间内求出所有变量的一组可行解,(满足题目要求的)最小解,最大解,所有解的最小值和所有解的最大值。
什么是二元一次不等式组呢?它长这样:
让你求它的一组可行解。
我们先把它移个项:
这和图论有什么关系?
来回忆我们学的最短路知识:对于下面这个很简单的有向图的一个部分:
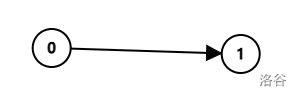
假设我们已经求解出来了节点 \(0,1\) 的最短路,设为 \(d_0,d_1\),设这两点的边权为 \(w\),显然一定有:
为什么?\(d_1= d_0+w\) 代表 \(1\) 的最短路就是由 \(0\) 更新而来的,而 \(d_1<d_0+w\) 代表 \(1\) 的最短路是由连接 \(1\) 的其它节点更新而来的,两者一结合就是我们上面的不等式。
欸?这是不是和我们的那些不等式组长得一样?于是我们可以建边了!
拿板子题举例子吧:P5960 【模板】差分约束
首先对于所有输入都从 \(x_{c'_i}\) 向 \(x_{c_i}\) 连一条边权为 \(y_i\) 的有向边。
此时可能不等式之间会构成多个不同的连通块,于是我们用一个超级源点向每一个节点连一条边权为 \(0\) 的边,这样就可以只用从超级源点开始跑最短路了。
你可能会问,我们要求最短路,这样用超级源点不会影响答案吗?
显然不会,如果题目中要求两个变量之间的差值小于一个正数,那么显然两个变量都赋 \(0\) 也是一种合法的解。
而且题目中还会出现差值是负数的情况,这就交给最短路算法解决就可以了。
显然我们的最短路算法要用 spfa,但是你先别似。
这里的超级源点还有一个作用:限制每一个变量的最大值,为什么应该很显然吧。
那么如果题目的情况无解该如何判断呢?
显然如果无解那么它们应该构成一个负环,如图:
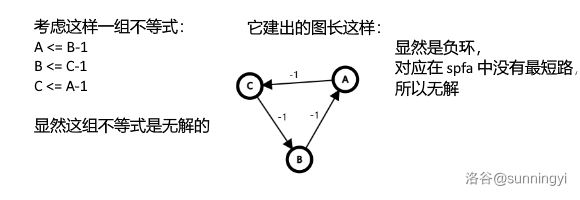
于是我们熟练地写出 spfa,成功通过模板题。
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=5e3+5;
struct e{
int v;
int w;
};
vector<e> edge[N];
bool vis[N];
int dist[N];
int cnt[N];
bool undef=0;
int n,m;
void spfa(int s){
memset(dist,0x3f,sizeof dist);//求最短路
queue<int> q;
q.push(s);
dist[s]=0;
cnt[s]=0;
vis[s]=1;
while(q.size()){
int u=q.front();
vis[u]=0;
q.pop();
for(int i=0;i<edge[u].size();i++){
int v=edge[u][i].v;
int w=edge[u][i].w;
if(dist[v]>dist[u]+w){
dist[v]=dist[u]+w;
cnt[v]=cnt[u]+1;
if(cnt[v]>n+1){//判负环,也就是无解
undef=1;
return;
}
else if(!vis[v]){
vis[v]=1;
q.push(v);
}
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
edge[v].push_back(e{u,w});
}
for(int i=1;i<=n;i++){
edge[0].push_back(e{i,0});
}
spfa(0);
if(undef){
cout<<"NO";
}
else{
for(int i=1;i<=n;i++){
cout<<dist[i]<<' ';
}
}
return 0;
}
你可能还会问:不是说了最大解也可以求吗?如果求最大解?
先想想我们求最长路后两点之间会满足什么不等式:
假设我们已经求解出来了节点 \(0,1\) 的最长路,设为 \(d_0,d_1\),设这两点的边权为 \(w\),显然一定有:
我们能把题目要求的式子变成这样吗?显然可以,下文为了方便只举不等式组中的一例:
真不错,建边的方法我们也有了:
首先对于所有输入都从 \(x_{c_i}\) 向 \(x_{c'_i}\) 连一条边权为 \(-y_i\) 的有向边。
然后超级源点连边权为 \(0\) 的边。
之后从超级源点开始跑一边最长路即可。
这里超级源点的作用就变成了限制每个变量的最小值。
这里不等式组无解的条件就变成了图中有正环。
依然可以通过模板题:
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=5e3+5;
struct e{
int v;
int w;
};
vector<e> edge[N];
bool vis[N];
int dist[N];
int cnt[N];
bool undef=0;
int n,m;
void spfa(int s){
memset(dist,-0x3f,sizeof dist);//最长路
queue<int> q;
q.push(s);
dist[s]=0;
cnt[s]=0;
vis[s]=1;
while(q.size()){
int u=q.front();
vis[u]=0;
q.pop();
for(int i=0;i<edge[u].size();i++){
int v=edge[u][i].v;
int w=edge[u][i].w;
if(dist[v]<dist[u]+w){
dist[v]=dist[u]+w;
cnt[v]=cnt[u]+1;
if(cnt[v]>n+1){
undef=1;
return;
}
else if(!vis[v]){
vis[v]=1;
q.push(v);
}
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
edge[u].push_back(e{v,-w});//建边的过程要注意
}
for(int i=1;i<=n;i++){
edge[0].push_back(e{i,0});
}
spfa(0);
if(undef){
cout<<"NO";
}
else{
for(int i=1;i<=n;i++){
cout<<dist[i]<<' ';
}
}
return 0;
}
2. 怎么用
再来一道题练练手吧 P3275 [SCOI2011] 糖果;
当然这题正解并不是用 spfa 实现的差分约束,但是 spfa 依然可以 AC,靠rp
我们先讲如何将题目抽象成差分约束问题。
显然这个题让我们求解在满足所有约束条件下的每个变量和的最小值。
首先摆结论:当题目要求和最小就跑最长路,和最大就跑最短路。
听起来好像有些反直觉,我们看看这两种情况的公式:
对于最大值:
显然这时候对于每个 \(d_1\),也就是每个变量的值,一定有一个最小值,此时我们才跑最长路。
对于最小值:
显然这时候对于每个 \(d_1\),也就是每个变量的值,一定有一个最大值,此时我们才跑最短路。
于是对于这个题目,我们要跑最长路,就要把题目中给的限制转换成用大于等于号连接的形式。
一点点看题目中给的条件:
- 如果 \(X=1\), 表示第 \(A\) 个小朋友分到的糖果必须和第 \(B\) 个小朋友分到的糖果一样多;
(好像是这题最难处理的条件了,如果以前不知道好像根本无从下手,也可能是我太菜了)
也就是要求 \(A=B\)。
其实和 \(A\ge B,B\ge A\) 是等价的。
于是就从 \(A\) 向 \(B\),从 \(B\) 向 \(A\) 分别建一条边权为 \(0\) 的有向边就可以了。
- 如果 \(X=2\), 表示第 \(A\) 个小朋友分到的糖果必须少于第 \(B\) 个小朋友分到的糖果;
也就是 \(A<B\)。
等价于 \(A+1\le B\)。
于是有 \(B\ge A+1\)。
从 \(A\) 向 \(B\) 建一条边权为 \(1\) 的有向边就可以了。
- 如果 \(X=3\), 表示第 \(A\) 个小朋友分到的糖果必须不少于第 \(B\) 个小朋友分到的糖果;
也就是 \(A\ge B\)。
从 \(B\) 向 \(A\) 建一条边权为 \(0\) 的有向边就可以了。
- 如果 \(X=4\), 表示第 \(A\) 个小朋友分到的糖果必须多于第 \(B\) 个小朋友分到的糖果;
也就是 \(A>B\)。
等价于 \(A\ge B+1\)。
从 \(B\) 向 \(A\) 建一条边权为 \(1\) 的有向边就可以了。
- 如果 \(X=5\), 表示第 \(A\) 个小朋友分到的糖果必须不多于第 \(B\) 个小朋友分到的糖果;
也就是 \(A\le B\)。
等价于 \(B\ge A\)。
从 \(A\) 向 \(B\) 建一条边权为 \(0\) 的有向边就可以了。
于是建边处理完了,超级源点呢?
在最长路问题中,超级源点向其它点的边权限制每个点的最小值。
题目中对最小值有要求吗?
注意到这一句话:
要求每个小朋友都要分到糖果
意味着题目限制最小值为 \(1\)。
于是从超级源点向每个点连一条权值为 \(1\) 的边,跑最长路即可。
但是这么做会 T,因为原题的数据是
对于 \(100\%\) 的数据,保证 \(N\leq100000,K\leq100000\)
\(N,K\) 乘起来一定会炸的。
但是我们可以充分发挥人类智慧,给 spfa 添加一个循环次数限制,如果超过了循环次数限制,自动认为无解,我们猜一个上限,多交几遍试试。
然而作者一遍就猜对了。。。
AC 代码:
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=5e5+5;
struct e{
int v;
ll w;
};
vector<e> edge[N];
ll dist[N];
bool vis[N];
int cnt[N];
int n,k;
bool cc=0;
void spfa(int s){
queue<int> q;
q.push(s);
vis[s]=1;
cnt[s]=0;
memset(dist,-0x3f,sizeof dist);//最长路
dist[s]=0;
int tot=0;//spfa 次数限制
while(q.size()){
tot++;
if(tot>1e7){
cc=1;
cout<<-1;
return;
}
int u=q.front();
q.pop();
vis[u]=0;
for(int i=0;i<edge[u].size();i++){
int v=edge[u][i].v;
ll w=edge[u][i].w;
if(dist[v]<dist[u]+w){
dist[v]=dist[u]+w;
cnt[v]=cnt[u]+1;
if(cnt[v]>n){
cc=1;
cout<<-1;
return;
}
if(!vis[v]){
vis[v]=1;
q.push(v);
}
}
}
}
}
int main(){
cin>>n>>k;
for(int i=1;i<=k;i++){
int x,a,b;
cin>>x>>a>>b;
if(x==1){//建边千万千万不能搞错不然有苦说不出
edge[a].push_back(e{b,0});
edge[b].push_back(e{a,0});
}
else if(x==2){
edge[a].push_back(e{b,1});
}
else if(x==3){
edge[b].push_back(e{a,0});
}
else if(x==4){
edge[b].push_back(e{a,1});
}
else if(x==5){
edge[a].push_back(e{b,0});
}
}
for(int i=1;i<=n;i++){
edge[0].push_back(e{i,1});
}
spfa(0);
if(cc)return 0;
ll ans=0;
for(int i=1;i<=n;i++){
// cout<<dist[i]<<' ';
ans+=dist[i];
}
cout<<ans;
return 0;
}
当然我猜你一定很想知道正解是什么。
发现我们建的边边权只有 \(0,1\),有向图还有个什么有名的算法来着?
没错是缩点。
我们先把所有边建好图,先来一波缩点。
然后我们找每个 SCC 中是否存在一条及以上的边权为 \(1\) 的边。
如果存在,意味着这条边可以被多次经过,也就是正环,此时无解。
如果没有,此时边权为 \(1\) 的边一定连接着两个 SCC,此时根据我们的建图,这两个 SCC 的取值,前面的(指引出这条有向边的)SCC 的值一定小于后面的。
而如果某些 SCC 的入度为 \(0\),代表这些 SCC 中的点没有额外的限制,因为要求最小值,我们贪心的设这些 SCC 中的点的值全部为 \(1\)。
我们从入度为 \(0\) 的点开始拓扑排序,求解出对于每个 SCC,其被要求的需要满足的最大值是多少。为了贪心,对于任意一个 SCC,如果其最大值为 \(k\),那么它要求下一个 SCC 满足的值应是 \(k+1\)。最大值是多少,里面的点就应该赋成多少,然后加上就是答案了。
也不是很难写,就不放代码了,事实是我没写过。
bye~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号