Splay 树
前言
不如 Fhq Treap
由我们的老熟人 Tarjan 巨佬发明的数据结构,CCCCOrz
1. 原理
Splay 也是一种平衡树,与 Treap 一类数据结构不同的是,它摒弃了玄学随机数维护平衡的方法,而是使用旋转的操作维护整棵树的平衡。当然,旋转操作也与 Treap 有很大的不同。
Splay 同样可以维护区间信息,但评价是不如 Fhq Treap。
我们先说维护全局信息的 Splay,这里的 Splay 满足左子树值小于树根值小于右子树值的性质。
Splay 也是一种动态开点树,对值域较大的数据无须离散化。
还是用万年不变的例题P3369 【模板】普通平衡树。
首先来说说 struct 怎么写
struct splay{
int ls;
int rs;
int var;
int sizet;
int cnt;
}spl[N];
int idx,root;
int ls int rs 代表 Splay 上这个节点存储的左儿子和右儿子;int var 代表这个节点的值;int sizet 表示这个节点领导的子树的大小,int cnt 表示和值为 var 的数出现的次数(这个节点重复了多少次)。
全局变量 int idx 记录开点的编号,int root 记录当前 Splay 的根节点。
创建一个点 & 更新子树大小
创建一个节点是在进行插入点操作时发现没有目标节点的时候进行的操作,因此这里使用引用传参来在开点的同时给 Splay 的儿子也赋上值。
更新子树大小时要加上的还有自己点的 cnt。
void newnode(int &p,int &var){
p=++idx;
spl[p].var=var;
spl[p].sizet=1;
spl[p].cnt=1;
}
void update(int p){
spl[p].sizet=spl[spl[p].ls].sizet+spl[spl[p].rs].sizet+spl[p].cnt;
}
旋转操作
和 Treap 相同,Splay 也有左旋右旋操作,定义和 Treap 相同,这里再写一遍吧。
右旋 zig
有口诀:右旋拎左右挂左。
什么意思呢,来看图解:
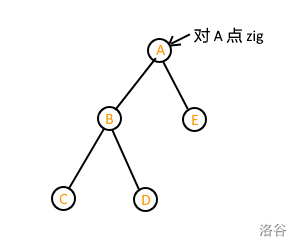
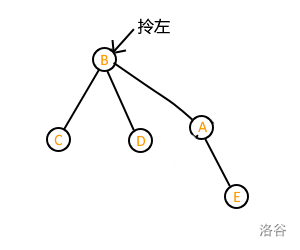
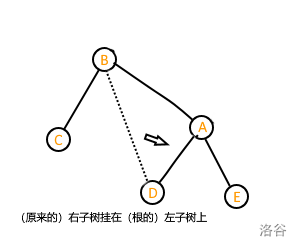
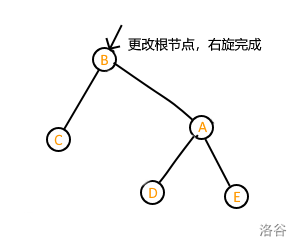
可以发现,进行完旋转操作后各个节点之间的大小关系均不变。
下面是代码,依然使用引用传参便于操作:
void zig(int &now){//右旋
int l=spl[now].ls;//拎左
spl[now].ls=spl[l].rs;//右挂左
spl[l].rs=now;//自己变成左边的右儿子
now=l;//更新根的值
update(spl[now].rs);//更新子树大小
update(now);
}
左旋 zag
有口诀:左旋拎右左挂右。
和右旋一样,就不放图了。
可以发现,进行完旋转操作后各个节点之间的大小关系均不变。
void zag(int &now){//左旋
int r=spl[now].rs;//拎右
spl[now].rs=spl[r].ls;//左挂右
spl[r].ls=now;//自己变成右边的左儿子
now=r;//更新根的值
update(spl[now].ls);//更新子树大小
update(now);
}
双旋操作
我们不想让 Splay 出现长长的链,这时候就要用到双旋操作来让 Splay 上长长的链少一点。
zig zig 操作
考虑这种情况:我们要把节点 \(C\) 变成根节点。
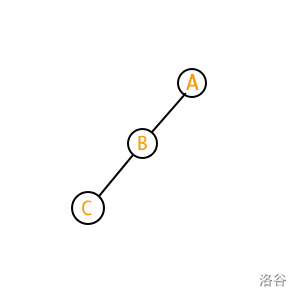
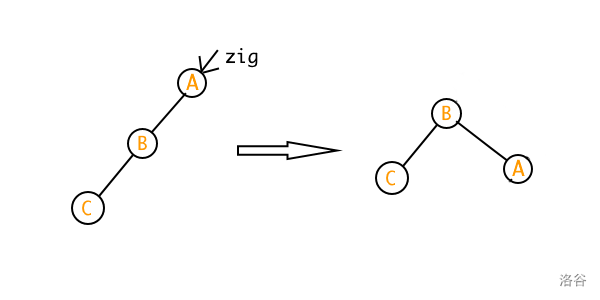
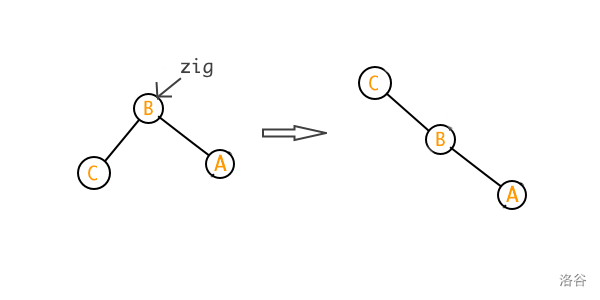
我们的目标成功完成。
zag zag 操作
其实就是 zig zig 反过来,不再放图了,其实是懒。
那你可能会问,这不还是两个链?
你先别急
zig zag 操作
考虑这样的情况,我们还是要让 \(C\) 点变成根:
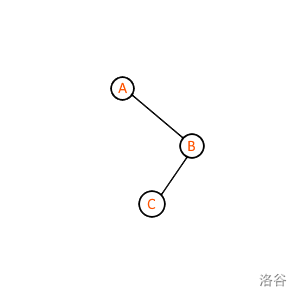
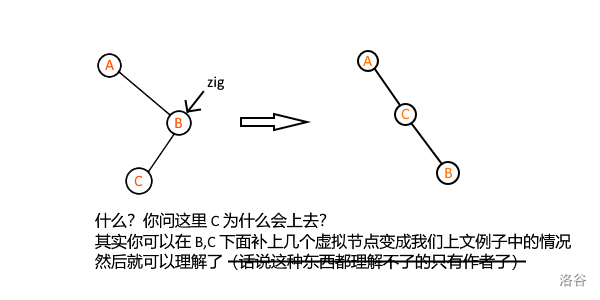
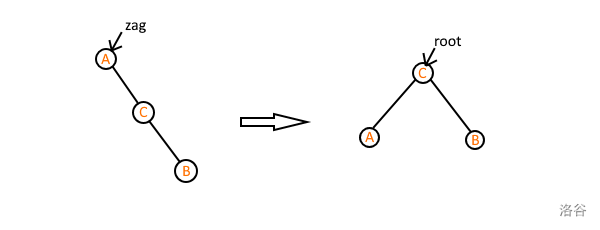
于是我们解决了问题。
zag zig 操作
就是对这三个点组成的大于号进行旋转的过程,正好和上面反过来,不再放图了。
综合上面六种操作,我们可以写出一个递归版本的 splaying(int x,int &y) 表示把节点 \(x\) 通过旋转放到 \(y\) 的位置。
操作大概是这样
首先由于我们的 Splay 是按照值的大小决定左儿子右儿子的,因此我们可以很方便的根据值的大小判断这个节点再某个节点的左子树区域还是右子树区域
我们的旋转操作一定是让目标节点旋转到当前的根节点并成为根节点,因此我们先从根节点开始考虑(也就是说 \(y=\) 根节点)。
如果 \(x\) 就是 \(y\) 的左儿子,那么只需要对 \(y\) 做一次右旋就可以把 \(x\) 转到 \(y\) 的位置去了,直接调用一次 zig 函数即可。
如果 \(x\) 就是 \(y\) 的右儿子。对 \(y\) 进行一次右旋即可。
如果这两种情况都不满足,那么就一定是双旋操作了,考虑把整个大问题拆分成子问题:
如果 \(x\) 位于 \(y\) 的左儿子的左子树区域,只需要把 \(x\) 旋转到 \(y\) 的左儿子的左儿子的位置,然后就是一个 zig zig 操作就可以把 \(x\) 移到根上去。
如果 \(x\) 位于 \(y\) 的左儿子的右子树区域,只需要把 \(x\) 旋转到 \(y\) 的左儿子的右儿子的位置,然后就是一个 zag zig 操作。
......
剩下的两种操作就不写了,你肯定能自己想到了。
另外,在进行这四种操作之前一定要特判一下,如果两个点是同一个点,那么直接返回就可以了。
由于左旋右旋以及它们的组合即都会涉及到左儿子右儿子和根的变换,因此使用引用传参方便一下操作。
以下是代码,注释很详细:
void splaying(int x,int &y){
if(x==y){//开始前的特判,相等了直接返回
return;
}
int &l=spl[y].ls,&r=spl[y].rs;//把左右节点能成一个字母的变量方便操作,当然也要用引用传参
if(x==l){//就是目标节点的左儿子,直接做一次右旋就可以了。
zig(y);
}
else if(x==r){//是右儿子,直接做一次左旋就可以了。
zag(y);
}
else{//两种都不符合那么一定是双旋操作了
if(spl[x].var<spl[y].var){//如果当前节点在目标节点的左子树位置
if(spl[x].var<spl[l].var){//如果在目标节点左儿子的左子树位置
splaying(x,spl[l].ls);//只需要把 x 旋转到目标节点左儿子的左儿子的位置
zig(y);//做两次右旋就可以了
zig(y);
}
else{//如果不符合上面的就一定是在目标节点左儿子的右子树位置
splaying(x,spl[l].rs);//只需要把 x 旋转到目标节点左儿子的右儿子的位置
zag(l);//做 zag-zig 就可以了
zig(y);
}
}
else{
if(spl[x].var>spl[r].var){//如果当前节点在目标节点的右子树位置
splaying(x,spl[r].rs);//只需要把 x 旋转到目标节点右儿子的右儿子的位置
zag(y);//做两次左旋就可以了
zag(y);
}
else{//如果不符合上面的就一定是在目标节点右儿子的左子树位置
splaying(x,spl[r].ls);//只需要把 x 旋转到目标节点右儿子的左儿子的位置
zig(r);//做 zig-zag 就可以了
zag(y);
}
}
}
}
加入点操作
设要插入的点的值是 \(var\)。
首先我们要根据二叉搜索树的特性找到 \(var\) 应该在的位置。
如果在这之前 \(var\) 已经存在,把这个点的重复次数加一,然后更新这个子树的大小。
如果不存在,新开一个点。
无论上面是什么情况,为了防止树退化成链,总是要把上面操作过的点旋转到根的位置并更新根的值。
注意可能会对某些点的左右儿子和自己产生影响,要用引用传参。
void add(int &p,int &var){
if(!p){//没出现过
newnode(p,var);//新建一个
splaying(p,root);//转到根去
return ;
}
if(var<spl[p].var){//往左找
add(spl[p].ls,var);
}
else if(var>spl[p].var){//往右找
add(spl[p].rs,var);
}
else{//出现过了
spl[p].sizet++;//更新树的大小和出现次数
spl[p].cnt++;
splaying(p,root);//扔到根去
}
}
删除点操作
删除操作有点复杂,设当前要删除的值为 \(var\)。
第一步还是找到要删除的点的位置,然后不管怎么样先把这个点扔到根节点的位置。
然后如果这个点在之前的出现次数大于 \(1\),这很好办,直接把出现次数减一就好了,也要更新一下树的大小。
如果这个点的出现次数正好为一,也就是说这个点要没了,此时为了维护二叉搜索树的特性,要选一个新的节点取代要删除的点的位置。
选谁呢?是 \(var\) 的后继,也就是比 \(var\) 大的数中最小的那一个。
找后继很简单,在现在的右子树中找就可以了,\(var\) 现在可是根节点。
然后我们把找到的后继旋转到根节点的右儿子的位置。
此时来想想 "根节点的右儿子的左儿子" 应该是什么?很明显没有东西,根据二叉搜索树的性质应该很好理解吧。
于是我们可以顺理成章的让当前根节点的左儿子变成当前节点的右儿子的左儿子,然后把根节点的指针指向当前节点的右儿子,这样根节点,也就是 \(var\),成功被抛弃掉了,我们也成功完成了删除操作。
当然,如果 \(var\) 没有后继,直接让它的左儿子当根就好了。
如果你没有看懂,那就自己模拟一下试试吧。
代码:
void del(int p,int var){
if(spl[p].var==var){//找到了
splaying(p,root);//二话不说先转到根节点
if(spl[p].cnt>1){//出现次数大于1 很好办了
spl[p].cnt--;
spl[p].sizet--;
return;
}
if(spl[p].rs!=0){//要删除这个点,且这个点有后继
p=spl[p].rs;
while(spl[p].ls)p=spl[p].ls;// 找后继
splaying(p,spl[root].rs);//扔到根节点的右儿子的位置
spl[spl[root].rs].ls=spl[root].ls;//顺理成章的让当前根节点的左儿子变成当前节点的右儿子的左儿子
root=spl[root].rs;//把根节点的指针指向当前节点的右儿子
update(root);//更新子树大小
}
else{
root=spl[p].ls;//如果 var 没有后继,直接让它的左儿子当根就好了
}
return;
}
else if(var<spl[p].var){//还是找到要删除的点的位置
del(spl[p].ls,var);
}
else{
del(spl[p].rs,var);
}
return;
}
查询排名,找前驱后继
不想再写了,应该很简单吧。
不过要注意不管哪一种操作都要先把要操作的点扔到根节点发位置去来让树尽可能平衡。
2. 代码时间
标准码风 - 伸展树
无注释版
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e5+5;
struct splay{
int ls;
int rs;
int var;
int sizet;
int cnt;
int lzt;
}spl[N];
int idx,root;
void newnode(int &p,int &var){
p=++idx;
spl[p].var=var;
spl[p].sizet=1;
spl[p].cnt=1;
}
void update(int p){
spl[p].sizet=spl[spl[p].ls].sizet+spl[spl[p].rs].sizet+spl[p].cnt;
}
void zig(int &now){
int l=spl[now].ls;
spl[now].ls=spl[l].rs;
spl[l].rs=now;
now=l;
update(spl[now].rs);
update(now);
}
void zag(int &now){
int r=spl[now].rs;
spl[now].rs=spl[r].ls;
spl[r].ls=now;
now=r;
update(spl[now].ls);
update(now);
}
void splaying(int x,int &y){
if(x==y){
return;
}
int &l=spl[y].ls,&r=spl[y].rs;
if(x==l){
zig(y);
}
else if(x==r){
zag(y);
}
else{
if(spl[x].var<spl[y].var){
if(spl[x].var<spl[l].var){
splaying(x,spl[l].ls);
zig(y);
zig(y);
}
else{
splaying(x,spl[l].rs);
zag(l);
zig(y);
}
}
else{
if(spl[x].var>spl[r].var){
splaying(x,spl[r].rs);
zag(y);
zag(y);
}
else{
splaying(x,spl[r].ls);
zig(r);
zag(y);
}
}
}
}
void add(int &p,int &var){
if(!p){
newnode(p,var);
splaying(p,root);
return ;
}
if(var<spl[p].var){
add(spl[p].ls,var);
}
else if(var>spl[p].var){
add(spl[p].rs,var);
}
else{
spl[p].sizet++;
spl[p].cnt++;
splaying(p,root);
}
}
void del(int p,int var){
if(spl[p].var==var){
splaying(p,root);
if(spl[p].cnt>1){
spl[p].cnt--;
spl[p].sizet--;
return;
}
if(spl[p].rs!=0){
p=spl[p].rs;
while(spl[p].ls)p=spl[p].ls;
splaying(p,spl[root].rs);
spl[spl[root].rs].ls=spl[root].ls;
root=spl[root].rs;
update(root);
}
else{
root=spl[p].ls;
}
return;
}
else if(var<spl[p].var){
del(spl[p].ls,var);
}
else{
del(spl[p].rs,var);
}
return;
}
int ask_rank(int p,int var){
int res=0;
while(p){
if(spl[p].var==var){
res+=spl[spl[p].ls].sizet;
splaying(p,root);
break;
}
else if(var<spl[p].var){
p=spl[p].ls;
}
else {
res+=spl[spl[p].ls].sizet+spl[p].cnt;
p=spl[p].rs;
}
}
return res;
}
int ask_element(int p,int var){
while(p){
if(var-spl[spl[p].ls].sizet>0&&var-(spl[spl[p].ls].sizet+spl[p].cnt)<=0){
splaying(p,root);
return spl[p].var;
}
else if(var-spl[spl[p].ls].sizet<=0){
p=spl[p].ls;
}
else{
var-=spl[spl[p].ls].sizet+spl[p].cnt;
p=spl[p].rs;
}
}
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
int op;
cin>>op;
if(op==1){
int var;
cin>>var;
add(root,var);
}
else if(op==2){
int var;
cin>>var;
del(root,var);
}
else if(op==3){
int var;
cin>>var;
cout<<ask_rank(root,var)+1<<'\n';
}
else if(op==4){
int var;
cin>>var;
cout<<ask_element(root,var)<<'\n';
}
else if(op==5){
int var;
cin>>var;
cout<<ask_element(root,ask_rank(root,var))<<'\n';
}
else if(op==6){
int var;
cin>>var;
cout<<ask_element(root,ask_rank(root,var+1)+1)<<'\n';
}
}
return 0;
}
全注释存档
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e5+5;
struct splay{
int ls;
int rs;
int var;
int sizet;
int cnt;
int lzt;
}spl[N];
int idx,root;
void newnode(int &p,int &var){
p=++idx;
spl[p].var=var;
spl[p].sizet=1;
spl[p].cnt=1;
}
void update(int p){
spl[p].sizet=spl[spl[p].ls].sizet+spl[spl[p].rs].sizet+spl[p].cnt;
}
void zig(int &now){//右旋
int l=spl[now].ls;//拎左
spl[now].ls=spl[l].rs;//右挂左
spl[l].rs=now;//自己变成左边的右儿子
now=l;//更新根的值
update(spl[now].rs);//更新子树大小
update(now);
}
void zag(int &now){//左旋
int r=spl[now].rs;//拎右
spl[now].rs=spl[r].ls;//左挂右
spl[r].ls=now;//自己变成右边的左儿子
now=r;//更新根的值
update(spl[now].ls);//更新子树大小
update(now);
}
void splaying(int x,int &y){
if(x==y){//开始前的特判,相等了直接返回
return;
}
int &l=spl[y].ls,&r=spl[y].rs;//把左右节点能成一个字母的变量方便操作,当然也要用引用传参
if(x==l){//就是目标节点的左儿子,直接做一次右旋就可以了。
zig(y);
}
else if(x==r){//是右儿子,直接做一次左旋就可以了。
zag(y);
}
else{//两种都不符合那么一定是双旋操作了
if(spl[x].var<spl[y].var){//如果当前节点在目标节点的左子树位置
if(spl[x].var<spl[l].var){//如果在目标节点左儿子的左子树位置
splaying(x,spl[l].ls);//只需要把 x 旋转到目标节点左儿子的左儿子的位置
zig(y);//做两次右旋就可以了
zig(y);
}
else{//如果不符合上面的就一定是在目标节点左儿子的右子树位置
splaying(x,spl[l].rs);//只需要把 x 旋转到目标节点左儿子的右儿子的位置
zag(l);//做 zag-zig 就可以了
zig(y);
}
}
else{
if(spl[x].var>spl[r].var){//如果当前节点在目标节点的右子树位置
splaying(x,spl[r].rs);//只需要把 x 旋转到目标节点右儿子的右儿子的位置
zag(y);//做两次左旋就可以了
zag(y);
}
else{//如果不符合上面的就一定是在目标节点右儿子的左子树位置
splaying(x,spl[r].ls);//只需要把 x 旋转到目标节点右儿子的左儿子的位置
zig(r);//做 zig-zag 就可以了
zag(y);
}
}
}
}
void add(int &p,int &var){
if(!p){//没出现过
newnode(p,var);//新建一个
splaying(p,root);//转到根去
return ;
}
if(var<spl[p].var){//往左找
add(spl[p].ls,var);
}
else if(var>spl[p].var){//往右找
add(spl[p].rs,var);
}
else{//出现过了
spl[p].sizet++;//更新树的大小和出现次数
spl[p].cnt++;
splaying(p,root);//扔到根去
}
}
void del(int p,int var){
if(spl[p].var==var){//找到了
splaying(p,root);//二话不说先转到根节点
if(spl[p].cnt>1){//出现次数大于1 很好办了
spl[p].cnt--;
spl[p].sizet--;
return;
}
if(spl[p].rs!=0){//要删除这个点,且这个点有后继
p=spl[p].rs;
while(spl[p].ls)p=spl[p].ls;// 找后继
splaying(p,spl[root].rs);//扔到根节点的右儿子的位置
spl[spl[root].rs].ls=spl[root].ls;//顺理成章的让当前根节点的左儿子变成当前节点的右儿子的左儿子
root=spl[root].rs;//把根节点的指针指向当前节点的右儿子
update(root);//更新子树大小
}
else{
root=spl[p].ls;//如果 var 没有后继,直接让它的左儿子当根就好了
}
return;
}
else if(var<spl[p].var){//还是找到要删除的点的位置
del(spl[p].ls,var);
}
else{
del(spl[p].rs,var);
}
return;
}
int ask_rank(int p,int var){
int res=0;
while(p){
if(spl[p].var==var){
res+=spl[spl[p].ls].sizet;
splaying(p,root);
break;
}
else if(var<spl[p].var){
p=spl[p].ls;
}
else {
res+=spl[spl[p].ls].sizet+spl[p].cnt;
p=spl[p].rs;
}
}
return res;
}
int ask_element(int p,int var){
while(p){
if(var-spl[spl[p].ls].sizet>0&&var-(spl[spl[p].ls].sizet+spl[p].cnt)<=0){
splaying(p,root);
return spl[p].var;
}
else if(var-spl[spl[p].ls].sizet<=0){
p=spl[p].ls;
}
else{
var-=spl[spl[p].ls].sizet+spl[p].cnt;
p=spl[p].rs;
}
}
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
int op;
cin>>op;
if(op==1){
int var;
cin>>var;
add(root,var);
}
else if(op==2){
int var;
cin>>var;
del(root,var);
}
else if(op==3){
int var;
cin>>var;
cout<<ask_rank(root,var)+1<<'\n';
}
else if(op==4){
int var;
cin>>var;
cout<<ask_element(root,var)<<'\n';
}
else if(op==5){
int var;
cin>>var;
cout<<ask_element(root,ask_rank(root,var))<<'\n';
}
else if(op==6){
int var;
cin>>var;
cout<<ask_element(root,ask_rank(root,var+1)+1)<<'\n';
}
}
return 0;
}
3. 用 Splay 维护区间操作
az,评价是不如 Fhq Treap 好写且功能全面。
(逃
迁移自洛谷


 浙公网安备 33010602011771号
浙公网安备 33010602011771号