Fhq Treap
前言
神仙数据结构!!!!
由 范浩强(Fan hao qiang) 神犇发明的数据结构,Orz。
别称无旋 Treap,没有了普通 Treap 复杂的旋转操作,但依然可以轻松的维护区间和可持久化。
1. 原理
Fhq Treap 不同于普通的 Treap 使用旋转维护堆特性,而是直接在 Treap 中按照某些标准分裂出两块新 Treap,在两个新 Treap 中间插入目标节点,再把三者合并来来维护堆的特性,因此 Fhq Treap 有两个关键操作:分裂 (split)与合并 (merge)。
在分裂的过程中,Fhq Treap 会在节点的值位置处分裂,在分裂处插入新值来维护二叉搜索树的性质。
在合并的过程中,Fhq Treap 会根据赋予节点的一个随机值来维护堆的特性。
Fhq Treap 也是一种动态开点树,因此维护值域时无需离散化。
还是用万年不变的例题P3369 【模板】普通平衡树
首先来说说 struct 里怎么写:
struct ftp{
int ls;
int rs;
int var;
unsigned int hvar;
int sizet;
}fhq[N];
int cnt=0,root;
mt19937 rnd(114514);
int ls int rs 代表 Fhq Treap 上这个节点存储的左儿子和右儿子;int var 代表这个节点的值;unsigned int hvar 是一个用来维护 Fhq Treap 堆特性的随机值,由下方的随机数生成器 mt19937 rnd(<seed>) 生成,什么是 mt19937?
最后一个 int sizet 表示这个节点领导的子树的大小。
全局变量 int cnt 记录开点的编号,int root 记录当前Fhq Treap 的根节点。
创建一个新的点 & 更新子树大小
没什么好说的,注意给新点赋上一个随机的权值
int newnode(int var){
fhq[++cnt].ls=0;
fhq[cnt].rs=0;
fhq[cnt].var=var;
fhq[cnt].hvar=rnd();
fhq[cnt].sizet=1;
return cnt;
}
void update(int p){
fhq[p].sizet=fhq[fhq[p].ls].sizet+fhq[fhq[p].rs].sizet+1//自己也算一个点,要加上自己;
}
分裂操作
对于只维护全局的 Fhq Treap,分裂的标准一般是节点的权值。
我们采用递归的方式分裂 Fhq Treap,首先定义我们分裂后的两个 Fhq Treap 树根的编号为 \(x,y\)。
考虑下面的情况,我们对这样一个 Fhq Treap 以大于等于 \(13\) 为标准进行分裂:
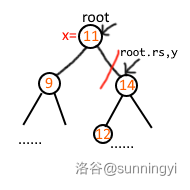
一开始的根节点在 \(11\) 的位置,此时由于其小于我们定义的标准,将分裂的左子树根给予 \(11\)(即操作 \(x=11\)),之后向右尝试分裂 \(11\) 的右子树。
为什么还要向右尝试呢,因为二叉搜索树的特性,右子树的左子树可能还会出现比标准小的情况。
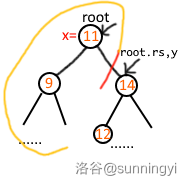
这时,由于当前的根的权值大于我们的标准,将分裂的右子树根给予 \(14\),接着尝试向左分裂当前根的左子树。
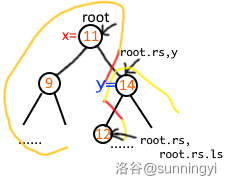
此时由于当前节点小于标准,将当前节点作为左子树根的右儿子:
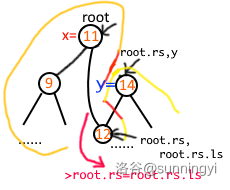
这时有点问题:\(12\) 节点既是分裂左子树的右儿子,又是分裂右子树的左儿子,如何避免这种问题?
我们可以大胆往下找,由于我们并没有给叶子节点赋左儿子右儿子,因此这样会让我们走到初始值 \(0\) 的位置。
如果当前走到了不存在的节点,也就是编号等于初始值 \(0\),如果这个点是其父亲节点的右子树,我们就让左子树根的右儿子给到这个点;如果这个点是其父亲节点的左子树,我们就让右子树根的左儿子给到这个点。
可以看图理解一下:
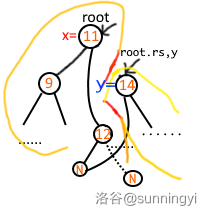
显然,在一个不存在的点上出现左右儿子重合的情况并不影响我们之后的求解。
上面说的情况都是只向下一层的情况,多层的情况看起来很复杂,但其实在函数中用引用传参就可以很简单的解决:
void split(int p,int var,int &x,int &y){
if(!p){//不存在的点
x=y=0;//左右儿子都指向这个不存在的点
//因为 x,y 的其中一个一定是当前节点的父节点,所以直接平等对待就可以了,至于为什么可以看看下面
return;
}
if(fhq[p].var<=var){
//此时根节点和左边一定归属在左半部分,于是赋值并向右寻找
x=p;
split(fhq[p].rs,var,fhq[p].rs,y);
//根节点更新为当前的右子节点,同时因为可能出现右子树的左子树比标准小的情况
//因此还要尝试更新当前的右子节点以将右边可能的部分与左边联系起来
}
else{//归属到右半部分的情况和左边一样,不重复写了。
y=p;
split(fhq[p].ls,var,x,fhq[p].ls);
}
update(p);//更新p的树的大小
return;
}
合并操作
合并时,Fhq Treap 将两个树按照给予的那个随机值(以下简称堆值)进行合并以维护堆的特性,我们以大根堆为例。
考虑下面的合并情况,合并的两颗子树的根分别是 \(x,y\):
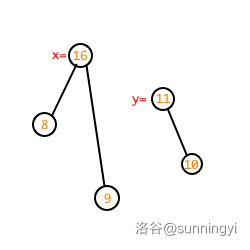
首先比较当前两个节点堆值的大小,大的一方当父亲,小的一方当儿子,至于是左儿子还是右儿子需要看具体的占位情况。
在我们的例子中,\(y\) 所指的节点要当 \(x\) 的右儿子,因此此时我们仅需要考虑 \(x\) 的右儿子和 \(y\) 合并的结果(把 \(x\) 当前的右儿子合并走才能让 \(y\) 当右儿子):
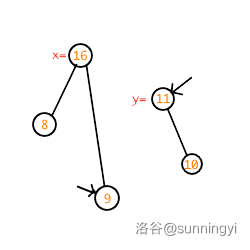
重复比较过程,很明显此时要让 \(y\) 当父亲,那么考虑 \(y\) 的左儿子与 \(x\) 的右儿子合并:
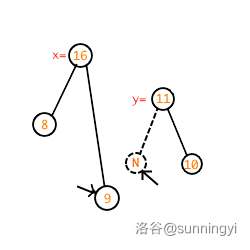
此时你会发现,\(y\) 的右儿子不存在(是初始值),这也就是说 \(x\) 的右儿子可以直接合并过来了:
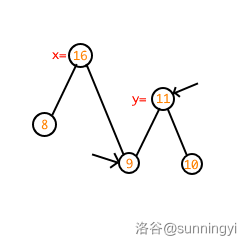
\(x\) 的右儿子既然已经空闲,可以让 \(y\) 合并到 \(x\) 的右儿子了,这一过程在递归回来时实现:
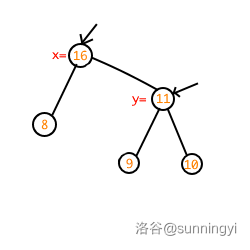
于是我们成功的完成了合并操作!
int merge(int x,int y){
if(!x||!y)return x+y;//没有了直接返回有值的那个
if(fhq[x].hvar>fhq[y].hvar){//x当爸爸,y当儿子
fhq[x].rs=merge(fhq[x].rs,y);//递归赋值
update(x);//更新 x 的大小
return x;//返回完成合并的编号来进行下一次合并
}
else{//反过来
fhq[y].ls=merge(x,fhq[y].ls);
update(y);
return y;
}
}
插入点操作
设我们要插入的值为 \(var\)。
利用上文的 split 和 merge 操作,将整个 Fhq Treap 按照 \(var\) 的值裂开,同时用 \(var\) 值创建一个新的点,按照 左边、新点、右边 的顺序合并起来就好了。
这真的比 Treap 简单多了
void add(int var){
split(root,var,x,y);
root=merge(merge(x,newnode(var)),y);
//合并时可能会更新根节点因此要赋值
return;
}
删除点操作
设我们要删除的点的值为 \(var\)。
还是利用 split 和 merge,首先用 split 把整棵树按照 \(var\) 裂成两块,再把左边那一块按照 \(var-1\) 裂成两块。很明显中间那一块的值一定全都是 \(var\),因为只删一个,就把中间子树根节点删去,也就是合并中间根节点的左右儿子,再把这三块从左到右合并就可以了。
这真的比 Treap 简单多了*2
void del(int var){
split(root,var,x,z);//裂成两块
split(x,var-1,x,y);//左边的也裂成两块
y=merge(fhq[y].ls,fhq[y].rs);//只合并左右,不要根节点
root=merge(merge(x,y),z);//从左到右合并,注意更新 root
}
查询某个值的排名
设这个值为 \(var\)。
还是用 split 将整棵树按照 \(var-1\) 裂成两块,则题目中的排名等价于左子树大小加一。
当然算完了别忘了合并回去。
怎么不说了
int ask_rank(int var){
split(root,var-1,x,y);
int res=fhq[x].sizet+1;
root=merge(x,y);
return res;
}
查询某个排名对应的值
这个就和普通的平衡树甚至是线段树没有区别了,这里提供两种写法:
int ask_element(int var){//非递归
int p=root;
while(p){
if(fhq[fhq[p].ls].sizet+1==var){
break;
}
else if(fhq[fhq[p].ls].sizet>=var){
p=fhq[p].ls;
}
else{
var-=fhq[fhq[p].ls].sizet+1;//这里一定要多减一个,递归版同样
p=fhq[p].rs;
}
}
return fhq[p].var;
}
int ask_element(int p,int var){//递归
if(fhq[fhq[p].ls].sizet+1==var){
return fhq[p].var;
}
else if(fhq[fhq[p].ls].sizet>=var){
return ask_element(fhq[p].ls,var);
}
else{
return ask_element(fhq[p].rs,var-fhq[fhq[p].ls].sizet-1);
}
}
查询前驱
设要查询前驱的值为 \(var\)。
用 split 操作把整棵树按照 \(var-1\) 裂成两半,那么根据二叉查找树的特性,只需要在左边的子树里尽量往右找就可以了。
别忘了合回去。
int ask_pre(int var){
split(root,var-1,x,y);
int p=x;
while(fhq[p].rs){
p=fhq[p].rs;
}
root=merge(x,y);
return fhq[p].var;
}
查询后继
设要查询前驱的值为 \(var\)。
用 split 操作把整棵树按照 \(var\) 裂成两半,那么根据二叉查找树的特性,只需要在右边的子树里尽量往左找就可以了。别忘了合回去。
int ask_suc(int var){
split(root,var,x,y);
int p=y;
while(fhq[p].ls){
p=fhq[p].ls;
}
root=merge(x,y);
return fhq[p].var;
}
2. 代码时间
标准码风 - Fhq Treap
无注释版
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e5+5;
struct ftp{
int ls;
int rs;
int var;
unsigned int hvar;
int sizet;
}fhq[N];
int cnt=0,root;
mt19937 rnd(114514);
int x,y,z;
int newnode(int var){
fhq[++cnt].ls=0;
fhq[cnt].rs=0;
fhq[cnt].var=var;
fhq[cnt].hvar=rnd();
fhq[cnt].sizet=1;
return cnt;
}
void update(int p){
fhq[p].sizet=fhq[fhq[p].ls].sizet+fhq[fhq[p].rs].sizet+1;
}
void split(int p,int var,int &x,int &y){
if(!p){
x=y=0;
return;
}
if(fhq[p].var<=var){
x=p;
split(fhq[p].rs,var,fhq[p].rs,y);
}
else{
y=p;
split(fhq[p].ls,var,x,fhq[p].ls);
}
update(p);
return;
}
int merge(int x,int y){
if(!x||!y)return x+y;
if(fhq[x].hvar<fhq[y].hvar){
fhq[x].rs=merge(fhq[x].rs,y);
update(x);
return x;
}
else{
fhq[y].ls=merge(x,fhq[y].ls);
update(y);
return y;
}
}
void add(int var){
split(root,var,x,y);
root=merge(merge(x,newnode(var)),y);
return;
}
void del(int var){
split(root,var,x,z);
split(x,var-1,x,y);
y=merge(fhq[y].ls,fhq[y].rs);
root=merge(merge(x,y),z);
}
int ask_rank(int var){
split(root,var-1,x,y);
int res=fhq[x].sizet+1;
root=merge(x,y);
return res;
}
int ask_element(int var){
int p=root;
while(p){
if(fhq[fhq[p].ls].sizet+1==var){
break;
}
else if(fhq[fhq[p].ls].sizet>=var){
p=fhq[p].ls;
}
else{
var-=fhq[fhq[p].ls].sizet+1;
p=fhq[p].rs;
}
}
return fhq[p].var;
}
int ask_element(int p,int var){
if(fhq[fhq[p].ls].sizet+1==var){
return fhq[p].var;
}
else if(fhq[fhq[p].ls].sizet>=var){
return ask_element(fhq[p].ls,var);
}
else{
return ask_element(fhq[p].rs,var-fhq[fhq[p].ls].sizet-1);
}
}
int ask_pre(int var){
split(root,var-1,x,y);
int p=x;
while(fhq[p].rs){
p=fhq[p].rs;
}
root=merge(x,y);
return fhq[p].var;
}
int ask_suc(int var){
split(root,var,x,y);
int p=y;
while(fhq[p].ls){
p=fhq[p].ls;
}
root=merge(x,y);
return fhq[p].var;
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
int op,var;
op=rd;
var=rd;
if(op==1){
add(var);
}
else if(op==2){
del(var);
}
else if(op==3){
cout<<ask_rank(var)<<'\n';
}
else if(op==4){
cout<<ask_element(root,var)<<'\n';
}
else if(op==5){
cout<<ask_pre(var)<<'\n';
}
else if(op==6){
cout<<ask_suc(var)<<'\n';
}
}
return 0;
}
全注释存档
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e5+5;
struct ftp{
int ls;
int rs;
int var;
unsigned int hvar;
int sizet;
}fhq[N];
int cnt=0,root;
mt19937 rnd(114514);
int x,y,z;
int newnode(int var){
fhq[++cnt].ls=0;
fhq[cnt].rs=0;
fhq[cnt].var=var;
fhq[cnt].hvar=rnd();
fhq[cnt].sizet=1;
return cnt;
}
void update(int p){
fhq[p].sizet=fhq[fhq[p].ls].sizet+fhq[fhq[p].rs].sizet+1//自己也算一个点,要加上自己;
}
void split(int p,int var,int &x,int &y){
if(!p){//不存在的点
x=y=0;//左右儿子都指向这个不存在的点
//因为 x,y 的其中一个一定是当前节点的父节点,所以直接平等对待就可以了,至于为什么可以看看下面
return;
}
if(fhq[p].var<=var){
//此时根节点和左边一定归属在左半部分,于是赋值并向右寻找
x=p;
split(fhq[p].rs,var,fhq[p].rs,y);
//根节点更新为当前的右子节点,同时因为可能出现右子树的左子树比标准小的情况
//因此还要尝试更新当前的右子节点以将右边可能的部分与左边联系起来
}
else{//归属到右半部分的情况和左边一样,不重复写了。
y=p;
split(fhq[p].ls,var,x,fhq[p].ls);
}
update(p);//更新p的树的大小
return;
}
int merge(int x,int y){
if(!x||!y)return x+y;//没有了直接返回有值的那个
if(fhq[x].hvar>fhq[y].hvar){//x当爸爸,y当儿子
fhq[x].rs=merge(fhq[x].rs,y);//递归赋值
update(x);//更新 x 的大小
return x;//返回完成合并的编号来进行下一次合并
}
else{//反过来
fhq[y].ls=merge(x,fhq[y].ls);
update(y);
return y;
}
}
void add(int var){
split(root,var,x,y);
root=merge(merge(x,newnode(var)),y);
//合并时可能会更新根节点因此要赋值
return;
}
void del(int var){
split(root,var,x,z);//裂成两块
split(x,var-1,x,y);//左边的也裂成两块
y=merge(fhq[y].ls,fhq[y].rs);//只合并左右,不要根节点
root=merge(merge(x,y),z);//从左到右合并,注意更新 root
}
int ask_rank(int var){
split(root,var-1,x,y);
int res=fhq[x].sizet+1;
root=merge(x,y);
return res;
}
int ask_element(int var){//非递归
int p=root;
while(p){
if(fhq[fhq[p].ls].sizet+1==var){
break;
}
else if(fhq[fhq[p].ls].sizet>=var){
p=fhq[p].ls;
}
else{
var-=fhq[fhq[p].ls].sizet+1;//这里一定要多减一个
p=fhq[p].rs;
}
}
return fhq[p].var;
}
int ask_element(int p,int var){//递归
if(fhq[fhq[p].ls].sizet+1==var){
return fhq[p].var;
}
else if(fhq[fhq[p].ls].sizet>=var){
return ask_element(fhq[p].ls,var);
}
else{
return ask_element(fhq[p].rs,var-fhq[fhq[p].ls].sizet-1);
}
}
int ask_pre(int var){
split(root,var-1,x,y);
int p=x;
while(fhq[p].rs){
p=fhq[p].rs;
}
root=merge(x,y);
return fhq[p].var;
}
int ask_suc(int var){
split(root,var,x,y);
int p=y;
while(fhq[p].ls){
p=fhq[p].ls;
}
root=merge(x,y);
return fhq[p].var;
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
int op,var;
op=rd;
var=rd;
if(op==1){
add(var);
}
else if(op==2){
del(var);
}
else if(op==3){
cout<<ask_rank(var)<<'\n';
}
else if(op==4){
cout<<ask_element(root,var)<<'\n';
}
else if(op==5){
cout<<ask_pre(var)<<'\n';
}
else if(op==6){
cout<<ask_suc(var)<<'\n';
}
}
return 0;
}
3. Fhq Treap 维护区间操作
还是来看一道经典题 P3391 【模板】文艺平衡树。
这个板子题看似只让你维护一种操作,但其实它表明了 Fhq Treap 可以当更高级的线段树用的性质。
首先这种 Fhq Treap 分裂的标准不再是值的大小了,而是树的大小。
那么这样就会有一个很好的性质,
假设我们要对区间 \(l,r\) 做操作,
先按照 \(l-1\) 把 Fhq Treap 分成两部分,在按照 \(r-l+1\) 把右边那个子树分成两部分
很显然中间的那个子树代表的就是区间 \(l,r\)。
然后就可以进行任何操作了~
当然 Fhq Treap 也有懒标记这个东西。
在找到这个区间的时候可以先把懒标记打上,需要的时候就下传。
而且 Fhq Treap 还可以实现一些线段树无法实现的东西,比如说这个区间翻转。
区间翻转是怎么实现的呢?交换左右儿子!
就是这么暴力
但是也要把懒标记下穿到子树里不能只在上面翻转。
输出答案的话其实就是整个 Fhq Treap 的中序遍历。
当然由于 Fhq Treap 动态开点的特性,甚至可以完成在数组中间插入,删除某个数结合区间翻转的操作,区间加之类的操作就更不用说了。
下面就是数组中间插入,删除某个数结合区间翻转的模板代码,小小的 Fhq Treap。
震撼
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e5+5;
struct ftp{
int ls;
int rs;
int var;
unsigned int hvar;
int sizet;
bool lzt;
}fhq[N];
int cnt=0,root;
mt19937 rnd(114514);
int x,y,z;
int newnode(int var){
fhq[++cnt].ls=0;
fhq[cnt].rs=0;
fhq[cnt].var=var;
fhq[cnt].hvar=rnd();
fhq[cnt].sizet=1;
return cnt;
}
void update(int p){
fhq[p].sizet=fhq[fhq[p].ls].sizet+fhq[fhq[p].rs].sizet+1;
}
void pushdown(int p){
if(fhq[p].lzt==0)return;
swap(fhq[p].ls,fhq[p].rs);
fhq[fhq[p].ls].lzt^=1;
fhq[fhq[p].rs].lzt^=1;
fhq[p].lzt=0;
}
void split(int p,int siz,int &x,int &y){
if(!p){
x=y=0;
return;
}
pushdown(p);
if(fhq[fhq[p].ls].sizet<siz){
x=p;
split(fhq[p].rs,siz-fhq[fhq[p].ls].sizet-1,fhq[p].rs,y);
}
else{
y=p;
split(fhq[p].ls,siz,x,fhq[p].ls);
}
update(p);
return;
}
int merge(int x,int y){
if(!x||!y)return x+y;
if(fhq[x].hvar<fhq[y].hvar){
pushdown(x);
fhq[x].rs=merge(fhq[x].rs,y);
update(x);
return x;
}
else{
pushdown(y);
fhq[y].ls=merge(x,fhq[y].ls);
update(y);
return y;
}
}
void add(int l,int var){
split(root,l-1,x,y);
root=merge(merge(x,newnode(var)),y);
return;
}
void del(int l){
split(root,l,y,z);
split(y,l-1,x,y);
root=merge(x,z);
}
void rev(int l,int r){
split(root,l-1,x,y);
split(y,r-l+1,y,z);
fhq[y].lzt^=1;
root=merge(merge(x,y),z);
return;
}
void print(int p){
if(!p)return;
pushdown(p);
print(fhq[p].ls);
cout<<fhq[p].var<<' ';
print(fhq[p].rs);
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
root=merge(root,newnode(i));
}
for(int i=1;i<=m;i++){
string op;
cin>>op;
if(op=="apos"){
int x,z;
cin>>x>>z;
add(x,z);
}
else if(op=="dpos"){
int x;
cin>>x;
del(x);
}
else if(op=="rev"){
int l,r;
cin>>l>>r;
rev(l,r);
}
else if(op=="p"){
print(root);
cout<<'\n';
}
else{
cout<<"undef command re-enter>"<<'\n';
}
}
return 0;
}
bye~
迁移自洛谷


 浙公网安备 33010602011771号
浙公网安备 33010602011771号