珂朵莉树
前言 & 鲜花
暴力美学,骗分神器
珂朵莉树来自这道题。
这篇文章将其作为模板题。
1. 原理
珂朵莉树本质还是暴力,但是它将每个数值相同的区间使用一个块独立保存,优化了一些时间。
很显然,如果保证样例在处理过程中没有两个相邻的数字是一样的,珂朵莉树就和暴力没区别了,甚至还有比暴力更高的复杂度。
由于上面的限制,珂朵莉树适合处理有 “区间推平” 操作的题目,比如我们的模板题中提到的操作 \(2\):
\(2\) \(l\) \(r\) \(x\) :将\([l,r]\) 区间所有数改成\(x\)。
大致来说,珂朵莉树使用 set 维护相同值组成的块组成的序列,对于每一次操作,首先使用 set 查找可能的左右区间并对这两个区间进行分离(split),之后对属于区间内部的块进行操作。
因为是数据结构,先来说说 struct 怎么写:
珂朵莉树维护相同值的块,因此其中存储着区间左端点 int l,区间右端点 int r,区间值 mutable long long v:
struct cht{
ll l,r;
mutable ll v;
cht(ll l,ll r=-1,ll v=1){
this->l=l;
this->r=r;
this->v=v;
}
bool operator<(const cht &x)const{
return l<x.l;
}
};
set<cht> chttree;
typedef set<cht>::iterator iter;
其中定义了一个构造函数用于 split() 操作,重载了一个运算符使每一个块在 set 中可以按照区间左端点排序。
什么是 mutable 呢?因为我们要对区间进行操作,势必要改变某些块中 v 的值,但是 set 的迭代器是只读的,这个关键字可以让值在只读的方法中也可以被修改。
要注意,这里重载的顺序和优先队列 priority_queue 不同。
由于珂朵莉树多次使用迭代器,因此我们把它 typedef 掉。
分裂操作 split
因为珂朵莉树中只是维护相同值的块,因此当我们想区间修改或查询时可能遇到区间左右端点在块的中间的情况,这时需要使用 split 分裂区间以正确的对区间进行更新。
iter split(int pos) 函数返回以 \(pos\) 为区间左端点的迭代器。
首先当然要先看看当前树中有没有这样以 \(pos\) 为区间左端点的块,这时候可以使用 set 自带的 lower_bound 函数。(使用 algorithm 库中的 lower_bound 和 upper_bound 函数对 set 中的元素进行查询,时间复杂度为 \(O(n)\)。)
iter it=chttree.lower_bound(cht(pos));
if(it!=chttree.end()&&it->l==pos){
return it;
}
注意一定要把 it!=chttree.end() 这个判断放在前面,防止 RE。
如果没有想要的,我们就要分裂区间了。
由于 lower_bound 查找的是 “大于等于”,而我们又没有发现等于,这意味这此时的迭代器区间指向的块的左端点大于 \(pos\),那么 \(pos\) 一定在前一个块的范围内,于是我们把迭代器退回去一个。
但是,退回去后如果这个块的右端点却又小于 \(pos\),证明我们根本没有这个区间,此时返回 set 的末尾迭代器。
it--;
if(it->r<pos)return chttree.end();
此时我们先删除这个迭代器代表的块,把这个块分裂成 \([l,pos-1]\) 和 \([pos,r]\) 两块,再放回 set 中,并返回块 \([pos,r]\) 的迭代器。
ll L=it->l;//把要删除的块的信息先保存下来
ll R=it->r;
ll V=it->v;
chttree.erase(it);
chttree.insert(cht{L,pos-1,V});
return chttree.insert(cht{pos,R,V}).first;
/*
insert().first 返回插入块的迭代器
insert().second 返回是否插入成功(是否先前已有相同的元素)
*/
区间推平操作 assign
void assign(ll l,ll r,ll k) 函数将区间 \(l,r\) 范围内的所有数设置为 \(k\)。
首先我们调用两次 split 函数将我们想要的块分裂开来,之后删掉这两个块之间的所有块,重新插入一个新的块代表区间 \(l,r\) 的值均为 \(k\)。
void assign(ll l,ll r,ll k){
iter itr=split(r+1),itl=split(l);
//这里切 r+1 而不是 r 的原因是 set.erase(beg,end) 遵循左闭右开原则
chttree.erase(itl,itr);
chttree.insert(cht{l,r,k});
return;
}
为什么要先 split(r+1) 再 split(l)?这里引用原题洛谷题解里@泥土笨笨 老师的解释:
现在说一下为啥大部分题解都不对,注意刚刚
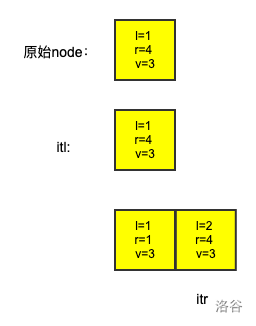
assign函数里面调用的那两次split,我是先split(r+1),计算出itr,然后再split(l),计算itl的。这个顺序不能反。为啥不能反?举个具体例子,比如现在有个区间是 \([1,4]\),我们想从里面截取 \([1,1]\) 出来,那么我们需要调用两次
split,分别是split(2)和split(1)。假设先调用
split(1),如图中间的结果:现在的
itl指向的还是原来的那个node,没有什么变化。但是当我们后续调用itr的时候,出事儿了。因为这时候,我们把原来的 \([1,4]\) 区间删掉了,拆成了两份,itr指向的是后面那个,但是原来itl指向的那个已经被erase掉了。这时候用itl和itr调用s.erase的时候就会出问题,直接 RE。有同学说我顺序反了没 RE 啊,也 AC。恭喜你,你人品好。这东西理论上会 RE,但是实际上概率不大,我对拍了一下,大概 \(1\%\) 的概率 RE 吧。但是人品不好的同学,可能上来就 RE 一片,而且是随机 RE,同一个数据,一会儿能过,一会儿过不了。所以,还是别给自己找麻烦了。
区间加操作 add
void add(ll l,ll r,ll k) 函数将区间 \(l,r\) 范围内的所有数加 \(k\)。
还是先把块拆开,之后用迭代器给每一个块的值加 \(k\) 就可以了。
void add(ll l,ll r,ll k){
iter itr=split(r+1),itl=split(l);
iter iit=itl;
//左闭右开原则也便利了迭代器范围的判断
for(;iit!=itr;iit++){
iit->v+=k;
}
return;
}
这真的太暴力了
其他操作不列举了,这里给个伪代码模板:
operators(left,right, ...){
iter itr=split(r+1),itl=split(l);
iter iit=itl;
for(;iit!=itr;iit++){
operators
}
return any;
}
2. 实现
以下代码可通过 CF896C。
标准码风 - 珂朵莉树
无注释版
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int mod=1e9+7;
ll ret;
ll seed;
ll n,m;
ll vmax;
ll rnd(){
ret=seed;
seed=(seed*7+13)%mod;
return ret;
}
ll a[100005];
struct cht{
ll l,r;
mutable ll v;
cht(ll l,ll r=-1,ll v=1){
this->l=l;
this->r=r;
this->v=v;
}
bool operator<(const cht &x)const{
return l<x.l;
}
};
struct sortab{
int sizet;
ll v;
}st[100005];
int cnt=0;
set<cht> chttree;
typedef set<cht>::iterator iter;
bool cmp(sortab x,sortab y){
return x.v<y.v;
}
iter split(int pos){
iter it=chttree.lower_bound(cht(pos));
if(it!=chttree.end()&&it->l==pos){
return it;
}
it--;
if(it->r<pos)return chttree.end();
ll L=it->l;
ll R=it->r;
ll V=it->v;
chttree.erase(it);
chttree.insert(cht{L,pos-1,V});
return chttree.insert(cht{pos,R,V}).first;
}
void assign(ll l,ll r,ll k){
iter itr=split(r+1),itl=split(l);
chttree.erase(itl,itr);
chttree.insert(cht{l,r,k});
return;
}
void add(ll l,ll r,ll k){
iter itr=split(r+1),itl=split(l);
iter iit=itl;
for(;iit!=itr;iit++){
iit->v+=k;
}
return;
}
ll kelement(ll l,ll r,ll k){
iter itr=split(r+1),itl=split(l);
iter iit=itl;
cnt=0;
for(;iit!=itr;iit++){
++cnt;
st[cnt].sizet=(iit->r-iit->l+1);
st[cnt].v=iit->v;
}
sort(st+1,st+1+cnt,cmp);
ll f=1;
while(k>0){
k-=st[f].sizet;
f++;
}
return st[f-1].v;
}
ll ksm(ll a,ll b,ll y){
ll res=1,t=a;
while(b){
if(b&1==1){
res=(res*t)%y;
}
t=t*t%y;
b=b>>1;
}
return res;
}
ll query(ll l,ll r,ll x,ll y){
iter itr=split(r+1),itl=split(l);
iter iit=itl;
ll res=0;
for(;iit!=itr;iit++){
ll sub=ksm(iit->v%y,x,y);
res=(res+sub*(iit->r-iit->l+1)%y)%y;
}
return res;
}
int main(){
cin>>n>>m>>seed>>vmax;
for(int i=1;i<=n;i++){
a[i]=(rnd()%vmax)+1;
chttree.insert(cht{i,i,a[i]});
}
for(int i=1;i<=m;i++){
ll op=(rnd()%4)+1;
ll l=(rnd()%n)+1;
ll r=(rnd()%n)+1;
if(l>r)swap(l,r);
ll x,y;
if(op==3){
x=(rnd()%(r-l+1))+1;
}
else{
x=(rnd()%vmax)+1;
}
if(op==4){
y=(rnd()%vmax)+1;
}
if(op==1){
add(l,r,x);
}
else if(op==2){
assign(l,r,x);
}
else if(op==3){
cout<<kelement(l,r,x)<<'\n';
}
else if(op==4){
cout<<query(l,r,x,y)<<'\n';
}
}
return 0;
}
全注释存档
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int mod=1e9+7;
ll ret;
ll seed;
ll n,m;
ll vmax;
ll rnd(){
ret=seed;
seed=(seed*7+13)%mod;
return ret;
}
ll a[100005];
struct cht{
ll l,r;
mutable ll v;
cht(ll l,ll r=-1,ll v=1){
this->l=l;
this->r=r;
this->v=v;
}
bool operator<(const cht &x)const{
return l<x.l;
}
};
struct sortab{
int sizet;
ll v;
}st[100005];
int cnt=0;
set<cht> chttree;
typedef set<cht>::iterator iter;
bool cmp(sortab x,sortab y){
return x.v<y.v;
}
iter split(int pos){
iter it=chttree.lower_bound(cht(pos));
if(it!=chttree.end()&&it->l==pos){
return it;
}
it--;
if(it->r<pos)return chttree.end();
ll L=it->l;//把要删除的块的信息先保存下来
ll R=it->r;
ll V=it->v;
chttree.erase(it);
chttree.insert(cht{L,pos-1,V});
return chttree.insert(cht{pos,R,V}).first;
/*
insert().first 返回插入块的迭代器
insert().second 返回是否插入成功(是否先前已有相同的元素)
*/
}
void assign(ll l,ll r,ll k){
iter itr=split(r+1),itl=split(l);
//这里切 r+1 而不是 r 的原因是 set.erase(beg,end) 遵循左闭右开原则
chttree.erase(itl,itr);
chttree.insert(cht{l,r,k});
return;
}
void add(ll l,ll r,ll k){
iter itr=split(r+1),itl=split(l);
iter iit=itl;
//左闭右开原则也便利了迭代器范围的判断
for(;iit!=itr;iit++){
iit->v+=k;
}
return;
}
ll kelement(ll l,ll r,ll k){
iter itr=split(r+1),itl=split(l);
iter iit=itl;
cnt=0;
for(;iit!=itr;iit++){
++cnt;
st[cnt].sizet=(iit->r-iit->l+1);
st[cnt].v=iit->v;
}
sort(st+1,st+1+cnt,cmp);
ll f=1;
while(k>0){
k-=st[f].sizet;
f++;
}
return st[f-1].v;
}
ll ksm(ll a,ll b,ll y){
ll res=1,t=a;
while(b){
if(b&1==1){
res=(res*t)%y;
}
t=t*t%y;
b=b>>1;
}
return res;
}
ll query(ll l,ll r,ll x,ll y){
iter itr=split(r+1),itl=split(l);
iter iit=itl;
ll res=0;
for(;iit!=itr;iit++){
ll sub=ksm(iit->v%y,x,y);
res=(res+sub*(iit->r-iit->l+1)%y)%y;
}
return res;
}
//operators(left,right, ...){
// iter itr=split(r+1),itl=split(l);
// iter iit=itl;
// for(;iit!=itr;iit++){
// opertaors
// }
// return any;
//}
//priority_queue<cht> ct;
int main(){
cin>>n>>m>>seed>>vmax;
for(int i=1;i<=n;i++){
a[i]=(rnd()%vmax)+1;
chttree.insert(cht{i,i,a[i]});
// ct.push(cht{i,i,a[i]});
}
// ?????
// for(iter it=chttree.begin();it!=chttree.end();it++){
// cout<<it->v<<' '<<it->l<<' '<<it->r<<'\n';
// }
// while(ct.size()){
// cht e=ct.top();
// ct.pop();
// cout<<e.v<<' '<<e.l<<' '<<e.r<<'\n';
// }
for(int i=1;i<=m;i++){
ll op=(rnd()%4)+1;
ll l=(rnd()%n)+1;
ll r=(rnd()%n)+1;
if(l>r)swap(l,r);
ll x,y;
if(op==3){
x=(rnd()%(r-l+1))+1;
}
else{
x=(rnd()%vmax)+1;
}
if(op==4){
y=(rnd()%vmax)+1;
}
if(op==1){
add(l,r,x);
}
else if(op==2){
assign(l,r,x);
}
else if(op==3){
cout<<kelement(l,r,x)<<'\n';
}
else if(op==4){
cout<<query(l,r,x,y)<<'\n';
}
}
return 0;
}
3. 鲜花
怎么这么多鲜花
珂朵莉树也是一种动态数据结构,可以处理一些区间范围过大普通线段树开不下的情况。
想用一种不暴力的数据结构解决此问题可以使用动态开点线段树。
例如这道题。
迁移自洛谷


 浙公网安备 33010602011771号
浙公网安备 33010602011771号