概率

前言

高中数学必修二第十章和选择性必修三第七章。

1. 随机事件与概率

将对随机事件的实现和对他的观察称为 随机试验，用大写字母 \(E\) 来表示。
随机实验有三种特性：

• 实验可重复性。
• 结果可预知性（知道有那些结果，且结果数量不为 \(1\) ）
• 结果随机性（结果在实验前不能确定，且每一次实验总是会恰好出现一种结果）。

将随机实验每个可能的结果称为 样本点，将全体样本点组成的集合称为 样本空间。
用 \(\Omega\) 表示样本空间，用 \(\omega\) 表示一个样本点。当然对于很多的样本空间，可以使用 \(\omega_1,\omega_2\cdots\) 来表示。
当一个样本空间内的样本点的个数有限时，这个样本空间被称为 有限样本空间。
因为一个样本空间是一个集合，我们把样本空间这个集合的非空真子集称为 随机事件（简称事件），只包含一个样本点的随机事件称为 基本事件。
例如，对于扔六面体骰子扔出的点数这一随机实验，其样本空间为：

\[\Omega =\{1，2，3，4，5，6 \} \]

对于事件 “扔出的点数为奇数”，对应的子集为：

\[\Omega=\{1,3,5\} \]

对于一个事件，当且仅当事件中某个样本点出现时，称为这个事件发生。
接着上面的例子，当扔骰子扔出数字 \(5\) 这一样本点时，事件 “扔出的点数为奇数” 发生了。

当然，由于随机试验 “每一次实验总是会恰好出现一种结果”，也就是说在 \(\Omega\) 中必然有一个样本点发生，因此我们称 \(\Omega\) 为 必然事件。对应的，由于随机实验不可能一个样本点也不发生，因此 \(\varnothing\)，也就是“一个样本点也不发生” 这件事件是不可能的，我们称其为 不可能事件。
这两种事件没有随机性，我们把它两个独立出来。

2. 事件之间的关系和运算

从上面的定义可以看出，随机事件本质是集合，那么多个事件之间有没有集合关系呢？
对于两个事件 \(A,B\)，它们有如下的关系：

• 如果事件 \(A\) 发生，则事件 \(B\) 一定发生，则称 \(A\) 包含于 \(B\)，或 \(B\) 包含（没有“于”） \(A\)。用符号写作 \(A\subseteq B\)，\(B\supseteq A\)。
• 事件 \(A\) 和事件 \(B\) 中至少一个发生，这种事件叫做 并事件，也叫和事件，写作 \(A\cup B\)，也可以写作 \(A+B\)。
• 事件 \(A\) 和事件 \(B\) 中必须同时发生，这种事件叫做 交事件，也叫积事件，写作 \(A \cap B\)，也可以写作 \(AB\)。
• 事件 \(A\) 和事件 \(B\) 不可能同时发生，此时称这两种事件 互斥，或 两事件互为互斥事件，显然此时 \(AB=\varnothing\)，也可倒推。
• 不是事件 \(A\) 发生就是事件 \(B\) 发生，此时称这两种事件 互为对立。例如扔硬币，正面向上和反面向上这两种事件就互为对立。此时 \(A+B=\Omega\)，\(AB=\varnothing\)，也可倒推。
  显然，互为对立的两种事件一定互斥。
  对于一个事件 \(A\)，它的对立事件也可以写成 \(\overline{A}\)

概率的表示

用 \(P\) 表示一个事件的概率，即事件 \(A\) 发生的概率为 \(P(A)\)。

3. 古典概率模型 （古典概型）

对于一个随机实验，如果它满足：

• 样本点的个数有限
• 每个样本点发生的可能性相等

那么这个实验就是古典概型实验。
如果这个实验是古典概型实验，样本空间有 \(n\) 各样本点，事件 \(A\) 有 \(k\) 个样本点，此时：

\[P(A)=\frac{k}{n} \]

4. 概率的基本性质

1. 对于任意事件 \(A\)，都有 \(P(A)\ge 0\)。
2. \(P(\Omega)=1\)，\(P(\varnothing)=0\)。
3. 对于事件 \(A,B\)，如果 \(AB=\varnothing\)，即 \(A,B\) 互斥，则 \(P(A+B)=P(A)+P(B)\)。
4. 对于事件 \(A,B\)，如果 \(A+B=\Omega,AB=\varnothing\)，即 \(A,B\) 互为对立，则 \(P(A+B)=1=P(A)+P(B)\)。
5. 对于事件 \(A,B\)，如果 \(A\subseteq B\)，即 \(A\) 包含于 \(B\)，则 \(P(A)\le P(B)\)。
6. 在同一个随机实验中，对于任意两个事件 \(A,B\)，\(P(A+B)=P(A)+P(B)-P(AB)\)，其实就是容斥原理。

5. 事件的相互独立性

对于两个事件 \(A,B\) 如果 \(P(AB)=P(A)P(B)\)，则称事件 \(A,B\) 相互独立，简称为独立。
如果 \(P(AB)=P(A)P(B)\)，可以推得以下三式成立：

• \(P(\overline{A}B)=P(\overline{A})P(B)\).
• \(P(A\overline{B})=P(A)P(\overline{B})\).
• \(P(\overline{AB})=P(\overline{A})P(\overline{B})\).
  详细证明如下：

6. 条件概率

设 \(A,B\) 为两个随机事件，且 \(P(A)>0\)，定义：

\[P(B\mid A)=\frac{P(AB)}{P(A)} \]

为 “在 \(A\) 事件发生的前提下，\(B\) 事件发生的概率”。

对于上面的公式，显然有：

\[P(\Omega\mid A)=1 \]

如果 \(B,C\) 两事件互斥，则：

\[P(B+C\mid A)=P(B\mid A)+P(C\mid A) \]

如果 \(B,\overline{B}\) 互为对立事件，则：

\[P(\overline{B}\mid A)=1-P(B\mid A) \]

将上面的公式稍作变形即可得到：

\[P(AB)=P(A)P(B\mid A) \]

7. 全概率公式与贝叶斯公式

（以下图片来自此视频，支持原创！）
以上公式都是研究两个事件之间的概率问题，如果是多个事件对应的多个概率呢？
首先我们设这里有 \(A_1,A_2\cdots A_n\) 个互斥事件，每种事件都有可能使 \(B\) 事件发生，如下图：

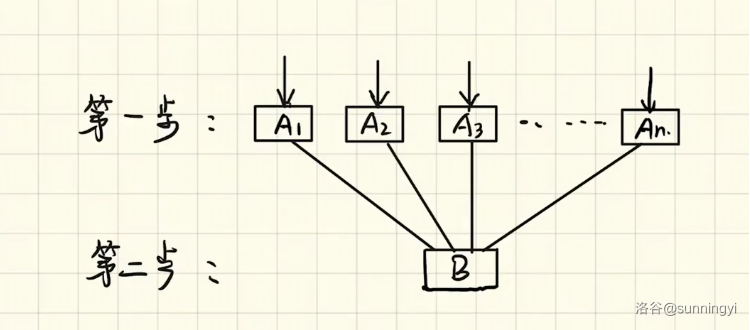
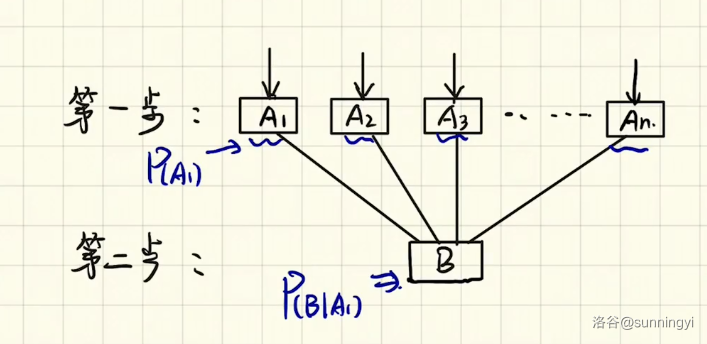
此时定义对于事件 \(A_i\)，其发生的概率为 \(P(A_i)\)，如果“在事件 \(A_i\) 发生的基础上 \(B\) 事件发生”，此时的概率可以用条件概率表示为 \(P(B\mid A_i)\)（请注意，对于每个 \(A_i\)，这个概率可能是不同的）。
那么，“发生了事件 \(A_i\) 又发生了事件 \(B\)”，这个事件的概率就是一个简单的积概率，也就是 \(P(A_i)P(B\mid A_i)\)。


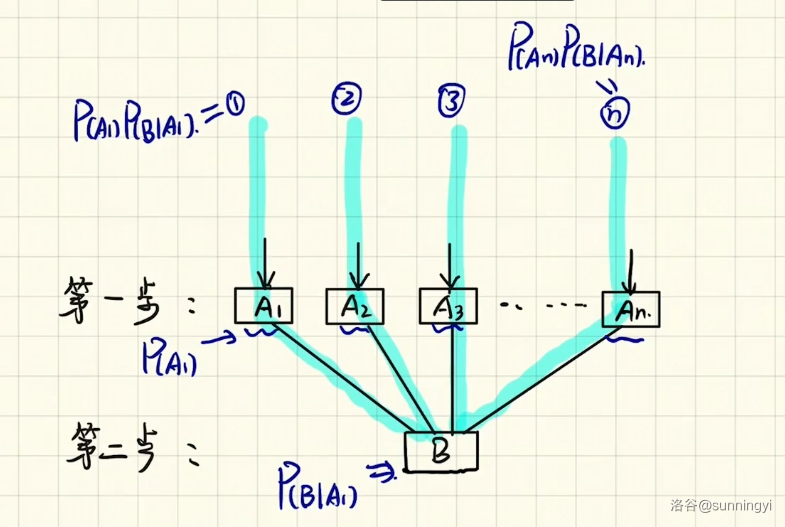
因为每个 \(A_i\) 和其他事件之间都是互斥的，因此 在事件 \(A_i\) 发生的基础上 \(B\) 事件发生” 这个事件肯定也是互斥的。

那么，既然在 \(A_i\) 这一条路径上完成 \(B\) 的概率是 \(P(A_i)P(B\mid A_i)\) ，由于这些事件是两两互斥的，因此根据概率的基本性质第三条，我们有：

\[P(B)=\sum_{i=1}^n P(A_i)P(B\mid A_i) \]

这就是 全概率公式

如果我们已知 \(P(B)\) 也就是 \(B\) 事件发生的概率，有多大的可能是从 \(A_i\) 这条路径实现的呢？这也就是求：“在事件 \(B\) 发生的基础上 \(A_i\) 事件发生”的概率”。

既然在 \(A_i\) 这一条路径上完成 \(B\) 的概率是 \(P(A_i)P(B\mid A_i)\)，又已知全部路径的概率和（即 \(P(B)\)，上面的全概率公式就是所有路径概率的和），两者相除不就可以了？
于是有：

\[P(A_i\mid B)=\frac{P(A_i)P(B\mid A_i)}{P(B)}=\frac{P(A_i)P(B\mid A_i)}{\sum_{i=1}^n P(A_i)P(B\mid A_i)} \]

这就是 贝叶斯公式。
试试这个题吧：洛谷 P8804.

迁移自洛谷