搜索专题

前言

骗分的神。

1. 深度优先搜索 DFS

这种搜索可以简单理解为 “一条路走到黑”，也就是程序会一直沿着某条路径向下扩展，一直走到边界条件限制其无法继续扩展为止。此后，程序会在原来的路径上从某条分支上继续走到黑。
这种搜索算法适用于解决方案数问题的暴力骗分。一般使用递归实现。
想当年作者天真的以为世界上只有这一种求解方格子最短路的算法
只讲这个比较简单，下面讲讲优化。

剪枝

通俗点说就是把搜索中一定不会达到目标的“路径”舍弃。由于 DFS 过程中形成的路径形似一根根树枝，因此这样的技巧被称作剪枝。
剪枝有许多情况，下面举一些例子：

可行性剪枝

搜索中的某些条件超出题目中的限制就没必要继续搜索了。如已经选择的物品个数比题目限制的多，搜索的深度过深，总和过大等。
这种剪枝比较容易实现，也比较容易想到。

最优性剪枝

这种剪枝尤其适合 DFS。由于其 “一条路走到黑” 的特性，某些路径可能先得到了一个到达目标条件的解。此时我们在其他情况的搜索中如果发现此时解已经比可能的解还要劣就没必要继续搜索了。

重复性剪枝

某些选择类搜索问题中可能出现选择元素重复的情况，例如如果在搜索中只关心元素种类不关心元素先后的情况。这时如果我们花些时间和空间判断一下选择的重复性并及时剪枝可能会有意想不到的优化。当然也可能一点都没有优化。
记忆化搜索就是一种重复性剪枝。

奇偶性剪枝

这种剪枝比较难应用。
一般要对搜索区域进行黑白染色，根据性质：走奇数会改变颜色，走偶数步则颜色不变。这样可以根据起电和终点颜色的不同和路径的长度来判断可行性。

迭代加深搜索

双向 DFS

IDA* 算法

回溯

2. 广度优先搜索 BFS

顾名思义，这种搜索以广为主，也就是在起点处尽量向所有可能的情况扩展，再在原来扩展出来的情况处二次扩展，重复此过程。
BFS 一般使用 while 循环和队列实现。
BFS 的一个突出特点是第一次到达结束状态的一定是整个转移状态的最优解。因此，BFS 常被用于图论的最短路算法中。

双向 BFS

普通的 BFS 是单向的，由于 BFS 的广度，其在进行多次扩展后的空降复杂度指数级增长，常会 MLE。这时使用双向 BFS 就会极大的缩小空间乃至时间使用。
想象下面的情况：有一起始状态和一目标状态，以及许多中间状态。使用 BFS 求解变换使两种状态相等的最优解，使用单向 BFS 的复杂度示意图如下：

优化后：

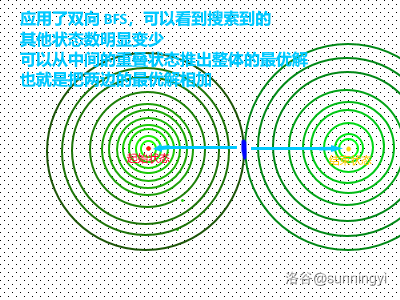
一般来说，两种状态之间的距离越远，优化效果越明显。

A* 算法

---

迁移自洛谷