逆序对专题

一个数组，只允许一次交换相邻的两个数，求使这个数组有序的最小交换次数？
这样的问题也就是在问：这个数组中的逆序对有多少。

逆序对的定义

对于一个数列 \(\{a_i\}\)，如果有 \(i<j\) 且 \(a_i>a_j\)，那么我们称 \(a_i\) 与 \(a_j\) 为一对逆序对。
例如 \((4,2),(198,45),(331,92),(514,114)\) 都是一些逆序对

1. 数据结构求法

由于这种方法仅需支持前缀求和，这里使用最易实现的树状数组。
考虑数组中的每一个数，与这个数构成逆序对的个数就是数组中在这个数之前且比这个数大的数的个数。
我们构建一个树状数组，每个下标 \(i\) 表示 \(i\) 在数组中出现的个数。
此时从左到右遍历整个数组，每遍历到一个数便将其对应的 \(i\) 值在树状数组上加一。完成后使用树状数组前缀求和的特性求解出 \(1\sim i\) 的值之和，这个和值即表示从数组开头到这个数的位置处所有小于等于这个数的数的个数和。
此时使用已经遍历过的数的个数减去这个和值就是从数组开头到这个数的位置处所有大于这个数的数的个数和。
很明显，这个和值就是和这个数构成逆序对的数量。将这个数累加到答案中。

时间复杂度 \(O(2n\log_2 n)\)，空间复杂度 \(O(\max a_i)\)
当 \(n\) 范围正常但有一些 \(a_i\) 特别大时，还需要对数组进行离散化处理，比较麻烦。

2. 归并排序求法

其实冒泡排序也可以求，但是太慢了。
这种方法无需在意 \(a_i\) 的大小。
归并排序使用了递归思想，即先排两边再合并。我们在两边进行合并时统计答案。
如图时归并排序时的一种情况：

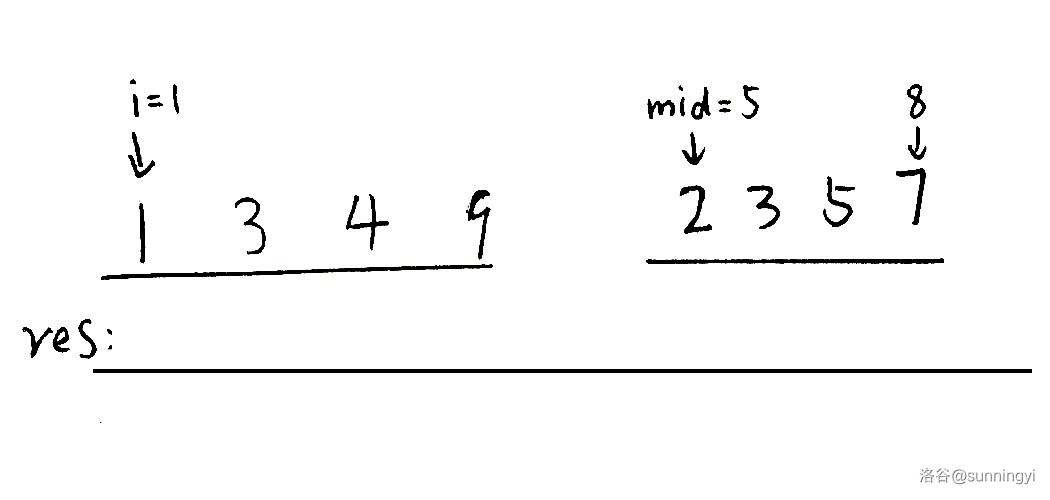
开始合并，左侧的 \(1\) 先被放入了结果数组中：

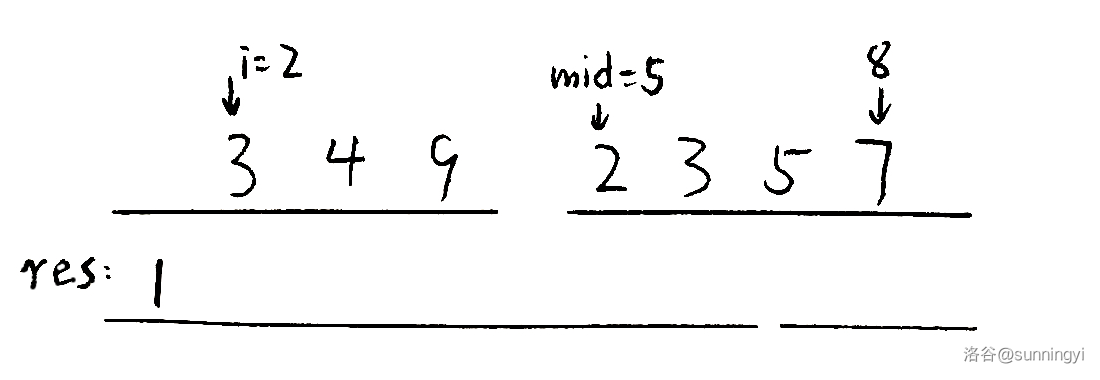
此时对于右侧的 \(2\)，它就可以和左边剩下的三个元素构成逆序对：

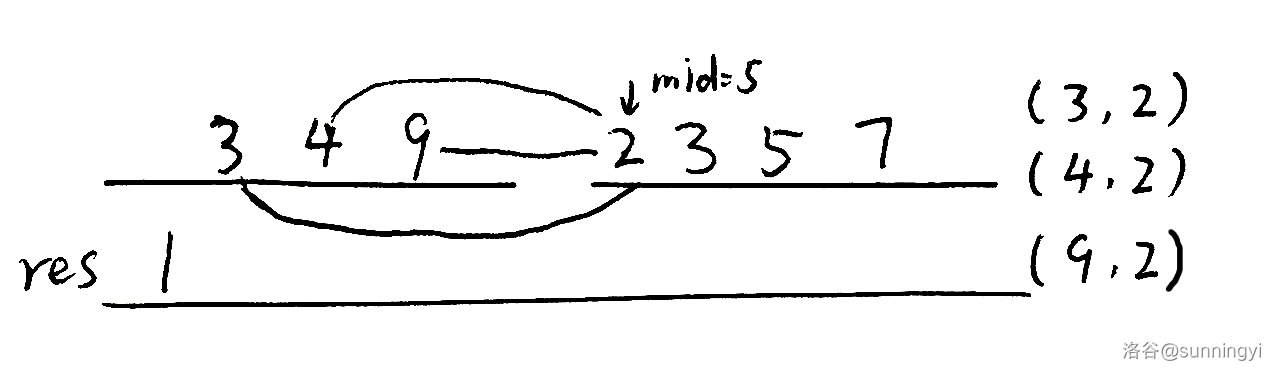
同理，当程序进行到放入右侧的 \(3\) 时，它也可以与左边剩下的两个元素构成两个逆序对：

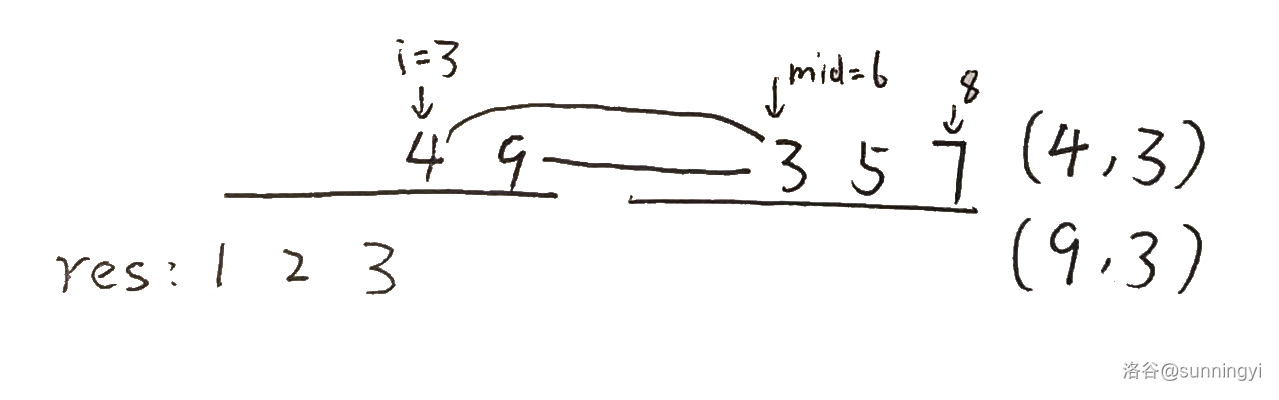
因此，当 \(mid\) 指向的右侧元素要被放入时，其与左侧元素可以构成逆序对的个数为：

\[\left\lfloor\frac{l+r}{2}\right\rfloor-i+1 \]

其中 \(l,r\) 分别表示这一次归并的数组的左右下标，对应上面的例子则 \(l=1,r=8\)。

这样，我们就在完成这一次归并的过程中计算出了这次归并中形成的逆序对个数，将这个数累加到答案中，当归并排序完成时即为逆序对个数。
你可能会问：照上面这种情况，\(1,3,4,9\) 形成的逆序对个数怎么计算？不要忘了，这是一个递归算法，当 \(1,3,4,9\) 与 \(2,3,5,7\) 进行归并时，其本身的逆序对个数已经被计算过了。
代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rd read()
ll read(){
	ll x=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
ll cnt=0;//逆序对数 
int a[1000005],res[10000005];
void mergesort(int l,int r){
	if(l==r)return;
	int mid=l+r>>1;//不同于例子中的 mid，这里的 mid 是不动的 
	mergesort(l,mid);
	mergesort(mid+1,r);
	int i=l,j=mid+1,k=l;
	while(i<=mid&&j<=r){
		if(a[i]<=a[j]){
			res[k++]=a[i++];
		}
		else{
			res[k++]=a[j++];//在归并时统计逆序对数量 
			cnt+=mid-i+1;
		}
	}
	//放完后数组里有落下的要记得放到结果数组里 
	while(i<=mid){// 
		res[k++]=a[i++];
	}
	while(j<=r){
		res[k++]=a[j++];
	}
	for(i=l;i<=r;i++){//重置原数组 
		a[i]=res[i];
	}
	return;
}
int main(){
	
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		a[i]=rd;
	}
	mergesort(1,n);//调用，对 (1,n) 进行归并排序 
	cout<<cnt;
	
	return 0;
}

这个算法的时间复杂度是 \(O(n\log_2 n)\)，空间复杂度是 \(O(n)\)。

---

迁移自洛谷