容斥原理

前言

又有好多题目变得简单了。

1.是什么

来一个经典的例子：想象一个班级里的所有同学，每个同学至少喜欢一种科目。一共有语文和数学两种科目，已知喜欢语文科目的人数（不一定只喜欢语文）和喜欢数学科目的人数（也不一定只喜欢数学）以及两科都喜欢的人数，问这个班里有多少人？
把 “喜欢语文科目的人” 和 “喜欢数学科目的人” 分别看作两个集合 \(C,S\)，则班级人数就是 \(|C\cup S|\)。其中 \(\cup\) 为集合的并运算，\(||\) 表示集合中元素的个数。
把这个情景表示为一个 Venn 图：

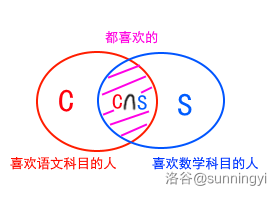
那么可以这样求解 \(C\cup S\)：

\[|C\cup S|=|C|+|S|-|C\cap S| \]

很容易理解：首先计算 \(C+S\)，那么中间也就是 \(C\cap S\) 的部分一定被算了两次，还要再减去一个 \(C\cap S\) 才是正确答案。

科目只有两个的情况很好办，那么如果有三科，九科，\(n\) 科的情况又怎么处理呢？
这就要用到容斥原理的知识了：

设 \(U\) 中元素有 \(n\) 种不同的属性，而第 \(i\) 种属性称为 \(P_i\)，拥有属性 P_i 的元素构成集合 \(S_i\)，那么

\[\begin{aligned} \left|\bigcup_{i=1}^{n}S_i\right|=&\sum_{i}|S_i|-\sum_{i<j}|S_i\cap S_j|+\sum_{i<j<k}|S_i\cap S_j\cap S_k|-\cdots\\ &+(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^{m}S_{a_i}\right|+\cdots+(-1)^{n-1}|S_1\cap\cdots\cap S_n| \end{aligned}\]

即

\[\left|\bigcup_{i=1}^{n}S_i\right|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^mS_{a_i}\right| \]

以上是 OIwiki 中的对容斥原理的描述，对我们蒟蒻来说看起来十分ex，用通俗的语言来描述一下它：
已知现在有 \(n\) 个集合，求他们的并集的元素数量，记这个并集数量为 \(|B|\)。
此时我们从这 \(n\) 个集合中不关心顺序地依次选出 \(1,2\cdots n\) 个集合，求出这些集合的交集，记这个交集内的元素数量为 \(|P|\)。
当选出集合的数量为奇数时，\(|B|=|B|+|P|\)。
当选出集合的数量为偶数时，\(|B|=|B|-|P|\)。
都选完一遍后 \(|B|\) 即为答案。
关于证明

2. 例题们

范围内可被任意给定质数整除的数的个数

已知正整数范围 \(1\sim n\)，给定 \(m\) 个质数，求 \(1\sim n\) 中可以同时被 \(a_1,a_2,\cdots,a_m\) 其中一个数整除的数的个数。
容斥最经典的题目，首先来看怎么容斥。
我们知道，在 \(1\sim n\) 中，能被 \(a\) 整除的数的个数为 \(\left \lfloor \frac{n}{a} \right \rfloor\)。
但是，如果我们直接计算每一个 \(\left \lfloor \frac{n}{a_i} \right \rfloor\) 并把他们相加，很明显会出现许多的重复。
那么怎么办？别忘了容斥原理！
使用容斥原理前，我们要知道：如何求多个正整数都可以同时整除的数的数量？（也就是求多个数的交集）。
对于两个正整数 \(a_1,a_2\)，显然他们在 \(1\sim n\) 中可以被同时整除的数的个数为 \(\left \lfloor \frac{n}{a_1a_2} \right \rfloor\)。
接下来只要使用容斥原理的套路枚举并统计答案就可以了。
在枚举时有个 trick，由于我们枚举集合时不关注顺序，之前枚举的方法诸如 DFS 全排列等记录枚举的集合是否相同比较不便，因此我们想到用二进制。
使用二进制数每一位的 \(0/1\) 来表示这个集合选还是不选，那么 \(n\) 个集合的全部情况个数就是 \(2^{n}-1\) 个。
因此，我们只要从 \(1\) 枚举到 \(2^n-1\)，将枚举到的正整数转换成为二进制，根据二进制的 \(0/1\) 情况选定集合，即可不重不漏的考虑所有情况。
使用二进制枚举情况也算是一个常用的 trick 了，最经典应用的就是状压 DP。
代码如下：

#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
	ll x=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
ll num[100];
int main(){

	ll n,m;
	cin>>n>>m;
	for(int i=0;i<m;i++){
		cin>>num[i];
	}
	ll ans=0;
	for(int i=1;i<(1<<m);i++){//二进制枚举情况
		ll cnt=0,ct=1;//记录选入的集合个数和数值乘积
		for(int j=0;j<m;j++){
			if((i>>j)&1==1){
				cnt++;
				ct*=num[j];
				if(ct>n){
					ct=-1;
					break;
				}
			}
		}
		if(ct==-1)continue;
		if(cnt&1==1){
			ans+=n/ct;// n/ct 便是这些集合的交集的元素个数
		}
		else{
			ans-=n/ct;
		}
	}
	cout<<ans;
	
	return 0;
}

鲜花

作者一开始编写代码与暴力程序对拍测试时发现总是不对，直到搜索了原题才发现要保证输入都是素数。
为什么呢，以 \(4,8\) 在大于 \(1\) 且小于等于 \(32\) 的正整数范围为例，实际上可以被 \(4,8\) 同时整除的数有 \(8,16,24,32\) 总共 \(4\) 个。但如果按照公式来算就只有 \(\left \lfloor \dfrac{32}{4\times 8} \right \rfloor =1\) 个了。
造成这样问题的原因是：可能有些数在小于两数乘积的范围内，且也可以被两数同时整除。
而对于质数：能被同时整除的数一定大于等于两数的乘积，因为除了两数本身和 \(1\) 外，这两数的乘积无法被任何正整数整除。

第 \(k\) 个互质的正整数

Luogu P1592 互质。
本来是个找规律题，但是容斥也可以做。
首先考虑互质是什么概念，大了说就是两者的最大公因数为 \(1\)，从质因数分解的角度看就是两个数的质因数分解中没有相同的质数。
那么也就是说：可以被这个数的质因数分解中的任意一种质数整除的数一定不与它互质。
这像不像上面的例题？也就是说，只要我们给定一个上界，就可以用容斥快速求解出 “被这个数的质因数分解中的任意一种质数整除的数” 的个数。
那么反过来，“不可以被这个数的质因数分解中的任意一种质数整除的数” 是什么数呢？很明显，都是与这个数互质的数。
由于与这个数互质的数在区间内的个数是随着区间的增大而单调不降地增大的，因此我们可以使用二分来确定那个第 \(k\) 个整数的值。
代码如下：

#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
	ll x=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
bool is_prime[1000005];
int prime_list[1000005];
int num=0;
//欧拉筛法求质数，由于质数集都被放在了 prime_list 数组中且单调递增，因此可以十分方便的调用
void Euler_Sieve(int n){
	memset(is_prime,1 ,sizeof is_prime); 
	is_prime[1]=0;
	for(int i=2;i<=n;i++){
		if(is_prime[i])prime_list[++num]=i;
		for(int j=1;j<=num&&i*prime_list[j]<=n;j++){
			is_prime[i*prime_list[j]]=0;
			if(i%prime_list[j]==0)break; 
		}
	}
}
int zys[30];//质因数 (zys) 分解的结果
int cnt=-1;
ll n,k;
bool check(ll lb){//二分答案的模板，这里 lb 指 1 ~ lb 这个范围
	ll ans=0;
	for(int i=1;i<(1<<cnt);i++){//容斥计算可以被任意一个整除的数的个数
		ll cnti=0,ct=1;
		if(1){
			for(int j=0;j<cnt;j++){
				if((i>>j)&1==1){
					cnti++;
					ct*=zys[j];
					if(ct>lb){
						ct=-1;
						break;
					}
				}
			}	
		}
		if(ct==-1)continue;
		if(cnti&1==1){
			ans+=lb/ct;
		}
		else{
			ans-=lb/ct;
		}
	}
	ans=lb-ans;//互质的数的个数只需减去总数
	if(ans>=k)return 1;//取多了，范围往小缩
	else return 0;//取少了
}
int main(){

	cin>>n>>k;
	Euler_Sieve(n); 
	int nb=n;
	num=1;
	while(nb!=1){//质因数分解
		while(nb!=1&&nb%prime_list[num]==0){
			nb/=prime_list[num];
			if(cnt==-1||zys[cnt]!=prime_list[num]){
				zys[++cnt]=prime_list[num];
			}
		}
		num++;
	}
	ll l=1,r=1e16;
	cnt++;
	while(l<r){//二分模板
		ll mid=l+r>>1;
		if(check(mid))r=mid;
		else l=mid+1;
	}
	cout<<l;
	
	return 0;
}

虽然容斥的时间复杂度是 \(O(2^n)\) 的，但是可以用贪心证明在本题的数据范围 （\(1 \leq n \le 10^6\)，\(1 \leq k\le 10^8\)） 里，任何整数拥有的质因数种类不会超过 \(10\) 个。

规定上界的不定方程整数解计数

CF451E Devu and Flowers
【好题选讲】CF451E Devu and Flowers

---

迁移自洛谷