Trie 树

前言

作者喜欢读 T R I E 树，而不是 try 树。

1. Trie 树是什么

Trie 树，中译 字典树，一种树形数据结构。它将我们要处理的字符串通过拆分的方式存储在了一课树上，查询时可以像字典一样依次从树根向下寻找，因此得名。
比较特殊的是：在 Trie 树中，节点一般不存储值，而是连接各点的边存储着值。

2. 怎么构建 Trie 树

Trie 采用存儿子的方式构建树。在下文的说明和程序中，我们用 \(son[id][v]\) 来表示编号为 \(id\) 的节点通过代表 \(v\) 的边连接的节点编号。
当我们想把字符串构建到 Trie 树上时，通常从左到右提取字符构建。对于每一个字符：

1. 当其所在的节点没有代表这个字符的连接下一个节点的边时，新建一个节点并将所在的节点与这个节点用代表这个字符的边相连。
2. 当其所在的节点有代表这个字符的连接下一个节点的边时，去往对应的下一个节点，取字符串的下一个字符，重复上述过程。
3. 当一个字符串构造完成后，通常在完成的那个节点上打一个标记，以便之后对 Trie 的使用（这里根据题目情况处理，有可能不需要打任何标记，有可能经过的每个节点都要打标记）。

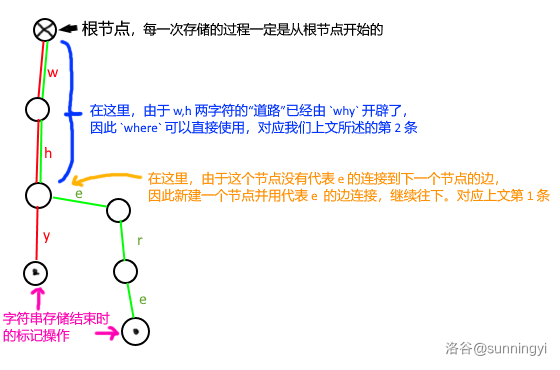
字符描述太枯燥了，来看一个具体的例子：

在图中，我们将字符串 \(\texttt{why}\) 和 \(\texttt{where}\) 先后构造入同一个 Trie 中。

理论讲完了，来看看代码：

ll rf[256];//某个字符代表的数，类似于哈希表 
int son[N][mcc];//Trie 树的主要数组 
int cnt[N];//标记数组 
ll id=0;//节点编号 
void build(string s){
	int p=0;//当前道路哪个节点，0 号是根节点 
	for(int i=0;i<s.size();i++){//从左到右提取字符 
		if(!son[p][rf[s[i]]]){//如果没有对应的边 
			son[p][rf[s[i]]]=++id;	//新建一个节点并用边相连 
			p=son[p][rf[s[i]]];//去那个新建的节点继续 
		}
		else
			p=son[p][rf[s[i]]];	//有对应的边，直接继续 
	}
	cnt[p]++;//构建完成后，在结束节点打标记 
}

3. Trie 树有什么用

首先来看看最基础的：查找一个字符串在之前给定的输入中是否出现过，出现了几次。
我们把给定的输入全都放到一个 Trie 中。当查找是否出现时，还是将字符串从左到右分离，如果有代表这个字符的边，去下一个节点，如果没有，直接报告这个字符串未曾出现过。
但是，当匹配结束的节点未被打标记时，也代表这个字符串在先前未出现，仅是某个字符串的前置子串。
因此可以写出如下代码：

ll query(string s){
	int p=0;
	ll ans=0;
	for(int i=0;i<s.size();i++){
		if(!son[p][rf[s[i]]])return 0;
		p=son[p][rf[s[i]]];
	}
	if(cnt[p]==0)
		return 0;
	else
		return cnt[p];
}

找前置子串是否出现和出现次数比上面还简单，只是要注意此时要把经过的所有节点都打一次标记，这样才能统计某一种子串到底出现了多少次。代码不再写了。

Trie 树还与异或运算有一些关系，例如下面这道题：
LOJ 10050 The XOR Largest Pair

在给定的 \(n\) 个正整数中选出两个进行异或运算，得到的结果最大是多少？

既然是异或，那么肯定与数的二进制有关，于是我们想到：将这些数转换成二进制的 \(01\) 序列，存入 Trie 中。
问题来了，怎样存呢？是低位到高位存，还是从高位到低位存？
事实上，我们应从高位到低位存，因为这样我们可以用贪心很方便的求得结果。
先来讲讲怎样贪心：由异或的性质，我们再枚举二进制数位时总要让两个数位不相同——不相同为 \(1\)，这样才能让异或的结果更大。
因此，我们枚举每一个数，使它从高位到低位匹配 Trie 上每个数位尽可能不同的 \(01\) 序列，在匹配过程中计算异或结果。此时的异或结果就是这个数与上文所有数中选一个数的异或最大值。想要知道两两异或的最大值，只需要把所有数枚举一遍。
那么，为什么这样贪心对呢？因为二进制表示的数有这样的特点：

\[(1000\cdots000)_2>(0111\cdots111)_2 \]

也就是说：在两个二进制数位数相同的情况下，即使这个二进制数只有最高位取 \(1\)，也要比除了最高位都取 \(1\) 的二进制数大。
因此，我们贪心时总让高位先变成 \(1\)，这样，即使下面的低位都可以变成 \(1\)，也不会让答案更优。即：从最高位贪心总是不劣于其他答案，符合贪心的要求。
看看代码：

#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
	ll x=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
const int N=100005*31;
int id=0;
int son[N][2];
void insert(int n){//从高位到低位将数字转换为二进制并放入 Trie 中 
	int p=0;
	for(int i=31;i>=0;i--){
		int dig=(n>>i)&1;
		if(son[p][dig]==0){
			son[p][dig]=++id;
			p=son[p][dig];
		}
		else{
			p=son[p][dig];
		}
	}
}
ll query(int n){
	int p=0;
	int res=0;
	for(int i=31;i>=0;i--){
		int dig=(n>>i)&1;
		if(son[p][!dig]!=0){//如果有不同的位 
			p=son[p][!dig];
			res+=(1<<i);//这一位异或后一定是 1，把这一位计入答案中 
		}
		else{
			p=son[p][dig];//如果没有就继续往下 
		}
	}
	return res;//返回答案 
}
int ng[100005];
int main(){

	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		int num;
		cin>>num;
		insert(num);
		ng[i]=num;
	}
	ll ans=0;
	for(int i=1;i<=n;i++){//枚举每一个数，求最大值 
		ans=max(ans,query(ng[i]));
	}
	cout<<ans;

	return 0;
}

Trie 也在 AC 自动机中有应用，详见这里。

迁移自洛谷