矩阵复数和向量

前言

FFT 的前置知识。

1. 矩阵

本质上是一个数表，类似于二维数组。

1.1 \(\LaTeX\)

圆括号矩阵

$$
\begin{pmatrix}
    a & \dots & b\\
    \vdots & \ddots & \vdots\\
    c & \dots & d\\
\end{pmatrix}
$$

\[\begin{pmatrix} a & \dots & b\\ \vdots & \ddots & \vdots\\ c & \dots & d\\ \end{pmatrix} \]

方括号矩阵

$$
\begin{bmatrix}
    a & \dots & b\\
    \vdots & \ddots & \vdots\\
    c & \dots & d\\
\end{bmatrix}
$$

\[\begin{bmatrix} a & \dots & b\\ \vdots & \ddots & \vdots\\ c & \dots & d\\ \end{bmatrix} \]

大括号矩阵

$$
\begin{Bmatrix}
    a & \dots & b\\
    \vdots & \ddots & \vdots\\
    c & \dots & d\\
\end{Bmatrix}
$$

\[\begin{Bmatrix} a & \dots & b\\ \vdots & \ddots & \vdots\\ c & \dots & d\\ \end{Bmatrix} \]

竖线矩阵（行列式）

$$
\begin{vmatrix}
    a & \dots & b\\
    \vdots & \ddots & \vdots\\
    c & \dots & d\\
\end{vmatrix}
$$

\[\begin{vmatrix} a & \dots & b\\ \vdots & \ddots & \vdots\\ c & \dots & d\\ \end{vmatrix} \]

1.2 矩阵的表示与比较

一般用一个大写字母加上角标来表示一个矩阵，如：

\[A_{m\times n} \]

表示一个 \(m\) 行 \(n\) 列的矩阵 \(A\)。

同型矩阵

如果两个矩阵的行数，列数均相等，我们称这两个矩阵为同型矩阵。

相等矩阵

两个矩阵是同型矩阵，且对应位置的元素均相等。

1.3 矩阵的运算

加法

前提：两个矩阵是同型矩阵。
将两个矩阵的对应位置相加，得到的新矩阵就是这两个矩阵的和。
例：计算：

\[\begin{pmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ \end{pmatrix}+ \begin{pmatrix} 1 & 1&1\\ 2&2&2\\ \end{pmatrix}\]

结果为：

\[\begin{pmatrix} 2&3&4\\ 6&7&8\\ \end{pmatrix}\]

矩阵的加法满足交换律、结合律，即：

\[A+B=B+A\\ (A+B)+C=A+(B+C) \]

减法

前提：两个矩阵是同型矩阵。
将两个矩阵的对应位置相减，得到的新矩阵就是这两个矩阵的差。
例：计算：

\[\begin{pmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ \end{pmatrix}- \begin{pmatrix} 1 & 1&1\\ 2&2&2\\ \end{pmatrix}\]

结果为：

\[\begin{pmatrix} 0&1&2\\ 2&3&4\\ \end{pmatrix}\]

乘法

当一个数与矩阵相乘时，就是把矩阵每一个位置的值都乘以这个数。
这种运算具有交换律，结合律，分配律：

\[n\cdot A=A\cdot n\\ (n\cdot m) \cdot A=n\cdot (m \cdot A)\\ (n+m)A=nA+mA\]

当矩阵与矩阵相乘时，有前提条件：
对于矩阵 \(A_{a\times b}\) 和矩阵 \(B_{m\times n}\)，当 \(b=m\) 时，两者才能相乘。
两个矩阵相乘，用左侧矩阵中一行的某些数分别对应乘以右边矩阵一列中的数，将乘积相加作为新的矩阵中一个位置的值。
形式化的，对于两个矩阵 \(A_{i\times j}\) 和 \(B_{j\times k}\) 相乘，设新的矩阵为 \(C\)：

\[C_{i,k}=(A_{i,1},A_{i,2},\cdots,A_{i,j})与\begin{pmatrix} B_{k,1}\\ B_{k,2}\\ \vdots\\ B_{k,j}\\ \end{pmatrix}对应位置上的元素乘积之和\]

似乎很复杂，但定义是这样定的。
如果两个矩阵 \(A_{i\times j}\) 和 \(B_{j\times k}\) 相乘，则新的矩阵 \(C\) 是一个 \(i\) 行 \(k\) 列的矩阵。
特殊的，矩阵乘法不具有交换律，即对于矩阵乘法 \(AB\) 和 \(BA\)，可能有这样的三种情况：

交换前后不满足前提条件，无法进行乘法。
交换前后的乘积不是同型矩阵。
交换前后的乘积不一定相等。

矩阵乘法也具有如下的特殊性质：

如果 \(AB=0\)（即结果全是 \(0\) 的矩阵），无法得出 \(A=0\) 或 \(B=0\)。
如果 \(AB=AC,A\ne 0\)，无法得出 \(B=C\)。

矩阵乘法相对于普通乘法还有这样的性质：

结合律，即 \((AB)C=A(BC)\)
左右分配律，即 \(C(A+B)=CA+CB\)，\((A+B)C=AC+BC\)
不能将 \(C\) 与另一个矩阵的顺序调换，因为矩阵不具有交换律。

矩阵的转置

所谓转置，就是将矩阵的行和列互换。
用 \(A^T\) 来表示矩阵 \(A\) 的转置。
转置后，原来在 \(i,j\) 位置上的元素会到 \(j,i\) 去。
例如对于矩阵：

\[A=\begin{pmatrix} 1&2&3\\ 4&5&6\\ \end{pmatrix}\]

其转置为：

\[A^T=\begin{pmatrix} 1&4\\ 2&5\\ 3&6\\ \end{pmatrix}\]

1.4 特殊的矩阵

方阵：行数等于列数的方阵。
零矩阵：矩阵内的所有值都是 \(0\)，一般记作 \(O\)（大写的字母）。
单位矩阵：这个矩阵乘以任何一个矩阵都等于其本身。
单位矩阵是方阵，它的主对角线（左上到右下的对角线）上的值都是 \(1\)，其它值为 \(0\)。
一般将单位矩阵记作 \(E\)。一个 \(3\times 3\) 单位矩阵示例：
\[E=\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix}\]
对角矩阵：主对角线之外的元素全为 \(0\) 的方阵。
三角矩阵：主对角线一侧的元素全为 \(0\)（不含主对角线）的方阵。
对称矩阵：转置等于自己的矩阵（显然一定是方阵）。这样的矩阵中的元素以主对角线为对称轴对称。
行向量：只有一行元素的矩阵。
列向量：只有一列元素的矩阵。

1.5 计算机内表示矩阵

一般使用结构体或类来封装矩阵，在封装内重载运算符来让矩阵可以像普通的数一样加减乘除。
以下是在 C++ 中使用结构体封装的矩阵：

#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
	ll x=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
struct matrix{
	ll data[105][105];
	//矩阵的值 
	ll n,m;
	//矩阵的行列数,n 行 m 列。 
	
	matrix(){
		memset(data,0,sizeof data);
		//默认初始化为 0 矩阵 
	} 
	matrix(ll line,ll row,ll k){
		n=line;m=row;
		//调用构造函数自动构造为对角矩阵 
		if(m!=n){//如果不是方阵则无法构造，输出错误信息 
			cout<<"invaild initializing"<<'\n';
			return;
		}
		for(int i=1;i<=n;i++){
			data[i][i]=k;
		}
	}
	matrix operator+(const matrix &x)const{//重载 + 操作 
		if(x.m!=m||x.n!=n){
			cout<<"invaild addition operator"<<'\n';
			matrix res(1,1,1);
			return res;
		}
		matrix c;
		c.m=m;
		c.n=n;
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				c.data[i][j]=x.data[i][j]+data[i][j];
			}
		}
		return c;
	}
	matrix operator-(const matrix &x)const{//重载 - 操作 
		if(x.m!=m||x.n!=n){
			cout<<"invaild subtraction operator"<<'\n';
			matrix res(1,1,1);
			return res;
		}
		matrix c;
		c.m=m;
		c.n=n;
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				c.data[i][j]=data[i][j]-x.data[i][j];
			}
		}
		return c;
	}
	matrix operator*(const matrix &x)const{//重载 * 操作 
		if(m!=x.n){
			cout<<"invaild multi operator"<<'\n';
			matrix res(1,1,1);
			return res;
		}
		matrix c;
		c.n=n;
		c.m=x.m;
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				for(int k=1;k<=x.m;k++){
					c.data[i][k]+=data[i][j]*x.data[j][k];
				}
			}
		}
		return c;
	}
	matrix trans(){//转置函数 
		matrix c;
		c.n=m;
		c.m=n;
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				c.data[j][i]=data[i][j];
			}
		}
		return c;
	}
};
int main(){

	//testing
	
	matrix a,b;
	a.n=3;a.m=2;
	b.n=3;b.m=3;
	a.data[1][1]=1;a.data[1][2]=1;
	a.data[2][1]=5;a.data[2][2]=1;
	a.data[3][1]=1;a.data[3][2]=9;
	b.data[1][1]=9;b.data[1][2]=9;b.data[1][3]=9;
	b.data[2][1]=9;b.data[2][2]=9;b.data[2][3]=9;
	b.data[3][1]=9;b.data[3][2]=9;b.data[3][3]=9;
	
	matrix ans;
	ans=a.trans();
	
	for(int i=1;i<=2;i++){
		for(int j=1;j<=3;j++){
			cout<<ans.data[i][j]<<' ';
		}
		cout<<'\n';
	}
	
	//testing  
	
	return 0;
}

1.6 矩阵快速幂

详见我写的另一个专栏

2. 复数

2.1 一些定义

任何复数（complex number）都可以表示为 \(a+bi\) 的形式，其中 \(a,b \in \mathbb{R},b\ne 0\)。\(i\ (imaginary)\) 是人为定义的，\(i=\sqrt{-1}\)。
由定义可知 \(i^2=-1\)
一般用字母 \(z\) 来表示复数。
复数集 \(\mathbb{C}\) 是人类已经发现的最大的数集，其内分为实数集和虚数集。
虚数集又可细分为 纯虚数集，有如下关系：

所有数都可以表示为 \(a+bi\) 的形式。
当 \(b=0\) 时，这个数是实数。
当 \(a \ne 0,b \ne 0\) 时，这个数是虚数。
当 \(a=0,b\ne 0\) 时，这个数是纯虚数，纯虚数也是虚数。

对于一个复数 \(z=a+bi\)，\(a\) 叫做这个复数的实部，\(b\) 叫做这个复数的虚部。
对于两个复数，如果这两个复数的实部相等，虚部互为相反数，我们称这两个复数互为共轭复数。

2.2 复平面

类比于使用数轴来表示实数，由于一个复数的表示需要两个变量 \(a,b\)，我们将这两个变量组成点 \((a,b)\) 映射到一个坐标系中，这种表示复数的坐标系叫做 复平面。
在复平面中，人为规定 \(x\) 轴表示实部，\(y\) 轴表示虚部，如下图：

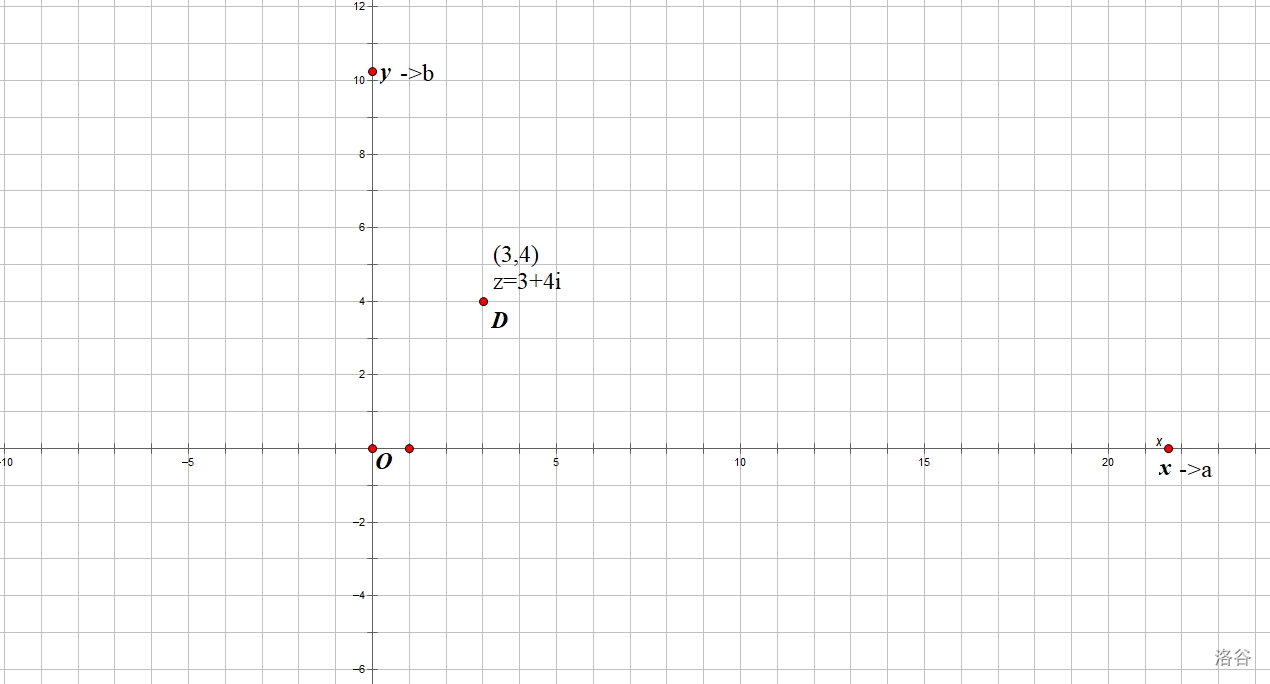
正如所有实数都可以在数轴上找到，所有虚数都可以在复平面上找到。
观察复平面可以发现：在 \(x\) 轴上的点表示实数，在 \(y\) 轴上的点表示纯虚数。

同样类比于在数轴上的点到原点的距离，我们把复数在复平面上对应的点到原点的距离叫做这个复数的模（模长），使用 \(|z|\) 表示。
复数的模可以简单地用勾股定理求出，即 \(|z|=\sqrt{a^2+b^2}\)

由于复平面上的点与复数是一一对应的，因此：

当两个点相同时，其所表示的复数相等。
当两个复数相等时，其在复平面内所对应的点也相同。

注意：复数之间一般不能比较大小。

2.3 四则运算

加法

两复数相加，分别把实部相加，虚部相加。
例：

\[\begin{aligned} z_1&=1+2i\\ z_2&=3+4i\\ z_1+z_2&=(1+3)+(2+4)i\\ &=4+6i \end{aligned}\]

复数与实数相加，只把实数与复数的实部相加。
复数的加法满足交换律和结合律。

减法

两复数相减，分别把实部相减，虚部相减。
例：

\[\begin{aligned} z_1&=1+2i\\ z_2&=3+4i\\ z_1-z_2&=(1-3)+(2-4)i\\ &=-2-2i \end{aligned}\]

复数与实数相减，只需按照顺序把实数与复数的实部相减。

乘法

两复数相乘，类似于多项式乘法。
例：

\[\begin{aligned} z_1&=1+2i\\ z_2&=3+4i\\ z_1z_2&=(1+2i)(3+4i)\\ &=3+4i+6i+8i^2\\ &=-5+10i \end{aligned}\]

实数与复数相乘，把实数分别与复数的实部与虚部相乘。
复数的乘法满足交换律，结合律，分配律。
有类似于实数的完全平方公式：

\[\begin{aligned} (a+bi)^2&=a^2+2abi+(b^2i^2)\\ &=a^2+2abi-b^2 \end{aligned}\]

平方差公式：

\[\begin{aligned} (a+bi)(a-bi)&=a^2-(b^2i^2)\\ &=a^2+b^2 \end{aligned}\]

在平方差公式中，我们发现参与计算的两个复数变成了实数，类比于根式的分母有理化，我们将这样的操作称为实数化。
实数化技巧常用于分母是复数的分数的化简中，下文除法运算中就有一例。

除法

一个复数除以另一个复数，相当于乘这个复数的倒数。
例：

\[\begin{aligned} z_1&=1+2i\\ z_2&=3+4i\\ z_1\div z_2&=z_1\times \frac{1}{z_2}\\ &=\frac{1+2i}{3+4i}\\ &=\frac{(1+2i)(3-4i)}{(3+4i)(3-4i)}（分母实数化）\\ &=\frac{11+2i}{25}\\ &=\frac{11}{25}+\frac{2}{25}i（化为一般形式）\\ \end{aligned}\]

实数除以复数和复数除以实数也是同理列出分数计算即可。

3. 平面向量

既有大小又有方向的量叫做向量。
向量可以使用一个带箭头的线段在几何上表示，如：

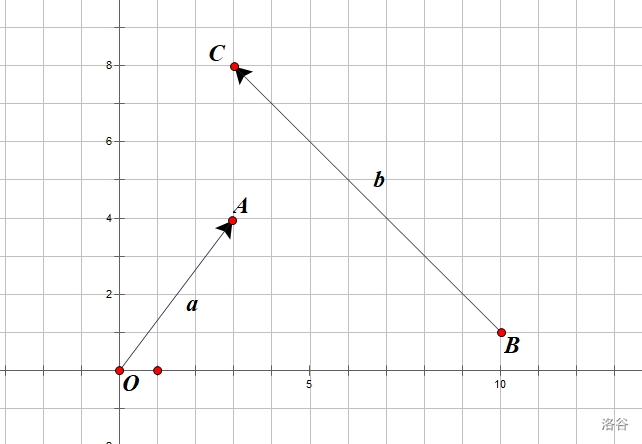
在图中，从 \(O\) 到 \(A\) 的带箭头的线段表示一个向量。
代数层面，我们用一个向量的起始点与结束点所代表的字母按顺序组合在一起，在上面加个从起始点到结束点的箭头来表示一个向量。
例如在上图中的两个向量可以表示为：

\[\overrightarrow{OA},\overrightarrow{BC} \]

               $$\overrightarrow{OA},\overrightarrow{BC}$$

注意：箭头指向左边的记法一般不常用。
像线段一样，我们也可以用一个小写字母表示一个向量。
例如在上图中的两个向量还可以表示为：

\[\vec{a},\vec{b} \]

                           $$\vec{a},\vec{b}$$

某一写书籍上常常用加粗的小写字母表示一个向量，常常不写箭头，但是手写体必须加箭头。

两个向量相等，代表两个向量的大小，方向相同。
反过来，只有两个向量的大小，方向同时相同时，两个向量才相等。
这里我们可以发现，两个向量是否相等，和他们的起始点没有关系，因此 向量可以任意平移。

3.1 细说向量的大小和方向

向量的大小叫做向量的模长，书写时在向量的两边加上类似于绝对值的符号，例如：

\[|\overrightarrow{OA}| \]

                        $$ | \overrightarrow{OA} | $$

表示向量 \(\overrightarrow{OA}\) 的模长。
向量的模长在坐标系中可以简单的用勾股定理求出。
有几个特殊的模长：

当一个向量的模长等于 \(1\) 时，我们把这样的向量称作 单位向量。
使用 \(\overrightarrow{e}\) 来表示单位向量。
注意：单位向量不只有一个。
当一个向量的模长等于 \(0\) 时，我们叫做 零向量 。
使用 \(\overrightarrow{0}\) 来表示零向量。
注意：零向量的方向是任意的。

正如平面几何中线的关系一样，平面向量也有一些位置关系：

两个向量垂直，记作 \(\overrightarrow{a}\perp \overrightarrow{b}\)。
两个向量平行，记作 \(\overrightarrow{a}\parallel \overrightarrow{b}\)。
由于向量可以随意平移，因此对于两个互相平行的向量，也可以说他们是共线的。
同理对于两个共线的向量，也可以说他们是平行的。
因此，两个向量平行和两个向量共线这两种称呼是等价的。

由于零向量可以表示任意方向，因此我们说零向量与任意向量都是平行的。
因此，向量之间的平行没有传递性，反例如下：
\(\overrightarrow{a}\parallel \overrightarrow{b}\) 且 \(\overrightarrow{b}\parallel \overrightarrow{c}\) ，但如果 \(\overrightarrow{b}\) 是零向量，那么 \(\overrightarrow{a}\) 和 \(\overrightarrow{c}\) 的方向就有可能不相等了，因此 \(\overrightarrow{a}\) 和 \(\overrightarrow{c}\) 不一定平行。

3.2 向量的运算

为了方便演示，运算配图在直角坐标系内进行，使用几何画板制图。

加法

因为向量可以随意平移，我们一般将两个向量平移到首位相接或起点相同来进行计算。
类似于力的合成，当两个向量共起点时，两者加法的答案为两向量做出的平行四边形，从起点开始的对角线上的另一点。
直观的用图描述：

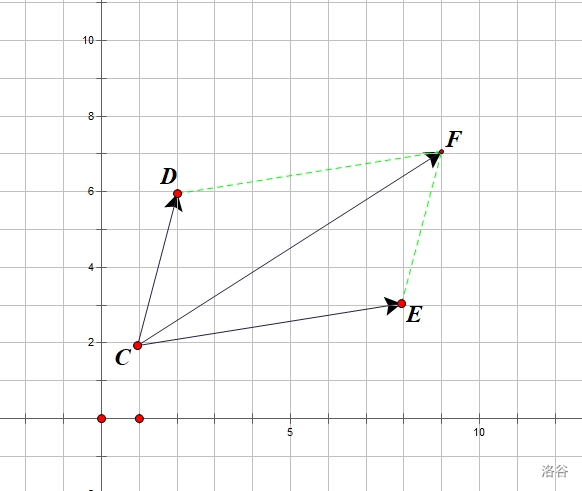
在上图中，\(\overrightarrow{CD}+\overrightarrow{CE}=\overrightarrow{CF}\)，可以看出，\(D,C,E,F\) 共同构成了一个平行四边形。
这样求解两向量和的方法我们称之为平行四边形法则。

但是当我们要求解多个向量的和时，每两个向量单独计算后在合并似乎有些麻烦，我们有第二种方法。
还是将向量平移，但

迁移自洛谷

posted @ 2025-02-04 13:28 hm2ns 阅读(137) 评论(0) 收藏举报

刷新页面返回顶部

hm2nsite

不过总有一天，我的心会游过夜晚，游到走累的你的身边