图的连通性与缩点思想
前言
RobertTarjan 就是神啊啊啊啊啊
Tarjan 不读 “塔剑” ,应读 “塔杨”。其中的 'j' 发 '也' 的音。
另一个例子:Mojang 不读 “魔将” ,应读 “魔样”。
rearranged on 2025 05 11
1. 有向图中的强连通分量
所谓连通图,就是一个图内所有点对之间都有一条路径。很明显,一个无向图一定是一个连通图。
对于一个有向图,我们把满足 图内所有点对之间都有一条路径 这样的有向图称为强连通图。
而连通分量可以简单理解为图中最大的连通子图。
在有向图中最大的连通子图我们叫它 强连通分量(Strongly Connected Components,SCC)。很明显,一个有向图中可能有多个 SCC。
1.1 找强连通分量
从定义来看找一个有向图中的 SCC 似乎是一件很困难的事,但是它存在时间复杂度仅为 \(O(n+m)\) 的算法。
Tarjan 算法
Tarjan 算法主要进行了一次 DFS,将图中的点按照遍历到的顺序编号,在向下搜索的过程中求解出每个点能到达的最小编号数。
求解出来的这两个东西有什么用呢?
我们将一个 SCC 中最早被搜索到的节点(也就是编号最小的节点)称为这个 SCC 的根。
那么我们可以发现,根能到达的最小编号数一定是他自己的编号。
原因很简单,如果根经过其他节点能到达比自己编号还小的节点,那么它就不是根了。
于是我们想到,在 DFS 过程中维护遍历到的顺序编号,维护每个点能到达的最小编号数。如果遍历完成回溯时发现一个点的顺序编号等于能到达的最小编号,那么这个点就是一个 SCC 的根。
那一个 SCC 中的其他点如何求解呢?我们使用一个栈来存储遍历的节点顺序,当找到一个根时,从栈顶到这个节点的所有节点就在同一个 SCC 里了。
作者不是很会证,关于这些结论的证明还是看OIwiki。
如何写 Tarjan 算法呢,由于数组有点多,我们先来明确一下:
int dfn[]每个点遍历到的顺序编号。int low[]每个点能到达的最小编号数。bool vis[]点是否在栈中,用来标记这个点是否在栈中。int id顺序编号。
第一步,我们将这个节点的 dfn 和 low 值均设置为 id,将此节点压入栈中,并将 vis 标记为 true。
第二步,遍历这个节点的所有邻接节点,此时分两种情况:
- 邻接节点没有被遍历到,也就是
dfn值为初始值,此时继续向这个节点 DFS,搜索完成后,更新low值。 - 邻接节点已被遍历到且还未被分到一个 SCC 中(也就是此节点还在栈中,
vis值为true),此时使用邻接节点的dfn值更新low值。
关于第二种情况,为何使用邻接节点的 dfn 值而不使用 low 值呢?因为此时邻接节点也在栈中,无法确定邻接节点的 low 是否被更新。
为何需要此节点未被分到一个 SCC 中呢?我们可以举出以下的反例:
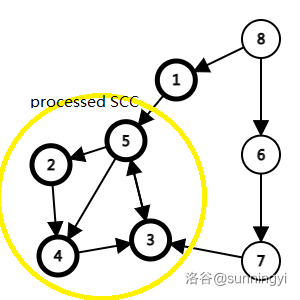
在上图中,每个点内的数字就是其 dfn 值(当然这样的 dfn 值顺序不可能出现,但我们仅需要知道黄圈中点的 dfn 值均小于右侧一条“链”上点的 dfn 值即可,这里仅是以举例为目的),黄圈中的点被先遍历并处理为了同一个 SCC,此时这些节点均不在栈中。
容易发现,整个图中 1 7 6 8 各自是一个 SCC。
如果此时 7 使用 3 更新了自己的 low 值。那么 7 的 dfn 便不再等于 low,此时便会漏掉 7,连带着还会漏掉其它点导致错误的答案。
第三步,遍历完成所有邻接点后,进行判断,如果此节点的 dfn 值等于其 low 值,那么便将从栈顶到这个节点的所有节点弹出并压入一个 SCC 中,不要忘记将 vis 标记为 false。
完整代码 \(+\) 注释:
code
Show me the code
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e4+5;
int n,m;
vector<int> edge[N];
int nodew[N];
int dfn[N],low[N];
bool vis[N];
int id=0;
stack<int> dfr;
vector<int> news[N];
void tarjan(int u){//u 为当前 DFS 到的节点
dfn[u]=low[u]=++id;//初值
vis[u]=1;//压入栈并标记
dfr.push(u);
for(int i=0;i<edge[u].size();i++){//遍历所有邻接点
int v=edge[u][i];
if(!dfn[v]){//情况 1
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]){//情况 2
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]){//是根
news[++cnt].push_back(u);//放入一个新的SCC中
while(dfr.top()!=u){//从栈顶到自己
news[cnt].push_back(dfr.top());//弹出并放入SCC
vis[dfr.top()]=0;//取消标记
dfr.pop();
}
dfr.pop();//把自己也弹出并取消标记
vis[u]=0;
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
u=rd;
v=rd;
edge[u].push_back(v);
}
for(int i=1;i<=n;i++){//有向图从一个点开始不一定可以遍历到全部边,因此要对每个便进行一次tarjan
if(!dfn[i])tarjan(i);//以 dfn 值判断其是否被遍历过
}
for(int i=1;i<=cnt;i++){//输出所有 SCC
for(int j=0;j<news[i].size();j++){
cout<<news[i][j]<<' ';
}
cout<<'\n';
}
return 0;
由于 Tarjan 算法仅对图进行了 DFS 操作,因此时间复杂度为 \(O(n+m)\),空间复杂为 \(O(n)\)。是一个非常优秀的算法。
1.2 缩点
在有向图中的缩点就是把一个有向图的所有强连通分量找出来并重新建图的过程。
新建的图以一个 SCC 作为一个点,且新图一定是一个 DAG。
关于第二个结论:如果几个强连通分量之间有环连接,那么他们几个一定可以组成一个更大的 SCC,这是在使用 Tarjan 算法时就可以求解出的,因此新图中不会有环,一定是个 DAG。
那么缩点有什么用呢,来看个例题:
洛谷 P3387 【模板】缩点
给定一个 \(n\) 个点 \(m\) 条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。
经过的点权值最大,我们不禁想到了拓扑排序,但是题目中没有说明给出的图一定是 DAG,如何下手呢?
注意到题目中有这样一句话:重复经过的点,权值只计算一次。
联系到上文的 SCC,我们想到:如果一个子图是一个 SCC,那么这个 SCC 大点的点权就是其内所有小点权值的和。
我们知道,缩点后新建的图一定是一个 DAG,这不是正方便了我们做拓扑排序吗?
于是我们使用 Tarjan 算法找出原有向图中的强连通分量,同时计算强连通分量的权值。
计算完成后,枚举所有点及其邻接点,根据两点属于的 SCC 的关系建新图,在新图上进行拓扑排序。
排序完成后,寻找所有结束点,找到最大值即为答案。
由于在新图中只需要知道两点属于的 SCC 的关系,我们可以使用染色法将同属于一个 SCC 的点染同一色,之后进行判断即可。
完整代码 \(+\) 注释,建议先看数组的意义以免乱套:
code
Show me the code
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e4+5;
int n,m;
vector<int> edge[N];//原有向图
int nodew[N];//每个点的点权
int dfn[N],low[N];//tarjan标准配置
bool vis[N];
int id=0;
stack<int> dfr;
int color[N];//每个节点属于的 SCC 的编号
int cnt=0;//SCC 计数器
vector<int> news[N];//新图
int newnodew[N];//新图中每个大点的点权
//拓扑排序标准配置
int din[N]; //每个大点的入度
queue<int> b;//入度为 0 的点
int res[N];//拓扑排序是每个点能获得最大权值
void tarjan(int u){
dfn[u]=low[u]=++id;
vis[u]=1;
dfr.push(u);
for(int i=0;i<edge[u].size();i++){
int v=edge[u][i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]){
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]){
color[u]=++cnt;//染色
newnodew[cnt]+=nodew[u];//计算大点权值
vis[u]=0;
while(dfr.top()!=u){
color[dfr.top()]=cnt;//染色
newnodew[cnt]+=nodew[dfr.top()]; //计算大点权值
vis[dfr.top()]=0;
dfr.pop();
}
dfr.pop();
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
nodew[i]=rd;
}
for(int i=1;i<=m;i++){
int u,v;
u=rd;
v=rd;
edge[u].push_back(v);
}
for(int i=1;i<=n;i++){
if(!dfn[i])tarjan(i);
}
for(int i=1;i<=n;i++){//枚举每个点
for(int j=0;j<edge[i].size();j++){//枚举每个点的邻接点
if(color[i]!=color[edge[i][j]]){//两个邻接点不属于同一个 SCC
news[color[i]].push_back(color[edge[i][j]]);//在两个 SCC 之间连边
//不要写成在两个原点之间连边!!!!!
din[color[edge[i][j]]]++;//入度增加
}
}
}
//以下是拓扑排序模版
for(int i=1;i<=cnt;i++){
if(!din[i]){
b.push(i);
res[i]=newnodew[i];
}
}
while(b.size()){
int cur=b.front();
b.pop();
for(int i=0;i<news[cur].size();i++){
int v=news[cur][i];
din[v]--;
res[v]=max(res[v],res[cur]+newnodew[v]);
if(din[v]==0){
b.push(v);
}
}
}
int ans=0;
for(int i=1;i<=cnt;i++){//计算答案并输出
ans=max(ans,res[i]);
}
cout<<ans;
return 0;
}
由此我们可以发现,缩点思想可以解决某些无顺序性和有传递性的的问题,比如在例题中点权无遍历的顺序关系。还有其他有传递性的问题比如“喜欢关系”“大小关系”等可能都可以进行缩点来快速解决。
1.3 鲜花
还有一个有趣的问题:在一个有向图中,在增加多少条边可以让其强连通?
我们先将原有向图缩点,那么其答案为缩点后入度为 0 的节点数和出度为 0 的节点数的最大值。
用数量少的一类点向数量大的一类点一一对应的连边,剩下的一些数量大的一类点在往内部随便连一些边就行了。
2. 无向图中的边双连通分量
在一张连通的无向图中,对于两个点 \(u\) 和 \(v\),如果无论删去哪条边(只能删去一条)都不能使它们不连通,我们就说 \(u\) 和 \(v\) 边双连通。
边双连通具有传递性,即,若 \(x,y\) 边双连通,\(y,z\) 边双连通,则 \(x,z\) 边双连通。
如果在一个无向图中有一个最大的子图,且这个图中对于任意一对节点 \(u\),\(v\) 都是边双联通的,那么我们称这样的图为边双连通分量(Edge - Double Connected Components,E-DCC),一般简称为“边双”。
如果在一个图中删去一条边可以让这个图不连通,我们把这样的边叫做割边,也叫桥。
2.1 找边双连通分量和桥
还是使用 Tarjan 算法:
因为在一个边双中不含桥,那么连接两个边双的一定是桥。
桥和 Tarjan 算法中的 dfn low 有什么关系呢?
我们知道,如果桥没了,无向图会分成两个连通块,这两个连通块中其中一个连通块里的所有点的 dfn 值一定大于 另一个的 dfn 值。
这也意味着:在不经过桥的情况下,一个边双内所有点的 low 值都等于这个边双内 dfn 值最小的点,我们还是把这个点称为根。
那么,根的 dfn 值也就等于 low 值了。
因此,我们只需把求解 SCC 的 Tarjan 稍作改动即可拿来求解边双。
怎样改呢?由于是无向边,我们不能让 DFS 到的点在回到他的父节点去,如果不这样,所有点的 low 值都是 1,答案就乱套了。
但是怎样 “不让 DFS 到的点在回到他的父节点去” 呢?一种错误的方法是:递归时标记这个节点的父节点是谁,在枚举邻接点的时候跳过。
为什么错呢?来看反例:
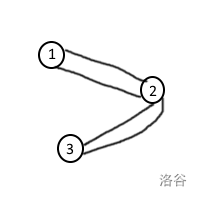
像这样的带有重边的无向图也是边双,因此,在存边时不应去掉重边;在使用 tarjan 算法时记录的不应是 从哪一个点过来,而是 到达这个点经过的边的反向边是哪条,以避免忽略了另一条无向边。
如何找出 “到达这个点经过的边的反向边” 呢,我们可以使用链式前向星存图,通过异或的性质快速找出反向边。
不过要注意:两者结合找反向边时,第一条边的下标应从 0 开始,正向边和反向边应挨在一起,一定要注意异或等位运算的优先级。
现在我们把边双找出来了,桥如何找呢?
因为桥是一条边,因此不应在 for 循环结束后进行寻找,在遍历邻接点的时候顺带找出即可。
我们把桥连接的两点中 dfn 较小的一方称为 “左边”,较大的一方称为 “右边”。
那么可以发现,右边的 low 值一定大于左边。因为如果右边可以回到左边甚至更往前的点,那么这条边就在一个环上,一定不是桥。
因此,我们在确定邻接点的 low 值后进行判断并标记桥即可。
要注意,由于是无向边,我们存图时存的正反边都要进行标记,这也可以用链式前向星快速解决。
完整代码 \(+\) 注释如下:
code
Show me the code
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=5e5+5;
const int M=2e6+5;
//链式前向星存图的板子
struct e{
int u;
int v;
int w;//边权
int nxt;//下一条边的下标
}edge[2*M];//要开 2*M
int _head[N];//注意将 _head 初始化为 -1
int cnt=-1; //边计数器
void add(int u,int v,int w){//加边函数
++cnt;
edge[cnt].u=u;
edge[cnt].v=v;
edge[cnt].w=w;
edge[cnt].nxt=_head[u];
_head[u]=cnt;
}
//tarjan 标准配置
int dfn[N],low[N];
bool vis[N];//这里其实不再需要 vis 数组,因为是对无向图,不存在有向图那样的特例了
//但是为了不记混还是写上为好
stack<int> s;
int id=0;
int col[N];//染色数组,这里没有用,因为用了vector存边双了
int ncc=0;//边双计数
vector<int> ne[N];//存边双
bool bri[2*M];//记录那条边是桥
void tarjan(int u,int fa){//fa指的是来到这个节点的边的下标,反向边就是 fa^1
dfn[u]=low[u]=++id;
s.push(u);
vis[u]=1;
for(int j=_head[u];j!=-1;j=edge[j].nxt){
int v=edge[j].v;
int w=edge[j].w;
if(j==(fa^1))continue;//如果是反向边直接跳过,注意加括号
if(!dfn[v]){
tarjan(v,j);//递归时标记反向边
low[u]=min(low[u],low[v]);
}
else if(vis[v]){
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]<low[v]){//处理完一个邻接点后判断这一条边是不是桥
bri[j]=1;//如果是则标记
bri[j^1]=1;
}
}
if(dfn[u]==low[u]){//判断是不是边双
ncc++;
col[u]=ncc;
vis[u]=0;
ne[ncc].push_back(u);
while(s.size()&&s.top()!=u){
int k=s.top();
s.pop();
ne[ncc].push_back(k);
vis[k]=0;
col[k]=ncc;
}
s.pop();
}
}
int main(){
fill(_head,_head+N-2,-1);//记得初始化为 -1
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
u=rd;
v=rd;
if(u==v)continue;//自环可以跳,重边不能跳
add(u,v,1);
add(v,u,1);
}
for(int i=1;i<=n;i++){
if(!dfn[i])tarjan(i,-1);
}
cout<<ncc<<'\n';
for(int i=1;i<=ncc;i++){//输出所有边双
cout<<ne[i].size()<<' ';
for(int j=0;j<ne[i].size();j++){
cout<<ne[i][j]<<' ';
}
cout<<'\n';
}
return 0;
}
板子题:
2.2 边双缩点
和强连通分量的缩点一样,就是把无向图中的边双找出来然后建新图的过程。
还没见到过这种题,先不写例题了。
边双缩点后的图一定是个树,因为有环的几个点一定会被缩到一个边双里去,因此缩点完的图一定是树。
这个树上的边就是这个无向图的桥。
那么加入多少条边会让整个图称为一个边双呢?答案是 \((\)这个树上所有度为 \(1\) 的结点个数 \(+1) \div 2\)。
这个树上所有度为 \(1\) 的结点 就是这个树的叶子,叶子之间可以两两连接形成环进而变成边双,于是可以把这些点两两连接起来,但是可能有一个点无法找到另一个叶子,那么就往树里任意一个点连一条边就好了。
3. 无向图中的点双连通分量
在一张连通的无向图中,对于两个点 \(u\) 和 \(v\),如果无论删去哪个点(只能删去一个,且不能删 \(u\) 和 \(v\) 自己)都不能使它们不连通,我们就说 \(u\) 和 \(v\) 是点双连通的。
要注意,点双连通没有传递性,因为有可能传递的是个割点。
在一个无向图最大的子图,图中对于任意一对节点 \(u\),\(v\) 都是点双联通的,那么我们称这样的图为点双连通分量(Vertex - Double Connected Components,V-DCC),一般简称为“点双”。
3.1 找点双连通分量和割点
还是用钳制的思想,low[v]>=dfn[u] 代表 \(v\) 没法在不通过 \(u\) 的情况下去之前的任何一个点,这意味着 \(v\) 及其从属的点的命运只由 \(u\) 掌控,\(u\) 一旦没有那么 \(v\) 这个东西就要和原图独立了,于是 \(u\) 就是割点,\(u,v\) 及栈中在 \(v\) 之后的点组成了一个点双。
但是这里要注意我们要在 for 循环里处理点双,因为点双之间并不是独立的,它们可能公用一个且仅公用一个割点(点双的定义)。因此这里处理各个点双出栈时也是只能出到 \(v\),因为我们还没有处理完 \(u\) 有关的全部点双。
这里我们认为两个点中间连一条边是两个点双,一个点或者一个点自己给了自己很多自环也算一个点。
注意在实现时写好特判就能过。
code
Show me the code
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m;
const int N=5e5+5;
const int M=2e6+5;
struct e{
int u;int v;int w;int nxt;
}edge[M*2];
int _head[N];
int cnt=-1;
void add(int u,int v,int w){
cnt++;
edge[cnt].u=u;edge[cnt].v=v;edge[cnt].w=w;
edge[cnt].nxt=_head[u];
_head[u]=cnt;
}
int dfn[N],low[N],vis[N];
bool cutpoint[N];
stack<int> s;
int id=0;
int vdcc=0;
vector<int> dcc[N];
int clr[N];
void tarjan(int u,int fa){
dfn[u]=low[u]=++id;
s.push(u);vis[u]=1;
int svdcc=0;
if(clr[u]==0||clr[u]==1){// 如果是自环或者独立点
vdcc++;dcc[vdcc].push_back(u);
s.pop();vis[u]=0;
return;
}
for(int i=_head[u];i!=-1;i=edge[i].nxt){
int v=edge[i].v;
if(i==(fa^1))continue;
if(!dfn[v]){
tarjan(v,i);svdcc++;
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
cutpoint[u]=1;vdcc++;
dcc[vdcc].push_back(u);
int lst=0;
while(lst!=v){// 这里只能扔到 v
vis[s.top()]=0;
dcc[vdcc].push_back(s.top());
lst=s.top();
s.pop();
}
}
}
else low[u]=min(low[u],dfn[v]);
}
}
int main(){
memset(_head,-1,sizeof _head);
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
u=rd;v=rd;
if(u==v&&clr[u]!=-1){clr[u]=1;}// 这两行判是否是自环,独立点
else if(u!=v){clr[u]=-1;clr[v]=-1;}
add(u,v,1);
add(v,u,1);
}
for(int i=1;i<=n;i++){// 可能不连通
if(!dfn[i])tarjan(i,-1);
}
cout<<vdcc<<'\n';
for(int i=1;i<=vdcc;i++){
cout<<dcc[i].size()<<' ';
for(int j=0;j<dcc[i].size();j++)cout<<dcc[i][j]<<' ';
cout<<'\n';
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号