单调队列与单调栈

前言

经典永流传：“如果一个选手比你小还比你强，你就可以退役了。”

1. 单调队列

1.1 用处

单调队列是一种线性数据结构，可以在 \(O(n)\) 的时间复杂度内求解出一个区间中每一个长度为 \(m\) 的子区间的最值。
虽然其只能维护静态的区间最值，但对比 ST 表和线段树，单调队列的时间复杂度更为优秀。

1.2 原理

顾名思义，单调队列维护一个内部数据为单调的队列。对于一个新数据，采用合适的方式进行出队和入队操作，让每一个区间的最大、最小值就是队列的头或尾。
与一般队列不一样的是，单调队列是一个双向队列，也就是可以在队列的头或尾进行出队入队操作。实现时可以使用数组模拟，也可以使用 C++ STL 中封装好的 deque 容器进行实现，本文均会介绍两种实现。
特别的一点是，单调队列中存储的值是原数组中的下标，因为下标可以确定一个数，但一个数不一定可以确定一个下标。

1.3 实现

例题：

洛谷 P1886 滑动窗口 /【模板】单调队列
有一个长为 \(n\) 的序列 \(a\)，以及一个大小为 \(k\) 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。
例如，对于序列 \([1,3,-1,-3,5,3,6,7]\) 以及 \(k = 3\)，有如下过程：

\[\def\arraystretch{1.2} \begin{array}{|c|c|c|}\hline \textsf{窗口位置} & \textsf{最小值} & \textsf{最大值} \\ \hline \verb![1 3 -1] -3 5 3 6 7 ! & -1 & 3 \\ \hline \verb! 1 [3 -1 -3] 5 3 6 7 ! & -3 & 3 \\ \hline \verb! 1 3 [-1 -3 5] 3 6 7 ! & -3 & 5 \\ \hline \verb! 1 3 -1 [-3 5 3] 6 7 ! & -3 & 5 \\ \hline \verb! 1 3 -1 -3 [5 3 6] 7 ! & 3 & 6 \\ \hline \verb! 1 3 -1 -3 5 [3 6 7]! & 3 & 7 \\ \hline \end{array} \]

这是单调队列的模板题，我们先考虑最大值。
在用单调队列解决问题时，我们要考虑三个问题：

• 这个单调队列是单调递增还是单调递减的？（从队头到队尾）
• 什么时候入队或者出队，头还是尾？
• 答案在哪里？

由于我们习惯让新数据从队尾进入，因此我们希望队头是这个区间的最大值。
也就是说，整个单调队列中的数据是单调递减的。
那么对于一个新数据，怎样入队出队呢？
显然，如果一个后进来的数（这里指区间滑动将这个数包括进去）比前面进来的所有的数都要大，那么前面的所有数不可能再成为这个区间的最大值了（名言来源），因此要让队尾的数全部弹出，直到队空，这是把这个数压入。
如果在弹出队尾的过程中发现队尾比这个数大了，那么这个数可能会因为前面的数不再被滑动窗口包括从而成为这个区间的最大值，所以此时不应再弹出队尾，直接把这个数压到队尾。
由入队过程可以看出，单调队列从队头到队尾的数据进入单调队列的时间是递减的（虽然它们在原数组中不一定连续）。
不过还要注意，如果滑动窗口不再将队列中的某些元素包括了，这时要弹出这些元素。
那么如何判断滑动窗口没有包括的元素呢？
事实上，这样的元素只可能是队头元素。我们分类讨论证明：

• 如果滑动窗口不再包括的这个元素是原来的最大值，那么它就在队头，直接弹出队头即可。
• 如果滑动窗口不再包括的这个元素不是原来的最大值，这证明它在被滑动窗口不在包括前就会被之后进来的比它更大的元素从队尾删去，我们不必再考虑这个元素了。

而判断队头出界的方法也很简单，如果滑动窗口尾部的元素下标减去此元素的下标加一大于滑动窗口的大小，就可以判定它出界了。
于是可以写出求解每个窗口内最大值的代码：
手写队列版：

ll q[(int)1e6+6];
··· 
int h=0,t=-1;//队列的头尾下标 
for(int i=1;i<=n;i++){
	//先判断队头元素是否不再被包括 
	if(h<=t&&i-q[h]+1>k){
	//  ^ 不要忘记判断队列非空！！ 
		//如果是，将队头弹出，也就是头坐标增加1 
		h++;	
	}
	//对一个新元素进行入队和出队操作 
	while(h<=t&&a[q[t]]<=a[i]){
	//     ^ 不要忘记判断队列非空！！	
		//如果尾部元素小于当前元素，直接弹出尾部元素 
		t--;
	}
	//将当前元素压入队尾 
	q[++t]=i;
	
	if(i>=k){//如果已经处理完了k个元素（滑动窗口包括了k个元素，单调队列中不一定有 k 个元素）
		//队头就是最大值，即答案 
		cout<<a[q[h]]<<' ';
	}
}

STL & 压行版：
这里简单介绍 deque 封装的一些函数：

• size() 队列大小，\(0\) 代表队空。
• front() 获取队头元素。
• back() 获取队尾元素。
• pop_front() 弹出队头元素。
• pop_back() 弹出队尾元素。
• push_back() 在队尾插入元素。
• push_front() 在队头插入元素（实现单调队列并不需要使用）。

deque<int> q;
for(int i=1;i<=n;i++){
	if(q.size()&&q.front()<i-k+1)q.pop_front();
	while(q.size()&&a[q.back()]<=a[i])q.pop_back();
	q.push_back(i);
	if(i>=k)cout<<a[q.front()]<<'\n';
}

对于最小值的求解，我们照葫芦画瓢即可：
如果队尾元素大于当前元素，则队尾元素没有用处，直接弹出，直到队尾小于当前元素或队空。
之后直接压入此元素。
在这之前判断队头元素有没有出界，如果出界直接删去。
之后判断一下窗口有没有包括到足够的元素，直接输出。
手写队列版：

int h=0;t=-1;
for(int i=1;i<=n;i++){
	//队列非空的情况下队头出界，直接删去 
	if(h<=t&&i-q[h]+1>k)h++;
	//如果队尾比当前大，直接删去 
	while(h<=t&&a[q[t]]>=a[i])t--;
	//压入当前元素 
	q[++t]=i;
	//包括了足够的数据，可以输出 
	if(i>=k)cout<<a[q[h]]<<' ';
}

STL 版：

deque<int> q;
for(int i=1;i<=n;i++){
	if(q.size()&&i-q.front()+1>k)h++;
	while(q.size()&&a[q.back()]>=a[i])t--;
	q.push_back(i);
	if(i>=k)cout<<a[q.front()]<<' ';
}

1.4 例题

• 洛谷 P2251 质量检测
• *洛谷搬运 P2698 [USACO12MAR] Flowerpot S
• 洛谷 P1440 求m区间内的最小值
• 洛谷 P2032 扫描

2. 单调栈

2.1 用处

单调栈也是一种线性数据结构，可以在 \(O(n)\) 的时间复杂度内求解出一个数组中往左或往右第一个比自己大、小、不大于、不小于的元素的下标。
利用这样的特性，可以求解出诸如 “满足题意的最大矩形面积” 一类的题目。

2.2 原理

单调栈同单调队列一样维护着一个内部元素有单调性的栈，通过对栈顶元素的压入弹出来进行求解。
单调栈同单调队列一样存储的是数组中元素的下标。

2.3 实现

例题 1：

洛谷 P5788 【模板】单调栈
给出项数为 \(n\) 的整数数列 \(a_{1 \dots n}\)。
定义函数 \(f(i)\) 代表数列中第 \(i\) 个元素之后第一个大于 \(a_i\) 的元素的下标，即 \(f(i)=\min_{i<j\leq n, a_j > a_i} \{j\}\)。若不存在，则 \(f(i)=0\)。
试求出 \(f(1\dots n)\)。

简单来说，就是求出这个数列中所有数右侧第一个比自己大的数的位置。
使用单调栈解决问题时要考虑以下方面：

• 怎样的顺序遍历数组？
• 内部元素单调递增还是单调递减？
• 何时入栈，出栈？
• 答案在哪里？

回看题目，由于栈只能从栈顶访问元素，因此我们让答案在栈顶。
又因为题目要求出右边第一个大于的数，因此我们从右往左遍历数列。
现在考虑遍历到的当前元素：
如果当前元素小于栈顶元素，那么右边第一个大于的数就是栈顶元素，直接记录答案，并把自己压入栈（因为后面的数有可能比自己小，这时答案就是自己）。
于是根据这一条压栈规则不难发现，这个题目中的单调栈是单调递增的（从栈顶到栈底来看）。
如果当前元素大于栈顶元素，也就是说栈顶元素并不是答案，由于单调栈内部元素单调递增，所以我们要弹出栈顶元素，直到栈顶元素大于当前元素或者栈空。
如果栈空了，意味着右边没有一个数比它大，即答案为 \(0\)。
如果栈不空，直接记录答案即可。
之后我们把这个元素也压入栈顶。
那么如果当前元素等于栈顶元素呢？这时我们要仔细读题，题目中要求右边第一个大于的数的位置，因此栈顶元素等于当前元素的情况也是不符合题意的，栈顶元素也要被弹出。
如果题目要求解 “右侧第一个不比自己小的数的位置” ，这时当前元素等于栈顶元素的情况是符合题意的，不应继续弹出。

单调栈的栈也可以自己实现，但是由于比赛中一般开启 \(O2\) 优化，这时 STL 容器时间复杂度并不慢，所以以下代码均使用 STL 的 stack 容器实现。
示例代码如下：

const int N=3e6;
ll a[N];
ll ans[N];// 此数组记录答案 
int main(){

	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		a[i]=rd;
	}
	stack<ll> s;
	for(int i=n;i>=1;i--){//从右往左遍历数组 
		if(i==n){//最后一个数的右边没有数，答案必然是 0，做一下特判 
			ans[n]=0;
			//不要忘了将其压入栈 
			s.push(i);
			continue;
		}
		while(s.size()&&a[i]>=a[s.top()])s.pop();//大于等于栈顶，直接弹出 
		if(s.size()==0){//如果栈空了 
			ans[i]=0;//右边没有一个数比自己大，保存答案 
			s.push(i);//压入栈 
		}
		else{
			ans[i]=s.top();//答案是栈顶 
			s.push(i);//压入栈 
		}
	}
	for(int i=1;i<=n;i++){//输出即可 
		cout<<ans[i]<<' ';
	}

	return 0;
}

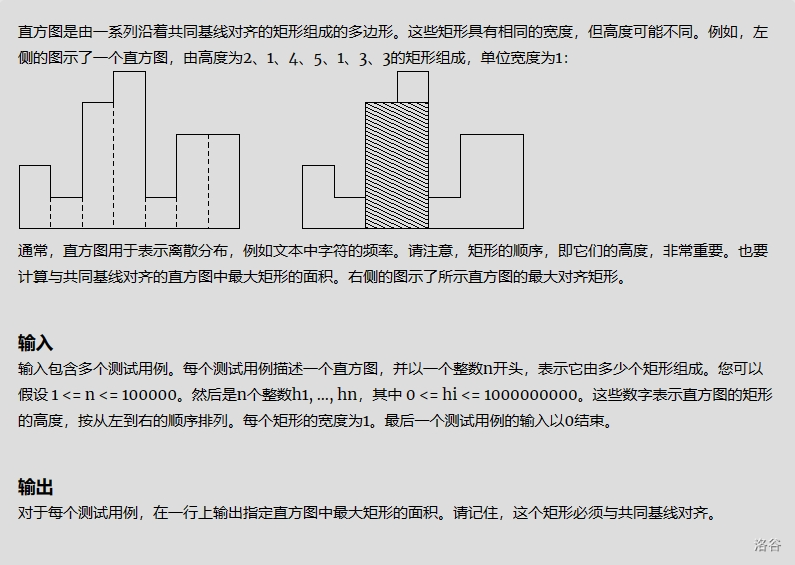
例题 2：

杭电OJ - 1506 直方图中最大的矩形

简单来说，就是在图形中找到面积最大的矩形。
首先面积最大的矩形肯定有一个性质：组成这个矩形的长条至少有一个的纵向高度等于矩形的纵向高度。
原因很简单，如果组成这个矩形的长条的纵向高度均小于矩形的纵向高度，那么这个矩形的纵向高度还能增加，也就是说，这个矩形不是面积最大的矩形。
那么我们得到一个思路：不断枚举每个长条，以这个长条的纵向高度为矩形的纵向高度生成尽可能大的矩形，在所有矩形中取最大值既是答案。
问题来了，怎样确定矩形的长和宽呢？
也就是要求解出：这个长条向左和向右第一个小于这个矩形纵向高度的位置。
这不正是我们单调栈可以解决的事情吗？

• 怎样的顺序遍历数组？
  因为我们要分别求解左边和右边的第一个小于的值，因此左右都要跑一遍。
• 内部元素单调递增还是单调递减？
  显然是单调递减的，因为我们在每次寻找得到答案是都要把自己压入栈，而此时栈顶是小于自己的。
• 何时入栈，出栈？
  如果栈顶元素大于等于自己则让栈顶出栈，当不满足时记录答案，并把自己压入栈。
• 答案在哪里？
  明显在栈顶。

求解出每一个元素左边和右边第一个大于自己的元素的位置后，枚举每一个数，构造矩形，取面积的最大值即可。
示例代码如下：

const int N=1e5+5;
ll h[N];
ll lmin[N],rmin[N];
ll n;
ll matrix(){
	stack<int> s;
	//第一次循环找左边第一个小于自己的数 
	for(int i=1;i<=n;i++){
		if(i==1){
			lmin[i]=i;//第一个数最左边只能到自己 
			s.push(i);//别忘了压入 
			continue;
		}
		while(s.size()&&h[i]<=h[s.top()]){
			s.pop();//栈顶元素大于自己，不符题意，弹出	
		}
		if(s.empty()){
			//如果栈空，证明左边没有一个数比自己小，矩形可以直接延申到数组开头 
			lmin[i]=1;
			s.push(i);
		}
		else{
			//这里要特别注意：  
			//由于单调栈的栈顶一定是第一个小于自己的位置，但是题目中要求的矩形是不能延申到这个比自己小的地方的
			//因此这里的答案应保存为第一个比自己小的位置加一的位置 
			lmin[i]=s.top()+1;
			s.push(i);
		}		
	}
	while(s.size())s.pop();//清空栈准备开始第二次求解
	//第二次求解右边第一个大于自己的位置，倒着遍历数组
	//注意的事项如同上文 
	for(int i=n;i>=1;i--){
		if(i==n){
			rmin[i]=i;
			s.push(i);
			continue;
		}
		while(s.size()&&h[i]<=h[s.top()])s.pop();
		if(s.empty()){
			rmin[i]=n;
			s.push(i);
		}
		else{
			rmin[i]=s.top()-1;
			s.push(i);
		}		
	}
	ll maxs=0;
	for(int i=1;i<=n;i++){
		//注意区间长条个数的计算 
		maxs=max(maxs,h[i]*(rmin[i]-lmin[i]+1));
	}
	
	return maxs;
}
int main(){

	while(1){
		cin>>n;
		if(n==0)break;
		fill(h+1,h+1+n,0);
		fill(lmin+1,lmin+1+n,0);
		fill(rmin+1,rmin+1+n,0);
		for(int i=1;i<=n;i++){
			h[i]=rd;
		}
		cout<<matrix()<<'\n';
	}

	return 0;
}

例题 3：

洛谷 P4147 玉蟾宫
题意简述：找一块矩形土地，要求这片土地都标着 'F' 并且面积最大。

初见这个题好像很不可做：题目中的子矩形十分多，判断每一个格子都是 'F' 时间复杂度十分高，单调栈怎样解决这个问题呢？
我们把每一行（或列，以下用列举例）都看成例题二中的直方图的一条。
之后，如果上一行也是 'F'，我们就把对应列的条的高度的高度加一。
如果上一行不是 'F'，那么把对应的条的高度设为 \(1\)。
如果这一行是 'R'，把对应列的条的高度设为 \(0\)。
在每一行加入后都对这样的直方图进行求解最大矩形面积，求解出来的面积的最大值就是答案。
这样做的原因是：每次新加入一行，这一行的加入并不会使这个图中的满足题意的矩形的面积更劣。
示例代码如下：

ll cmap[1005][1005];
ll a[100005];
ll lp[100005];
ll rp[100005];
int n,m;
ll maxm(){
	stack<int> s;
	//注意这里的循环次数是 m 不是 n 
	for(int i=1;i<=m;i++){
		if(i==1){
			lp[i]=1;
			s.push(i);
			continue;
		}
		while(s.size()&&a[s.top()]>=a[i])s.pop();
		if(s.empty()){
			lp[i]=1;
			s.push(i);
			continue;
		}
		lp[i]=s.top()+1;
		s.push(i);
	}
	while(s.size())s.pop();
	for(int i=m;i>=1;i--){
		if(i==m){
			rp[i]=m;
			s.push(i);
			continue;
		}
		while(s.size()&&a[s.top()]>=a[i])s.pop();
		if(s.empty()){
			rp[i]=m;
			s.push(i);
			continue;
		}
		rp[i]=s.top()-1;
		s.push(i);
	}
	ll ans=0;
	for(int i=1;i<=m;i++){
		ans=max(ans,(rp[i]-lp[i]+1)*a[i]);
	}
	return ans;
}
int main(){
	
		cin>>n>>m;
		ll ans=0;
		for(int i=1;i<=n;i++){
			memset(lp,0,sizeof lp);
			memset(rp,0,sizeof rp);
			//多测不清空，____________ 
			for(int j=1;j<=m;j++){//每次新加入一行 
				char c;
				cin>>c;
				cmap[i][j]=c;
				if(i==1){//如果是第一行，直接给高度数组赋值 
					if(c=='R')a[j]=0;//如果是 'R',条的高度为 0 
					else a[j]=1;//反之是 1 
					continue;
				}
				if(c=='R')a[j]=0;//如果不是第一行且这一行是 'R' ,条的高度为 0 
				else a[j]+=1;//反之将条的高度加一	
			}
			ans=max(ans,maxm());//调用求解直方图最大矩形面积的函数求解答案 
		}
		cout<<ans*3;//输出即可 

	return 0;
}

2.4 例题：

• 洛谷搬运 P2866 [USACO06NOV] Bad Hair Day S
• 杭电OJ - 6957 最大子矩阵

---

迁移自洛谷