【好题选讲】图论中超级源点的应用

前言

图论题中有某些奇怪的条件？试着把他们扔给超级源点！

超级源点是什么

超级源点通常是人造的 \(0\) 号节点。此节点一般与图中所有节点都有连边。
这个节点的加入通常会改变图的连通性，最短路、最小生成树的值，可能会对解题有所帮助。

在求解全源最短路的 Johnson 算法中就应用了超级源点，见这里。

题目示例 1

题意简述

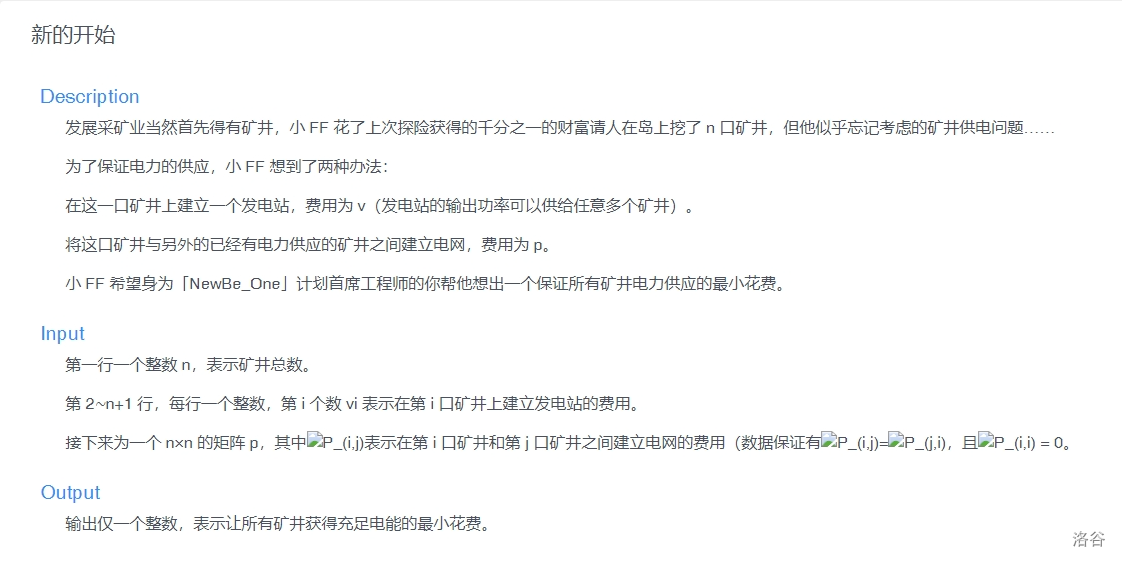
海岛上有些矿井，现在矿井需要供电。有两种供电方式：

• 在矿井头上建一个发电站给矿井供电，只能给自己供电。每一个矿井建发电站的费用不同，在输入中给出。
• 从已经供电的矿井处接电线，矿井之间连电线的费用在输入中给出。

求出将所有矿井都供电所花费的最小费用。

解题思路

从题目描述中就可以猜出题目考察最小生成树。
问题来了，这个题目中允许自己给自己供电，又允许从别的矿井中接入电力，怎样选择呢？
一种贪心的思路是：首先求出整个图的最小生成树的花费，之后在所有节点中选择建造发点站费用最少的，将两者的花费相加即是答案。
但是这样的思路是不对的：如果连接电线花费很高，但所有的矿井自己造发电站都不需要花费，那么我们的思路就会求出错误的答案。
这时我们考虑构建一个超级源点，源点向图中每一个点（也就是每一个矿井）连接一条边，边权为每一个矿井自己造发电厂的费用。
之后，在这个图中求出的最小生成树的权值就是答案。
为什么要这样设置呢？
由于边权的设置，一个点在最小生成树中与超级源点相连，意味着这个矿井自己建发电站。
因为求解的是生成树，所以必须有一条连接超级源点和图中任意节点的边被选中。
这代表这所有矿井中必须有一个建造发电站。正好符合了题目要求。
同时，在生成树中，如果有另外的点也连接了超级源点，这意味着这个矿井不从其它矿井接入电力，而是自己建发电站。
而因为是最小生成树，所以保证了任意点自己建发电站或接电线所花费的总和是最小的。
于是，在这个图上跑出的最小生成树就完美的考虑了所有情况，问题被成功解决。
示例代码如下：
在云剪贴板。

题目示例 2

题意简述

给一个有向图，可以从多个起点出发，到达一个终点，问最短路，没有则输出 -1。

解题思路

一个很容易想到的方法是对每一个起点跑一边 Dijstra，对每一次跑出的结果去最小值即可。
但是这样的方法是 \(O(nm\log m)\) 的，其中 \(m\) 为边数，\(n\) 为起点数，极易超时。
这时我们应用超级源点的思想，如下图：

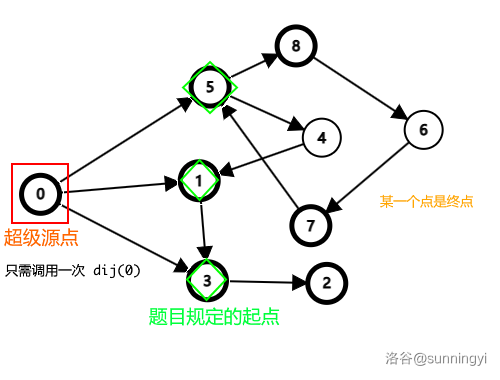
在上图中，我们建立一个超级源点，向每个起点连一条有向边，边权为 \(0\)。

这样，我们仅需对超级源点跑一遍单源最短路即可求出最短距离。
还有一种解法是建反边，这一种更为常用，有时可以更灵活的解决问题。

迁移自洛谷