树上最近公共祖先，LCA

前言

初识倍增思想。

1. 定义

两个节点的最近公共祖先（LCA），就是这两个点的公共祖先里面，离根最远的那个。

2. 求法

朴素求

不断顺着树边往上走，如果走到重合了就是它们的最近公共祖先。
但是，两点之间可能有深度差距，这导致两点在同时向上走的过程中可能会错过。
因此，无论是朴素算法还是更快更常用的倍增算法都需要首先将两点的深度调至相等，也就是先让一个深度更深的点往上跳，另一个不跳。
不过，朴素算法的平均时间复杂度为 \(O(n)\)，其中 \(n\) 为树的节点个数。这显然使我们不能接受的。

倍增法求

应用倍增思想，可以把单次的查询大大优化到 \(O(\log n)\)。
建立一个数组 \(fa_{i,j}\) 表示节点 \(i\) 向上走 \(2^j\) 可以到达的节点编号。
则我们在预处理每一个节点的深度时也可以预处理出 \(fa\) 的值。
为什么要这样设置这个数组呢？
我们考虑任意两个点，假设两个点的深度相等，一起向上走 \(y\) 歩可以到达两个点的 LCA。
我们将 \(y\) 二进制拆分，也就是说 \(y\) 可以写成一些 \(2^j\) 的和，即 \(y\) 的二进制那一位是 \(1\) 的地方，而且 \(j\) 的每一种值仅会出现一次。
这样，我们仅需使用一个 for 循环从大到小枚举 \(j\)，使用 \(fa\) 数组向上跳转即可。
但是在我们没有求出 LCA 之前并不知道 \(y\) 的值，怎样知道 \(y\) 的二进制哪一位是 \(1\) 呢？
其实，在从大到小枚举的过程中，如果 \(y\) 这一位不是 \(1\)，在已经跳转的基础上在跳 \(j\) 歩一定会跳到这两点的公共祖先上。
原因是：一个二进制数第 \(j\) 位是 \(1\) 后面全是 \(0\) 一定比第 \(j\) 位是 \(0\) 后面全是 \(1\) 要大，同样也比后面不全是 \(1\) 要大。
因此，如果我们在 \(y\) 二进制是 \(0\) 的地方跳了 \(2^j\) 歩，此时累计跳的步数就已经比 \(y\) 要大了（这也是从大到小枚举 \(j\) 的原因）。也就会跳到它们的 LCA 还往上的部分，即它们的公共祖先。
因此，我们应在跳转后两点不会碰到公共祖先的情况下进行跳转，但因为这样也跳不到 LCA，因此在循环结束后还要往上再跳一步才是它们的 LCA。
将两点调整至同一高度的过程和这样类似，如果跳多了就会跳到比另一个节点更浅的位置，在循环枚举 \(j\) 的时候加以判断就好了。

预处理深度和 fa 数组的过程通常用 DFS 或 BFS 实现。fa 数组的状态转移方程如下：

\[fa_{i,j}=fa_{fa_{i,j-1},j-1} \]

很好理解：点 \(i\) 向上跳 \(2^j\) 歩，其实就是 \(i\) 跳 \(2^{j-1}\) 歩到达的点在往上跳 \(2^{j-1}\) 歩，向上跳 \(1\) 歩即 \(fa_{i,0}\) 的值就是其父节点。
为了防止 \(2^j\) 的值过大以至于让某些点跳到奇怪的地方，一般设置一个 \(0\) 号节点为“哨兵”，让所有跳出树的 fa 都跳到 \(0\) 号哨兵上。
示例代码如下，其中预处理部分使用 BFS 实现：

Show me the code

const int N=5e5+10;
const int lgr=31;//倍增的系数，一般是 log n 的值，取 31 足够 
vector<int> edge[N];
int n,m,r;
int fa[N][lgr+10];//倍增数组 
int dep[N];//深度 
queue<int> q;
void bfs(int root){//预处理 
	memset(dep,0x3f,sizeof dep);//初始化深度为无限大来判断一个点的深度是否被求出 
	fa[root][0]=0;//根节点向上会跳到一个“哨兵” 
	dep[root]=1;//根节点的深度为 1 
	dep[0]=0;//哨兵的深度为 0 
	q.push(root);//压入队列，开始 BFS 
	while(q.size()){
		int u=q.front();
		q.pop();
		for(int i=0;i<edge[u].size();i++){//遍历孩子 
			int v=edge[u][i];
			if(dep[v]>dep[u]+1){//如果深度未被更新 
				dep[v]=dep[u]+1;//更新深度 
				fa[v][0]=u;//孩子向上跳一个是自己 
				q.push(v);//压入队列 
				for(int j=1;j<=lgr;j++){//处理 fa 数组，注意从小到大 
					fa[v][j]=fa[fa[v][j-1]][j-1];
				}
			}
		}
	}
}
int lca(int a,int b){
	if(dep[a]<dep[b]){//如果 a 的深度小于 b，则让 a,b 交换以确保 a 总是深度大的那一个 
		swap(a,b);
	}
	if(a==b)return a;//如果两点重合，那么 LCA 就是他们自己，直接返回 
	for(int i=lgr;i>=0;i--){//处理 a 点让他们的深度相同 
		if(dep[fa[a][i]]>=dep[b]){//在更深或者深度相同的情况下才允许跳转 
			a=fa[a][i];
		}
	}
	if(a==b)return a;//如果跳转后两点重合 ，那么 LCA 就是他们自己，直接返回 
	for(int i=lgr;i>=0;i--){//求解 LCA 
		if(fa[a][i]!=fa[b][i]){//在跳不到公共祖先的情况下才允许跳转 
			a=fa[a][i];
			b=fa[b][i];
		}
	}
	return fa[a][0];//注意要再往上跳一个！！！ 
}
int main(){
	
	n=rd;
	m=rd;
	r=rd;
	for(int i=1;i<=n-1;i++){
		int u=rd,v=rd;
		edge[u].push_back(v);
		edge[v].push_back(u);
	}
	bfs(r);//不要忘了预处理！！！ 
	for(int i=1;i<=m;i++){
		int a=rd,b=rd;
		cout<<lca(a,b)<<'\n';
	}
	
	return 0;
}

括号序列 + ST 表

挺重要的一个东西，用到了 DFN 序的一些小知识，回顾一下吧。

从根出发向下进行 DFS，过程中给每个点一个编号，用编号作为下标把点组织起来的序列叫做这个树的 DFN 序。

当然了，只用 DFN 序并不能解决求解 LCA 的问题，我们对它做些加强：

从根出发向下进行 DFS，过程中给每个点一个编号，但是在父亲节点，递归完成一个子树的编号后，我们在给这个点一个编号，这个规则对子树的标号也有效。容易发现的是，如此这般，一个节点可能会有多个编号。若以编号为下标，点为值可得到一个序列。我们把这样的序列叫做括号序列，或者 Euler 序列。

这种序列会对我们求解 LCA 有很大帮助。设想：我们总是在递归完成一个子树后给父节点按上的标签，然后才去进行下一个子树的遍历，显然的，对于一个节点中任意的两个子树，其在括号序列的标号区间中间夹着的一块必定有父亲节点的编号，且父亲节点的是夹着的这个区间中的点的深度最小的。

这样我们有个很好的性质：对于任意两个点 \(u,v\)，令它们在括号序中第一次出现的位置为 \(f(u),f(v)\)，则在括号序列上的区间 \([f(u),f(v)]\) 必定包含且只包含了 \(u,v\) 的最近公共祖先。于是求解 LCA 问题变成了：求解区间 \([f(u),f(v)]\) 上深度最小的节点编号。

这是一个标准的 RMQ 问题，使用 ST 表可以做到 \(O(n\log{n})\) 预处理，\(O(1)\) 常数。常数时间的查询对某些题目很重要。

实现是注意要同时存最小值和取到最小值的点的编号。

code，微压行

Show me the code

#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
  ll x=0,f=1;
  char c=getchar();
  while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
  while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
  return x*f;
}
int n,m,s;
const int N=5e5+1145;
const int lgr=25;
vector<int> edge[N];
int cnt=0;
int num[N*3],fp[N];
void dfs(int u,int fa){
  cnt++;
  if(fp[u]==0)fp[u]=cnt;
  num[cnt]=u;
  for(int i=0;i<edge[u].size();i++){
    int v=edge[u][i];
    if(v==fa)continue;
    dfs(v,u);cnt++;
    num[cnt]=u;
  }
  return ;
}
int dep[N];
void bfs(int r){
  memset(dep,0x3f,sizeof dep);
  queue<int> q;
  q.push(r);
  dep[r]=0;
  while(q.size()){
    int u=q.front();
    q.pop();
    for(int i=0;i<edge[u].size();i++){
      int v=edge[u][i];
      if(dep[v]>dep[u]+1){
        dep[v]=dep[u]+1;
        q.push(v);
      }
    }
  }
  return;
}
int a[N*3];
pair<int,int> f[N*3][30];
int lg[N*3];
int main(){
  
  cin>>n>>m>>s;
  for(int i=1;i<n;i++){
    int u,v;
    u=rd;v=rd;
    edge[u].push_back(v);
    edge[v].push_back(u);
  }
  dfs(s,-1);
  bfs(s);
  lg[2]=1;lg[1]=lg[0]=0;
  for(int i=1;i<=cnt;i++){
    a[i]=dep[num[i]];
    f[i][0].first=dep[num[i]];
    f[i][0].second=num[i];
    if(i<3)continue;
    lg[i]=lg[i/2]+1;
  }
  for(int j=1;j<lgr;j++){
    for(int i=1;i+(1<<j)-1<=cnt;i++){
      if(f[i][j-1].first<f[i+(1<<(j-1))][j-1].first){
        f[i][j].first=f[i][j-1].first;
        f[i][j].second=f[i][j-1].second;
      }
      else{
        f[i][j].first=f[i+(1<<(j-1))][j-1].first;
        f[i][j].second=f[i+(1<<(j-1))][j-1].second;
      }
    }
  }
  for(int i=1;i<=m;i++){
    int u,v;
    u=rd;v=rd;
    if(u==v){
      cout<<u<<'\n';
      continue;
    }
    int u1=fp[u],v1=fp[v];
    if(u1>v1)swap(u1,v1);//区间不能左大于右 
    int s=lg[v1-u1+1],int ans;
    if(f[u1][s].first<f[v1-(1<<s)+1][s].first){
      cout<<f[u1][s].second<<'\n';
      continue;
    }
    else{
      cout<<f[v1-(1<<s)+1][s].second<<'\n';
      continue;
    }
  }
  
  return 0;
}

Tarjan 离线

这东西不怎么常用，说下原理吧。

Tarjan 离线 LCA 的时间复杂度为 \(O(n)\) 预处理，\(O(1)\) 查询。但作为代价，你必须知道有哪些节点的 LCA 要被查询。换句话说，你不可以当需要用到某对节点的 LCA 时再去查询。

Tarjan 依然从根开始使用 DFS 对树进行处理，利用并查集辅助记录当前 DFS 到的根节点情况。

具体的，DFS 时遵循以下步骤：

将该节点标记为已访问。
递归向下 DFS 各儿子。
一个儿子 \(v\) 递归完成后，令 \(fa(v)=u\)。
所有儿子查询完成后，遍历与自己有查询关系的点，如果该节点已被访问，则两个点的 LCA 为 \(find(u,v)\)。

原理应该是显然的，模拟一遍过程就明白了。

你说得对，但是我是在没想懂怎么维护这个 有查询关系的点，这可能就是这东西不常用的原因。

没有 code 啦~

重链剖分

重链剖分的性质天然适合维护 LCA。

详见这个文章中的题目 - LCA 模板部分。

3. LCA 的用处

求解树上路径长

我们知道，树上任意两点之间仅有一条简单路径，如何快速求解这样的路径的长度呢？
我们可以利用前缀和的思想，如下图：

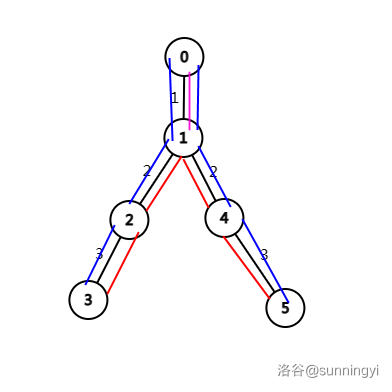
其中，从节点 \(3\) 到节点 \(5\) 的路径（红色路径）长度为节点 \(3\) 到根节点（左侧蓝色路径）与节点 \(5\) 到根节点（右侧蓝色路径）之和减去节点 \(3\) 与节点 \(5\) 的 LCA，即 \(1\) 号节点到根节点路径的两倍。
而每一个节点到根节点的距离也可以在 BFS 时求解出。
这样，我们就可以在可以接受的时间复杂度内知道任意两点之间的最短路径了！
例题：
洛谷 P8855
洛谷 P8805

posted @ 2025-02-04 13:18 hm2ns 阅读(67) 评论(0) 收藏举报

刷新页面返回顶部

hm2nsite

不过总有一天，我的心会游过夜晚，游到走累的你的身边