线段树
前言
花了一天浅学线段树,好用!
1. 概述
线段树是一种二叉搜索树,用来处理一些满足结合律的问题(可以用小区间合并求出大区间解的问题)。经典的例子有求区间和,区间积,区间最大公约数,区间最值等问题,且时间复杂度为 \(O(\log n)\) 级别。
2. 实现原理及模板代码分析
线段树,顾名思义就是将原数组存储为一些线段,叠起来像树一样。要使用线段树,我们要先建树。下面的例子实现了线段树的区间加法和区间查询。
2.1 建树
我们知道,对于二叉树,当用数组表示时,它的左儿子的下标是原始下标\(\times 2\),右儿子的下标是原始下标\(\times 2+1\)。于是我们可以用递归的思想建树。
对于表示线段树的数组,我们用结构体实现,如下:
const int MAXN=(int)(1e5+5)*4;
struct segment_tree{
ll v;//这个节点表示的区间的值
ll l;//区间左端点
ll r;//区间右端点
ll lazyt;//一些懒标记
}segtree[MAXN];
注意:对一个数组用线段树维护时线段树数组大小是原数组的4倍
之后,我们实现一个函数 void buildt(int l,int r,int p) 表示用线段树数组下标为 \(p\) 的节点表示原数组中 \(l\) 到 \(r\) 的信息,如下:
inline void buildt(int l,int r,int p){
segtree[p].l=l;//左右端点赋值
segtree[p].r=r;
segtree[p].lazyt=0;//没有懒标记
if(l==r){//当左端点等于右端点时,代表这棵线段树的叶子节点,直接赋值
segtree[p].v=num[l];//不要写成 num[p]
return;//叶子节点已经到底,无需进行其他操作
}
int mid=(l+r)>>1;//取中心点
buildt(l,mid,p*2);//递归建左子树
buildt(mid+1,r,p*2+1);//递归建右子树
segtree[p].v=segtree[p*2].v+segtree[p*2+1].v;
//这个节点(区间)的值由他的左右节点(两个子区间)的值相加而来
}
建树操作即调用 buildt(1,n,1);。
一般地,线段树数组的下标 1 是线段树的根节点。
如图是对一个下标为 \(1\sim 8\) 的数组构建的线段树,叶子节点的懒标记省略:
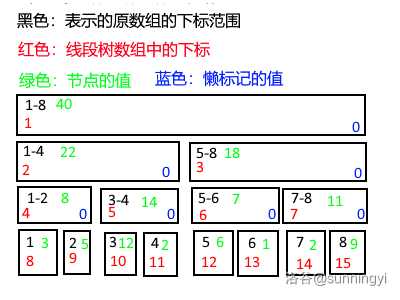
2.2 区间修改
注意到单点修改就是区间修改的特殊形式,于是只实现区间修改即可。
给定一个区间,把区间里的数全都加上k。
我们想到暴力模拟,但是对于 \(q\) 次平均长度是 \(n\) 的操作,时间复杂度是 \(O(nq)\),稍大点便会超时。
但是我们可以把给定的区间分解成一些小区间,在线段树中只修改这些区间的值,这时需要运用到懒标记。
懒标记,就是把这个大区间的修改改信息先不对区间里的每一个节点修改,而是扣下来,存在大区间所代表的节点里,等到需要时一层一层再往儿子节点传即可。
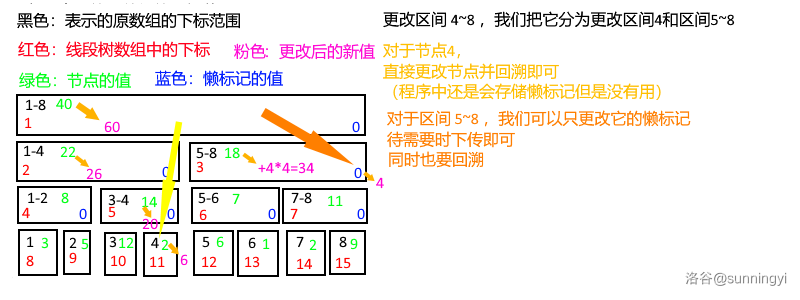
以下图解以 “将区间 \(4\sim 8\) 的值增加 \(4\)” 为例解释了懒标记:
(对于区间 \(5\sim 8\),除了更新懒标记,值也要更新!)
不过,我们发现在修改时也可能会碰到修改的小区间的父区间有懒标记的情况,这时我们也要进行下传。
问题来了,如何拆分区间呢?
当一个节点的区间完全被所求区间包含时,这个节点区间的所有节点都要被更新,此时我们只需更新这个节点的值并更新懒标记。
当一个节点的区间被部分包含时,则向下搜索这个节点左右子区间(两个子节点可能只包含一个,也可能两个全部包含)。
更新完成子节点后,回溯更新父节点的值。
我们发现也可以递归实现。
我们实现一个函数 void add(int k,int l,int r,int p) 表示对区间 \(l,r\) 增加 \(k\),\(p\) 为当前节点下标。
inline void add(int k,int l,int r,int p){
if(l<=segtree[p].l&&segtree[p].r<=r){//此区间完全包含于修改区间
segtree[p].v+=k*(segtree[p].r-segtree[p].l+1);
//新值=以前值+每个节点增加值*节点数量
segtree[p].lazyt+=k;
//更新懒标记
return;//一定要return不然会导致重复计算
}
push_down(p);//对懒标记的下传,见下文
//当左子区间被部分包含
if(l<=segtree[p*2].r){//不要写 l<=segtree[p*2].l
add(k,l,r,p*2);
}
//当右子区间被部分包含
if(segtree[p*2+1].l<=r){//不要写 else if ,不要写 segtree[p*2+1].r<=r
add(k,l,r,p*2+1);
}
segtree[p].v=segtree[p*2].v+segtree[p*2+1].v;//处理完左右子区间后更新此节点的值
return;
}
问题又来了,如何下传懒标记呢?
2.3 懒标记的下传
线段树最灵活的部分,不同种类的线段树实现的方法可能大相径庭
首先,因为加法线段树懒标记表示的是每个叶子节点增加的值,因此下传时要把此节点的懒标记赋值给两个子节点。
其次,懒标记的存在是因为只更新了大区间的值而没有更新小区间的值而产生的,因此在下传时,子节点所代表的区间的值也要一并更新。
最后,因为此节点的懒标记已经下传,所以此节点懒标记的值要归零。
为如下代码:
inline void push_down(int p){
if(segtree[p].lazyt!=0){//有懒标记需要下传时
int k=segtree[p].lazyt;
//下传给左右两子线段
segtree[p*2].lazyt+=k;
segtree[p*2+1].lazyt+=k;
//更新左右两子线段的值 v
int mid=(segtree[p].r+segtree[p].l)>>1;
segtree[p*2].v+=k*(segtree[p*2].r-segtree[p*2].l+1);
segtree[p*2+1].v+=k*(segtree[p*2+1].r-segtree[p*2+1].l+1);
segtree[p].lazyt=0;
}
}
2.4 区间求和
我们在线段树里已经存好了一些区间的和,只要我们把给定的区间分解成一些小区间,在线段树中查找这些区间的值,再合并即可获得答案。
与区间加法同理,当一部分线段树的一部分区间被完全包含于求和的区间时,返回该区间的值。
当一个节点的区间被部分包含时,则向下搜索这个节点左右子区间(两个子节点可能只包含一个,也可能两个全部包含)。之后返回这两个子区间的值。
另外,在查询时也要下传懒标记。
代码实现如下:
inline ll q(int l,int r,int p){
if(l<=segtree[p].l&&segtree[p].r<=r){//完全包含,直接返回此区间的值
return segtree[p].v;
}
if(l>segtree[p].r||r<segtree[p].l)return 0;//没有包含当前区间,直接退出 **一定要写这一部分**
push_down(p);//查询时也要下传懒标记
ll sub=0;//两区间的和
if(l<=segtree[p*2].r){//左区间被部分包含
sub+=q(l,r,p*2);//加入和
}
if(segtree[p*2+1].l<=r){//右区间同理
sub+=q(l,r,p*2+1);
}
return sub;//返回两区间和作为更大的和
}
完整代码如下
这个模板一定要背过,不能写错!
测试样例:
Input:
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
Output:
11
8
20
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int MAXN=(int)(1e5+5)*4;
struct segment_tree{
ll v;
ll l;
ll r;
ll lazyt;
}segtree[MAXN];
int num[(int)1e5+5];
inline void upd(int p){
segtree[p].v=segtree[p*2].v+segtree[p*2+1].v;
}
inline void buildt(int l,int r,int p){
segtree[p].l=l;
segtree[p].r=r;
segtree[p].lazyt=0;
if(l==r){
segtree[p].v=num[l];
return;
}
int mid=(l+r)>>1;
buildt(l,mid,p*2);
buildt(mid+1,r,p*2+1);
upd(p);
}
inline void push_down(int p){
if(segtree[p].lazyt!=0){//有懒标记需要下传时
int k=segtree[p].lazyt;
//下传给左右两子线段
segtree[p*2].lazyt+=k;
segtree[p*2+1].lazyt+=k;
//更新左右两子线段的值 v
int mid=(segtree[p].r+segtree[p].l)>>1;
segtree[p*2].v+=k*(segtree[p*2].r-segtree[p*2].l+1);
segtree[p*2+1].v+=k*(segtree[p*2+1].r-segtree[p*2+1].l+1);
segtree[p].lazyt=0;
}
}
inline void add(int k,int l,int r,int p){
if(l<=segtree[p].l&&segtree[p].r<=r){
segtree[p].v+=k*(segtree[p].r-segtree[p].l+1);
segtree[p].lazyt+=k;
return;
}
push_down(p);
if(l<=segtree[p*2].r){
add(k,l,r,p*2);
}
if(segtree[p*2+1].l<=r){
add(k,l,r,p*2+1);
}
segtree[p].v=segtree[p*2].v+segtree[p*2+1].v;
return;
}
inline ll q(int l,int r,int p){
if(l<=segtree[p].l&&segtree[p].r<=r){//完全包含,直接返回此区间的值
return segtree[p].v;
}
if(l>segtree[p].r||r<segtree[p].l)return 0;//没有包含当前区间,直接退出 **一定要写这一部分**
push_down(p);//查询时也要下传懒标记
ll sub=0;//两区间的和
if(l<=segtree[p*2].r){//左区间被部分包含
sub+=q(l,r,p*2);//加入和
}
if(segtree[p*2+1].l<=r){//右区间同理
sub+=q(l,r,p*2+1);
}
return sub;//返回两区间和作为更大的和
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
num[i]=read();
}
buildt(1,n,1);//DO NOT FORGET THIS
for(int i=1;i<=m;i++){
int op;
op=read();
if(op==1){
int l=read(),r=read(),k=read();
add(k,l,r,1);
}
else{
int l=read(),r=read();
cout<<q(l,r,1)<<'\n';
}
}
return 0;
}
short ver.
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int MAXN=(int)(1e5+5)*4;
struct segment_tree{
ll v;
ll l;
ll r;
ll lazyt;
}t[MAXN];
int num[(int)1e5+5];
inline void upd(int p){
t[p].v=t[p*2].v+t[p*2+1].v;
}
inline void buildt(int l,int r,int p){
t[p].l=l;
t[p].r=r;
t[p].lazyt=0;
if(l==r){
t[p].v=num[l];
return;
}
int mid=(l+r)>>1;
buildt(l,mid,p*2);
buildt(mid+1,r,p*2+1);
upd(p);
}
inline void push_down(int p){
if(t[p].lazyt!=0){//有懒标记需要下传时
int k=t[p].lazyt;
//下传给左右两子线段
t[p*2].lazyt+=k;
t[p*2+1].lazyt+=k;
//更新左右两子线段的值 v
int mid=(t[p].r+t[p].l)>>1;
t[p*2].v+=k*(t[p*2].r-t[p*2].l+1);
t[p*2+1].v+=k*(t[p*2+1].r-t[p*2+1].l+1);
t[p].lazyt=0;
}
}
inline void add(int k,int l,int r,int p){
if(l<=t[p].l&&t[p].r<=r){
t[p].v+=k*(t[p].r-t[p].l+1);
t[p].lazyt+=k;
return;
}
push_down(p);
if(l<=t[p*2].r){
add(k,l,r,p*2);
}
if(t[p*2+1].l<=r){
add(k,l,r,p*2+1);
}
t[p].v=t[p*2].v+t[p*2+1].v;
return;
}
inline ll q(int l,int r,int p){
if(l<=t[p].l&&t[p].r<=r){//完全包含,直接返回此区间的值
return t[p].v;
}
push_down(p);//查询时也要下传懒标记
ll sub=0;//两区间的和
if(l<=t[p*2].r){//左区间被部分包含
sub+=q(l,r,p*2);//加入和
}
if(t[p*2+1].l<=r){//右区间同理
sub+=q(l,r,p*2+1);
}
return sub;//返回两区间和作为更大的和
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
num[i]=read();
}
buildt(1,n,1);//DO NOT FORGET THIS
for(int i=1;i<=m;i++){
int op;
op=read();
if(op==1){
int l=read(),r=read(),k=read();
add(k,l,r,1);
}
else{
int l=read(),r=read();
cout<<q(l,r,1)<<'\n';
}
}
return 0;
}
3. 更多种类的线段树
见 线段树扩展应用(基础)。
迁移自洛谷


 浙公网安备 33010602011771号
浙公网安备 33010602011771号