并查集

前言

看到 NOIp2023 考了才来学
现在才学是不是太菜了?

1. 普通并查集

并查集是一种可以快速合并集合、判断几个元素是否在同一集合内的树形数据结构。
并查集使用一个数组存储每个节点的父节点，因此他的空间复杂度是 \(O(n)\)。

1.1 初始化

为了判断这个节点是否还有父节点，我们在初始化时让每个节点指向自己，即每个节点互相独立，方便以后操作时的判断。

代码实现如下：

for(int i=1;i<=node;i++){
	fa[i]=i//自己指自己
}

1.2 寻找祖先

可以简单理解为顺着父节点数组向上爬的过程，用递归实现。
递归的终点是什么？在递归时，我们一定会找到一个节点的父节点指向自己。这个节点就是我们要找的节点的祖先，直接返回即可。
代码实现如下：

int _find(int _unit){
	if(fa[_unit] == _unit)return _unit;
    //一个节点的父节点指向自己，直接返回即可。

	else return _find(fa[_unit]);//顺着父节点数组向上爬
}

这时我们会发现一个问题，当这个并查集退化成一条链的形式（如下图），每一次查找的平均时间复杂度会变成 \(O(n)\)。如何优化呢？

考虑每一个节点，我们发现，这个节点直接指向祖先 和 指向一个指向祖先的节点 是等价的，所以我们可以将上图中的节点 5,1,2,3 全部指向节点 0（如下图），这样的查找时间复杂度就变成了 \(O(1)\)。

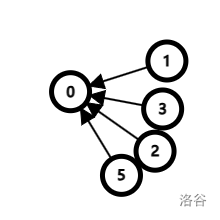
如何代码实现呢？很简单，只需要将传下来的祖先位置依次赋值给每一个归到的节点的父节点数组即可。
代码实现如下：

int _find(int _unit){
	if(fa[_unit]==_unit)return _unit;
    //一个节点的父节点指向自己，直接返回即可。
	fa[_unit]= _find(fa[_unit]);
    //将传下来的祖先位置赋值给归到的节点的父节点数组
	return fa[_unit];
    //接着将祖先位置向下传
}  

或是可以更简洁的写成这样：

int _find(int u){
	return fa[u]==u?u:(fa[u]=_find(fa[u]));
}
/*
	当判断中 fa[u]==u 不成立时
	return 关键字先调用 _find(fa[u]) 得到返回值，之后给 fa[u] 赋值，
	最后返回 fa[u] 的值
*/

“这个节点直接指向祖先和指向一个指向祖先的节点是等价的” 同时体现了集合的无序性。

1.3 判断操作

给两个节点，问它们两个是否属于同一个集合？

原理很简单，只要它们两个有同一个祖先，它们自然属于同一个集合。
怎样算作祖先？根据初始化，节点的父节点指向自己的是祖先。
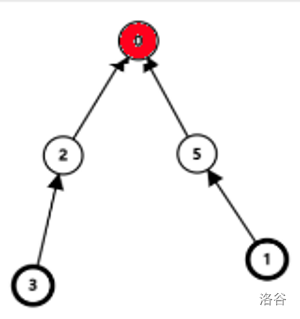
下面的图解解释了“只要它们两个有同一个祖先，它们自然属于同一个集合”。

在图中，要判断加粗的节点3,1是否在同一集合，而它们有一个共同的祖先，即标红的节点0，所以它们在同一集合。

代码实现如下：

int u1,u2;
cin>>u1>>u2;
//要判断的两个节点
int t1=_find(u1)
   ,t2=_find(u2);
//找祖先
if(t1==t2)cout<<"Yes"<<'\n';//祖先相同，在同一集合
else cout<<"No"<<'\n';//反之不在同一集合

1.4 合并操作

给两个节点，将这两个节点所在的集合合并

找到两个节点的两个祖先，把其中一个祖先的父节点设置为另一个祖先即可。
有了前面的铺垫，实现很简单：

int u1,u2;
cin>>u1>>u2;
//要合并的两个节点
int t1=_find(u1),t2=_find(u2);
//找祖先
fa[t1]=t2;
//一个祖先的父节点设置为另一个祖先

综合运用

洛谷 P1551 亲戚

亲戚类问题通常可以用并查集解决。
本题的亲戚关系有这样的特点：如果两个人都与一个人有亲戚关系，那么这两个人也有亲戚关系，且与这两个人有亲戚关系的人全部互相有亲戚关系。
很明显，我们可以用并查集将有关系的人统一的一个集合中去，再进行判断。
代码实现如下：

#include<bits/stdc++.h>
using namespace std;
int fa[(int)1e4+5];
int _find(int _unit){
	if(fa[_unit]==_unit)return _unit;
	fa[_unit]= _find(fa[_unit]);
	return fa[_unit];
}
void merge(int u1,int u2){
	int t1=_find(u1),t2=_find(u2);
	fa[t1]=t2;
}
//上文提及的查找和合并函数 
int main(){
	
	int node,op1,op2;
	cin>>node>>op1>>op2;
	for(int i=1;i<=node;i++){
		fa[i]=i;
	}
	//初始化 
	for(int i=1;i<=op1;i++){
		int u1,u2;
		cin>>u1>>u2;
		merge(u1,u2);
	}
	//合并 
	for(int i=1;i<=op2;i++){
		int u1,u2;
		cin>>u1>>u2;
		int t1=_find(u1)
		   ,t2=_find(u2);
		if(t1==t2)cout<<"Yes"<<'\n';
		else cout<<"No"<<'\n';
	}
	//判断同一集合 

	return 0;
}

2. 可扩展域并查集

---

迁移自洛谷