P3640 [APIO2013] 出题人 做题记录
第一次感觉做题这么累,但也是学到三种最短路(准确来说是四种?)的卡法(还是很亏)。
第一问
首先我们观察一下这个第一问的各个算法以及它的特点:
- Floyd 算法:代码是严格的 \(O(V^3)\),而松弛运动完全没算……
- Bellman–Ford 算法(优化形态):其实就只增加了没有松弛就退出的部分……如果没有负权是 \(O(kE)\)(\(k\) 是小常数,\(E\) 是边数),但如果有负权就是 \(O(VE)\),我们也是从这里下手。为什么?因为负权会让 BF 不断地松弛,从而让优化无用。
- Dijkstra 算法(堆优化版本):越看越奇怪,为什么没有
vis数组?因为这其实是堆优化版本的 SPFA,在负权情况下我们能将其复杂度卡到指数级别。
Task 1
送分,\(V>100\) Floyd 就没救了,但注意询问至少要一个。
点击查看代码
//Just Sayori
#pragma GCC diagnostic ignored "-Wnarrowing"
#pragma GCC diagnostic ignored "-Wsign-compare"
#include <iostream>
#include <cstdio>
#include <algorithm>
#define ll long long
#define rnt register int
#define gr getchar
#define pr putchar
#define N 500005
#define M 1000000007
using namespace std;
inline ll read()
{
int f = 1;
ll x = 0;
char ch = gr();
while (ch < '0' || ch > '9') ch == '-' ? f = -1, ch = gr() : ch = gr();
while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + (ch ^ 48), ch = gr();
return x * f;
}
inline void write(ll x)
{
static int top = 0, sta[39];
if (x < 0) pr('-'), x = -x;
do sta[++top] = x % 10, x /= 10;
while (x);
while (top) pr(sta[top--] ^ 48);
}
int main()
{
write(101),pr(10);
for (rnt i=1;i<=100;i++) write(0),pr(10);
write(1),pr(10),write(0),pr(32),write(1),pr(10);
return 0;
}
Task 2
难度不小,由于要保 Floyd 所以 \(V\) 最大开到 100,然后我们考虑如何卡 BF,其实不难,由于这个代码松弛操作是按编号来的,所以我们考虑倒着让大编号的松弛小编号的。也不要忘记上负权,我们拿一些点组成一条负权链,然后旁边再放一条正权链,0 号点给正权链的所有点连 999999 的边权的边,给负权链的所有点连 -1 的边权的边,然后对于每个点,随机向其他点连一点边,边权不定,然后查询正权链或者负权链最下边的点就可以了。虽然我写的很有问题,但是 T=2222 弥补了这一点。
点击查看代码
//Just Sayori
#pragma GCC diagnostic ignored "-Wnarrowing"
#pragma GCC diagnostic ignored "-Wsign-compare"
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <random>
#define ll long long
#define rnt register int
#define gr getchar
#define pr putchar
#define N 500005
#define M 999999
using namespace std;
inline ll read()
{
int f = 1;
ll x = 0;
char ch = gr();
while (ch < '0' || ch > '9') ch == '-' ? f = -1, ch = gr() : ch = gr();
while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + (ch ^ 48), ch = gr();
return x * f;
}
inline void write(ll x)
{
static int top = 0, sta[39];
if (x < 0) pr('-'), x = -x;
do sta[++top] = x % 10, x /= 10;
while (x);
while (top) pr(sta[top--] ^ 48);
}
int top;
int stack[N][2];
int main()
{
mt19937 rand(time(0));
int n=100,cnt=2;
write(n),pr(10);write(99),pr(32);
for (rnt i=1;i<=50;i++) write(i),pr(32),write(M),pr(32),cnt+=2;
for (rnt i=51;i<=99;i++) write(i),pr(32),write(-1),pr(32),cnt+=2;
pr(10);
for (rnt i=50;i>1;i--)
{
top=0;
stack[++top][0]=i-1,stack[top][1]=rand()%M+1;
for (rnt j=i-2,num=0;j>=1;j--)
if (rand()%2 && num<=8)
stack[++top][0]=j,stack[top][1]=(rand()%M+1),num++;
write(top),pr(32),cnt++;
for (rnt i=1;i<=top;i++) write(stack[i][0]),pr(32),write(stack[i][1]),pr(10),cnt+=2;
}
pr(48),pr(10),cnt+=1;
for (rnt i=99;i>51;i--)
{
top=0;
stack[++top][0]=i-1,stack[top][1]=-(rand()%M+1);
for (rnt j=i-2,num=0;j>=1;j--)
if (rand()%2 && num<=9)
stack[++top][0]=j,stack[top][1]=-(rand()%M+1),num++;
write(top),pr(32),cnt++;
for (rnt i=1;i<=top;i++) write(stack[i][0]),pr(32),write(stack[i][1]),pr(10),cnt+=2;
}
pr(48),pr(10),cnt+=1;
write(10),pr(10),cnt+=1;
for (rnt i=1;i<=10;i++) write(0),pr(32),write(50),pr(10),cnt+=2;
return 0;
}
Task 3
你会发现和 Task 1 一模一样,略。
Task 4
我们知道堆优化的 SPFA 遇到负权会出现指数级别的复杂度,怎么做呢?
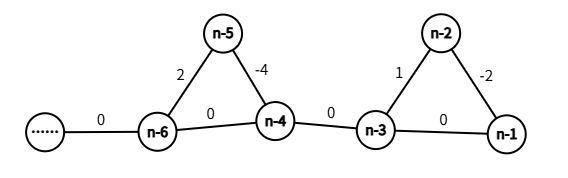
如图,我们先走到 \(n-1\),然后返回到 \(n-3\) 后又去到 \(n-2\) 发现从 \(n-2\) 走更优,然后又走到 \(n-1\),返回到 \(n-6\),然后走 \(n-5\)……然后走到 \(n-1\),然后又从 \(n-2\) 走到 \(n-1\),发现这是指数级的上升,所以取个 \(n=33\) 就可以卡掉了。
点击查看代码
//Just Sayori
#pragma GCC diagnostic ignored "-Wnarrowing"
#pragma GCC diagnostic ignored "-Wsign-compare"
#include <iostream>
#include <cstdio>
#include <algorithm>
#define ll long long
#define rnt register int
#define gr getchar
#define pr putchar
#define N 500005
#define M 1000000007
using namespace std;
inline ll read()
{
int f = 1;
ll x = 0;
char ch = gr();
while (ch < '0' || ch > '9') ch == '-' ? f = -1, ch = gr() : ch = gr();
while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + (ch ^ 48), ch = gr();
return x * f;
}
inline void write(ll x)
{
static int top = 0, sta[39];
if (x < 0) pr('-'), x = -x;
do sta[++top] = x % 10, x /= 10;
while (x);
while (top) pr(sta[top--] ^ 48);
}
int p2[17];
int main()
{
int n=33;
write(n),pr(10),p2[0]=1;
for (rnt i=1;i<=16;i++) p2[i]=p2[i-1]*2;
for (rnt i=0,p=(n-1)/2;i<n-1;i++)
if (i&1)
write(1),pr(32),write(i+1),pr(32),write(-p2[p--]),pr(10);
else
write(2),pr(32),write(i+1),pr(32),write(p2[p-1]),pr(32),write(i+2),pr(32),write(0),pr(10);
write(0),pr(10);//注意最后一个点不连边
write(10),pr(10);
for (rnt i=1;i<=10;i++) write(0),pr(32),write(n-1),pr(10);
return 0;
}
Task 5
照着 Task 2,把 \(n\) 调成 300,然后发现 1016 比 2222 小了一倍多,把随机连边删了还不够,最后让 0 号点向前 50 个点连边才勉强卡够。代码太屎山了,懒得改了:(
点击查看代码
//Just Sayori
#pragma GCC diagnostic ignored "-Wnarrowing"
#pragma GCC diagnostic ignored "-Wsign-compare"
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <random>
#define ll long long
#define rnt register int
#define gr getchar
#define pr putchar
#define N 500005
#define M 999999
using namespace std;
inline ll read()
{
int f = 1;
ll x = 0;
char ch = gr();
while (ch < '0' || ch > '9') ch == '-' ? f = -1, ch = gr() : ch = gr();
while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + (ch ^ 48), ch = gr();
return x * f;
}
inline void write(ll x)
{
static int top = 0, sta[39];
if (x < 0) pr('-'), x = -x;
do sta[++top] = x % 10, x /= 10;
while (x);
while (top) pr(sta[top--] ^ 48);
}
int top;
int stack[N][2];
int main()
{
mt19937 rand(time(0));
int n=300,cnt=2;
write(n),pr(10);write(50),pr(32);
for (rnt i=1;i<=50;i++) write(i),pr(32),write(M),pr(32),cnt+=2;
//for (rnt i=151;i<=299;i++) write(i),pr(32),write(-1),pr(32),cnt+=2;
pr(10);
for (rnt i=150;i>1;i--)
{
top=0;
stack[++top][0]=i-1,stack[top][1]=rand()%M+1;
// for (rnt j=i-2,num=0;j>=1;j--)
// if (rand()%2 && num<=8)
// stack[++top][0]=j,stack[top][1]=(rand()%M+1),num++;
write(top),pr(32),cnt++;
for (rnt i=1;i<=top;i++) write(stack[i][0]),pr(32),write(stack[i][1]),pr(10),cnt+=2;
}
pr(48),pr(10),cnt+=1;
for (rnt i=299;i>151;i--)
{
top=0;
stack[++top][0]=i-1,stack[top][1]=-(rand()%M+1);
// for (rnt j=i-2,num=0;j>=1;j--)
// if (rand()%2 && num<=9)
// stack[++top][0]=j,stack[top][1]=-(rand()%M+1),num++;
write(top),pr(32),cnt++;
for (rnt i=1;i<=top;i++) write(stack[i][0]),pr(32),write(stack[i][1]),pr(10),cnt+=2;
}
pr(48),pr(10),cnt+=1;
write(10),pr(10),cnt+=1;
for (rnt i=1;i<=10;i++) write(0),pr(32),write(150),pr(10),cnt+=2;
return 0;
}
Task 6
黎明前的黑暗……吗?观察发现 Task 4 的数据只能卡掉 dijk,所以这里也可以直接照搬,但是注意 \(T\) 的限制,把 \(q\) 改到 6 就可以了。
然后就完成了第一问!
第二问
就是个染色问题,让我们观察一下这三个代码:
- Gamble1(赌博?):耗时绝对为 0。
- Gamble2:绝对 TLE。
- RecursiveBacktracking(RB,递归回溯):唯一正常的一个,虽然是个暴力,枚举 \(X\),然后 dfs 去找。
注意这道题强行设定我们的 \(E=1501\),因为 \(E>1500\) 但是 \(T=3004\),除开输出的 \(V,E\) 就只剩下 3002,除以 2 就是 1501 了。不过终于有拟人的输出边的方式了,第一问那个什么毒瘤/fn
Task 7:
卡掉暴搜?随机图都行!
点击查看代码
//Just Sayori
#pragma GCC diagnostic ignored "-Wnarrowing"
#pragma GCC diagnostic ignored "-Wsign-compare"
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <map>
#include <random>
#define ll long long
#define rnt register int
#define gr getchar
#define pr putchar
#define N 500005
#define M 1000000007
using namespace std;
inline ll read()
{
int f = 1;
ll x = 0;
char ch = gr();
while (ch < '0' || ch > '9') ch == '-' ? f = -1, ch = gr() : ch = gr();
while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + (ch ^ 48), ch = gr();
return x * f;
}
inline void write(ll x)
{
static int top = 0, sta[39];
if (x < 0) pr('-'), x = -x;
do sta[++top] = x % 10, x /= 10;
while (x);
while (top) pr(sta[top--] ^ 48);
}
map<pair<int,int>,bool> mp;
int main()
{
int i=1;
mt19937 rand(time(0));
write(999),pr(32),write(1501),pr(10);
while (i<=1501)
{
int u=rand()%999,v=rand()%999;
if (u==v) continue;
if (u>v) swap(u,v);
if (mp[make_pair(u,v)]) continue;
write(u),pr(32),write(v),pr(10),i++;//注意要输出 1501 次
mp[make_pair(u,v)]=1;
}
return 0;
}
Task 8:
故意放过看起来很难办,但是之前我搞了个菊花图来卡,结果失败了,所以可以用它来放过暴搜。
点击查看代码
//Just Sayori
#pragma GCC diagnostic ignored "-Wnarrowing"
#pragma GCC diagnostic ignored "-Wsign-compare"
#include <iostream>
#include <cstdio>
#include <algorithm>
#define ll long long
#define rnt register int
#define gr getchar
#define pr putchar
#define N 500005
#define M 1000000007
using namespace std;
inline ll read()
{
int f = 1;
ll x = 0;
char ch = gr();
while (ch < '0' || ch > '9') ch == '-' ? f = -1, ch = gr() : ch = gr();
while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + (ch ^ 48), ch = gr();
return x * f;
}
inline void write(ll x)
{
static int top = 0, sta[39];
if (x < 0) pr('-'), x = -x;
do sta[++top] = x % 10, x /= 10;
while (x);
while (top) pr(sta[top--] ^ 48);
}
int main()
{
freopen("xx.txt","w",stdout);
int n=999;
write(n),pr(32),write(1501),pr(10);
for (rnt i=1;i<=998;i++) write(0),pr(32),write(i),pr(10);
for (rnt i=1;i<=503;i++) write(i),pr(32),write(i+1),pr(10);
return 0;
}
然后你就花了一个上午或下午或晚上或上午加下午或下午加晚上或晚上加上午或全天来完成了这道紫题!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号