C# AStar 算法 - 基本实现

算法实现代码：

代码由AI生成的

namespace Utils.AStarHelp
{
    /// <summary>
    /// 计算两个点之间的路径-现有路径计算
    /// </summary>
    public class AStarPathHelp
    {
        public static void GetPaht()
        {
            // ​​1.初始化
            ​​
            // 创建路径点网格
            List<Node> allNodes = new List<Node>();
            for (int x = 0; x < 5; x++)
            {
                for (int y = 0; y < 5; y++)
                {
                    allNodes.Add(new Node(x, y));
                }
            }
             
            // 设置障碍物（示例）
            allNodes.Find(n => n.X == 2 && n.Y == 2).IsWalkable = false;
            allNodes.Find(n => n.X == 1 && n.Y == 1).IsWalkable = false;

            // 定义起点和终点
            Node start = allNodes.Find(n => n.X == 0 && n.Y == 0);
            Node goal = allNodes.Find(n => n.X == 4 && n.Y == 4);

            // 执行A*寻路
            AStarPathfinder pathfinder = new AStarPathfinder();
            List<Node> path = pathfinder.FindPath(allNodes, start, goal, "manhattan");

            // 输出结果
            pathfinder.PrintPathInfo(path, start, goal);
        }
    }

    // 节点类，表示路径规划中的每个位置点
    public class Node : IComparable<Node>
    {
        public int X { get; }  // 节点X坐标
        public int Y { get; }  // 节点Y坐标
        public float G { get; set; }  // 从起点到当前节点的实际代价
        public float H { get; set; }  // 当前节点到终点的预估代价
        public float F => G + H;     // 总评估代价
        public Node Parent { get; set; }  // 父节点，用于路径回溯
        public bool IsWalkable { get; set; } = true;  // 是否可通行

        public Node(int x, int y)
        {
            X = x;
            Y = y;
        }

        // 重写Equals和GetHashCode，便于在集合中比较节点
        public override bool Equals(object obj) => obj is Node other && X == other.X && Y == other.Y;
        public override int GetHashCode() => HashCode.Combine(X, Y);

        // 实现IComparable接口，用于优先队列排序
        public int CompareTo(Node other) => F.CompareTo(other.F);


    }

    public class AStarPathfinder
    {
        // 启发式函数：曼哈顿距离（适用于四方向移动）
        private float ManhattanHeuristic(Node a, Node b) => Math.Abs(a.X - b.X) + Math.Abs(a.Y - b.Y);

        // 启发式函数：欧几里得距离（适用于任意方向移动）
        private float EuclideanHeuristic(Node a, Node b) =>
            (float)Math.Sqrt(Math.Pow(a.X - b.X, 2) + Math.Pow(a.Y - b.Y, 2));

        // 启发式函数：切比雪夫距离（适用于八方向移动）
        private float ChebyshevHeuristic(Node a, Node b) =>
            Math.Max(Math.Abs(a.X - b.X), Math.Abs(a.Y - b.Y));

        // 获取当前节点的所有邻居节点（四方向）
        private List<Node> GetNeighbors(Node node, List<Node> allNodes)
        {
            List<Node> neighbors = new List<Node>();
            int[] dx = { -1, 1, 0, 0 };   // 左右上下
            int[] dy = { 0, 0, -1, 1 };

            for (int i = 0; i < 4; i++)
            {
                int newX = node.X + dx[i];
                int newY = node.Y + dy[i];

                // 查找是否存在该邻居节点
                Node neighbor = allNodes.Find(n => n.X == newX && n.Y == newY);
                if (neighbor != null && neighbor.IsWalkable)
                {
                    neighbors.Add(neighbor);
                }
            }
            return neighbors;
        }


        // A*寻路主算法
        public List<Node> FindPath(List<Node> allNodes, Node start, Node goal, string heuristicType = "manhattan")
        {
            // ​2. 选择当前节点

            // 开放列表：存储待探索节点（按F值排序的优先队列）
            var openList = new PriorityQueue<Node, float>();
            // 关闭列表：存储已探索节点
            var closedSet = new HashSet<Node>();
            // 节点信息字典：记录每个节点的最佳G值和父节点
            var nodeInfo = new Dictionary<Node, (float g, Node parent)>();

            // 初始化起点
            start.G = 0;
            start.H = GetHeuristic(start, goal, heuristicType);
            openList.Enqueue(start, start.F);
            nodeInfo[start] = (0, null);

            // 7. 终止条件判断​​ 重复步骤2 - 6，直到找到目标或开放列表为空。
            while (openList.Count > 0)
            {
                // 从开放列表中取出F值最小的节点作为当前节点[1](@ref)
                Node current = openList.Dequeue();

                // 3. 目标检测

                // 如果到达终点，回溯构建完整路径
                if (current.Equals(goal))
                {
                    return ReconstructPath(current);
                }

                // 将当前节点移至关闭列表，标记为已探索
                closedSet.Add(current);

                // 4. 扩展邻居节点​

                // 遍历当前节点的所有邻居节点
                foreach (Node neighbor in GetNeighbors(current, allNodes))
                {
                    // 跳过已在关闭列表中的节点
                    if (closedSet.Contains(neighbor))
                        continue;

                    // 计算从起点经过当前节点到达邻居的新G值
                    float tentativeG = nodeInfo[current].g + 1; // 假设每步代价为1

                    // 5. 计算邻居代价
                    // 如果找到更优路径或邻居节点尚未探索
                    if (!nodeInfo.ContainsKey(neighbor) || tentativeG < nodeInfo[neighbor].g)
                    {
                        // 更新邻居节点的父节点和代价值
                        neighbor.Parent = current;
                        neighbor.G = tentativeG;
                        neighbor.H = GetHeuristic(neighbor, goal, heuristicType);

                        nodeInfo[neighbor] = (tentativeG, current);

                        // 如果邻居不在开放列表中，则加入
                        if (!openList.UnorderedItems.Any(item => item.Element.Equals(neighbor)))
                        {
                            // ​6. 更新开放列表​
                            openList.Enqueue(neighbor, neighbor.F);
                        }
                    }
                }
            }

            return null; // 未找到路径
        }

        private float GetHeuristic(Node a, Node b, string type)
        {
            return type.ToLower() switch
            {
                "euclidean" => EuclideanHeuristic(a, b),
                "chebyshev" => ChebyshevHeuristic(a, b),
                _ => ManhattanHeuristic(a, b)
            };
        }


        // 从终点回溯构建完整路径
        private List<Node> ReconstructPath(Node endNode)
        {
            List<Node> path = new List<Node>();
            Node current = endNode;

            while (current != null)
            {
                path.Add(current);
                current = current.Parent;
            }

            path.Reverse(); // 反转路径，从起点到终点
            return path;
        }

        // 打印路径和算法统计信息
        public void PrintPathInfo(List<Node> path, Node start, Node goal)
        {
            if (path == null)
            {
                Console.WriteLine("未找到可行路径！");
                return;
            }

            Console.WriteLine($"找到路径！路径长度：{path.Count - 1}步");
            Console.WriteLine("路径点序列：");

            foreach (Node node in path)
            {
                string nodeType = node.Equals(start) ? "[起点]" :
                                node.Equals(goal) ? "[终点]" : "";
                Console.WriteLine($"  ({node.X}, {node.Y}) {nodeType}");
            }

            Console.WriteLine($"起点: ({start.X}, {start.Y})");
            Console.WriteLine($"终点: ({goal.X}, {goal.Y})");
            Console.WriteLine($"总代价G: {goal.G}");
        }
    }

}

复制完直接用就可以了 调用 AStarPathHelp.GetPaht(); 即可。代码中已经标识了具体的流程和步骤。

流程说明：

 

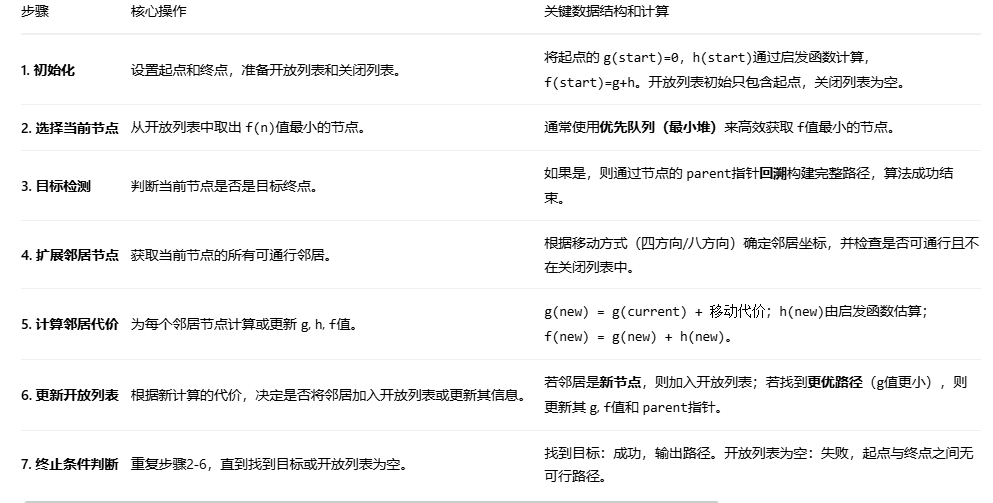
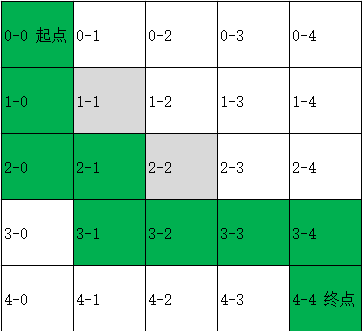
最终路径为：

 

关于距离计算方式： 默认采用 曼哈顿距离，根据实际情况 改变对应的计算方式

1. 曼哈顿距离

• 何时使用：当你的单位只能像国际象棋里的“车”一样，上下左右移动时。

• 例子：经典益智游戏《华容道》、一些简单的2D网格RPG游戏。

• 计算：从点 (1,1) 到 (4,5) 的曼哈顿距离是 |1-4| + |1-5| = 3 + 4 = 7。

2. 切比雪夫距离

• 何时使用：当你的单位可以像国际象棋里的“王”一样，向周围8个方向移动，并且对角线移动的成本与直线移动相同时。

• 例子：许多战略游戏（如《文明》系列）中的单位移动。

• 计算：从点 (1,1) 到 (4,5) 的切比雪夫距离是 max(|1-4|, |1-5|) = max(3, 4) = 4。

3. 欧几里得距离

• 何时使用：当你的单位可以在一个连续的平面上向任意方向自由移动时。这是最符合现实世界直觉的距离。

• 例子：无人机路径规划、RTS游戏（如《星际争霸》）中单位的真实移动、物理模拟。

• 计算：从点 (1,1) 到 (4,5) 的欧几里得距离是 √((1-4)² + (1-5)²) = √(9 + 16) = 5。

• 注意：在实际编程中，为了节省计算平方根的开销，有时会使用平方欧几里得距离（即 dx² + dy²）进行比较，只要保证所有 h(n) 使用相同的标准，且满足可采纳性（不高估）即可。

选择的核心原则是：你选择的 h(n) 应该尽可能接近实际成本，并且绝对不能高估实际成本。

1. 看移动规则：

   • 只能走四方向？ -> 曼哈顿距离

   • 可以走八方向，且对角线成本与直线相同？ -> 切比雪夫距离

   • 可以走八方向，但对角线成本更高（例如 √2）？ -> 可能需要使用对角距离（一种对角线和直线混合的优化距离）。

   • 可以任意方向移动？ -> 欧几里得距离

2. 看地图类型：

   • 网格化地图：优先考虑曼哈顿或切比雪夫。

   • 导航网格或连续空间：使用欧几里得距离。

 

距离参考:  欧式距离、曼哈顿距离、切比雪夫距离三种距离的可视化展示

以上内容仅仅为学习留存使用。