关于n个数进行相邻交换成升序所需最小次数

之前一直有个问题就是
n个数进行相邻交换成升序所需要的最小次数一定就是等于逆序对数量吗？

后来渐渐发现确实如此，但是分情况

• n个不同的数

1 5 2 3 4

那么最优或者说贪心因该怎么交换呢？其实这种情况最好说明，由于这n个数互不相同
，每次交换要么两种情况
1.逆序对数+1，正序对数-1
2.正序对数+1，逆序对数-1
对于最优解我们优先或者说我们只进行2类操作。

在解释之前进行补充
在上述样例中所有逆序对数如何简单暴力，又不重复求？
这里不讨论merge排序求，因为只能给你一个结果不能具现的表示出来
逆序对的定义无非是存在i < j, 满足a[i] > a[j];
我们固定右边的j，判断小于j的所有索引如果a[i] > a[j]那么<i, j>就是一个逆序对了
这个固定的方法最近发现很多地方特别有用，很值得学习。
那么对于样例即有如下

那么最优解就是只进行2操作，第一步只能进行索引<2,3>交换
1 2 5 3 4
1 2 3 5 4
1 2 3 4 5
再来一个样例

1 2 3 5 8 7 4 6

1 2 3 5 7 8 4 6
1 2 3 5 7 4 8 6
1 2 3 5 4 7 8 6
1 2 3 4 5 7 8 6
1 2 3 4 5 7 6 8
1 2 3 4 5 6 7 8 可以验证6即为逆序对数量，也就是表示只进行减少逆序对数量的操作即为最少次数

• 含有相同数字也类似，逆序对定义相同，也是只进行2类操作
  样例

1 5 3 2 5 2

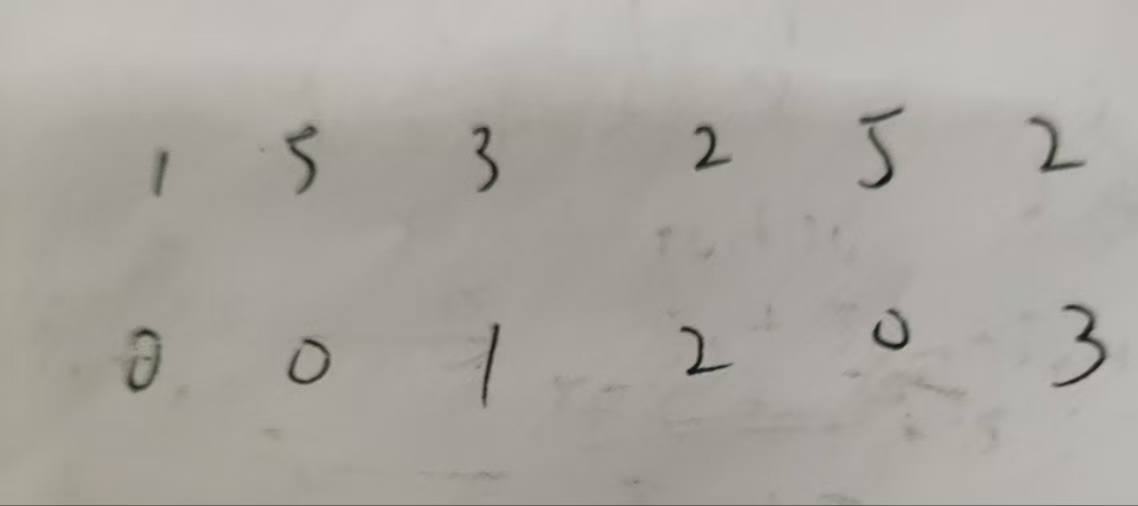
1 3 5 2 5 2
1 3 2 5 5 2
1 3 2 5 2 5
1 3 2 2 5 5
1 2 3 2 5 5
1 2 2 3 5 5 和总逆序对数相同