折半搜索（2 ^ 40 分成 2 ^ 20 + 2 ^ 20)

今天又学到一个优化思路，折半搜索，对于方案搜索问题，我们往往会想到暴力搜索（O（2 ^ n))，最多想到01背包(O(n * m))
1s限制这时候暴力搜索大致可以过n <= 20, 01背包大致可以过n * m <= 1e9, m为背包最大容量
来题

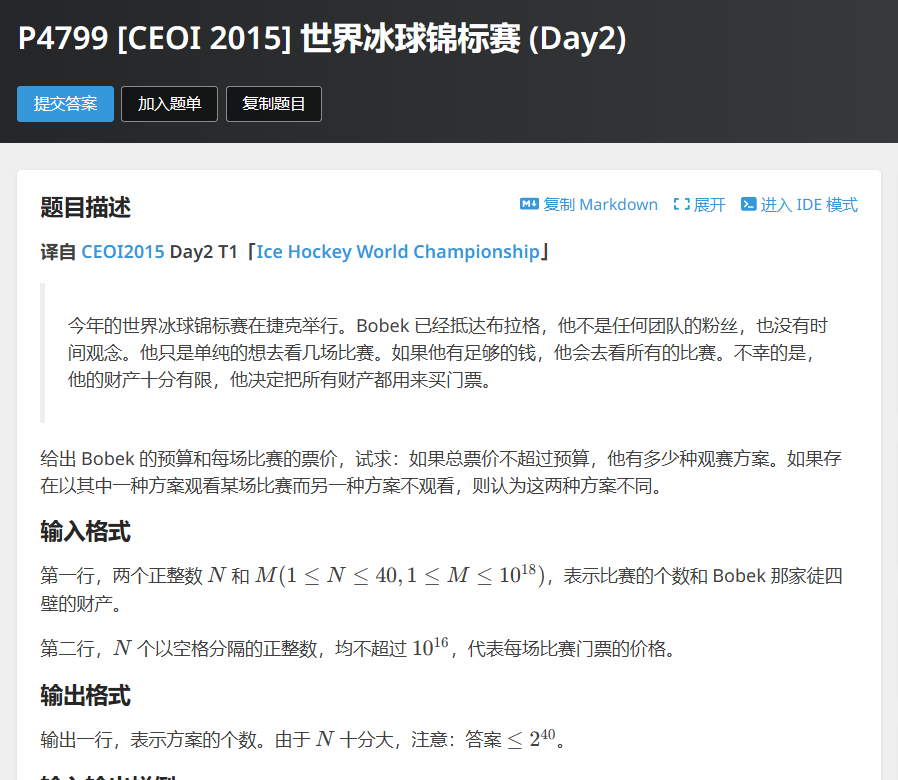
这时候n <= 40, m <= 1e18,背包和爆搜都会tle。

引入一个折半搜索（使用要求，前半段和后半段可以整合）
代码如下

#include
#define int long long 

using namespace std;

const int N = 44;
int t[N], cnta, cntb;
int a[N], b[N];
int n, m;

void dfs(int l, int r, int* arr, int sum, int& cnt) {
	if (sum > m) return;
	if (l > r) {
		arr[++cnt] = sum;
		return;
	}
	dfs(l + 1, r, arr, sum + t[l], cnt);
	dfs(l + 1, r, arr, sum, cnt);
}
signed main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> t[i];
	int mid = 1 + n >> 1;
	dfs(1, mid, a, 0, cnta);
	dfs(mid + 1, n, b, 0, cntb);
	sort(a + 1, a + cnta + 1);
	int ans = 0;
	for (int i = 1; i <= cntb; i++) {
		ans += upper_bound(a + 1, a + cnta + 1, m - b[i]) - a - 1;
	}
	cout << ans << endl;
	return 0;
}

思路是将40个变量分成两个20个，所以暴力之后就是2 * (2 ^ 20), 但是这么做肯定有要求，前面能和后面整合，这道题目整合就是a数组中的方案总价值和后面的b数组中的价值相加小于等于m，可以用二分查找上界，现在想想这个折半搜索是真的秒。时间复杂度大约2 * （2 ^ 20)

https://www.luogu.com.cn/problem/P3067