扩展欧几里得
//20250512再次学习修改一堆毛病/(ㄒoㄒ)/~~
下面我梳理一下有几个证明,(1),(2)
我们知道欧几里得算法就是辗转相除法
(1)简单证明一下gcd(a, b) = gcd(b, a % b);

int gcd(int a, int b){
return (!b ? a : gcd(b, a % b));
}
欧几里得算法:一定存在x, y属于Z使得ax + by = gcd(a, b);
我们现在探讨的是扩展欧几里得,使用在具有(ax + by = m)中求满足的x和y的有正整数解的充要条件是m % gcd(a, b) = 0,
(2)证明,a, b是gcd(a, b)的倍数,如果x和y也要是正整数那么m一定是gcd的倍数
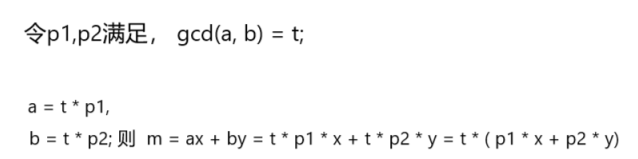
代码如下
这里是求ax + by = gcd(a, b) 中 x, y的值
int x, y;//全局变量
int exgcd(int a, int b){
if(!b) {
x = 1, y = 0;
return;
}
exgcd(b, a % b);
int t = x;
x = y;
y = t - (a / b) * y;
}
离散数学中是这样赘述的,也可以靠这个理解一下欧几里得


之前的版本是借鉴大佬的,现在完全理解可以自己想出来怎么反向构造系数了。
这里两个参数分别用n1, m1表示, 参数用两个系数表示s1, t1, 也就是n1s1 + m1t1 = gcd(n1, m1)
从最后开始求gcd(n1, m1), 当m1 = 0时, gcd(n1, 0) = n1. 在这里构造的系数n1 * s1 + m1 * t1 = n1可以是(1, 0)挑最简单的。
然后需要反求倒数第二个等式的系数。可以知道假设是gcd(n0, m0) = gcd(m0, n0 % m0), 所以上式等式 n1 = m0, m1 = n0 % m0, 等式变为m0 * s1 + n0 % m0 * t1 = gcd
我们需要把等式变成n0 * s0 + m0 * s0 = gcd的形式由n0 % m0 = n0 - (n0 / m0) * m0,整理获得n0 * t1 + m0 * (s1 - (n0 / m0) t1) = gcd
因此,我们想从下一个等式的参数获得本等式的参数,只需要
{
int tem = s;
s = t;//把第二个赋值给第一个参数。
t = tem - (n / m) * t;
}
如下我开始展示如何手算贝祖系数
有如下例子,n = 120, m = 23;
120 = 23 * 5 + 5;
23 = 5 * 4 + 3;
5 = 3 * 1 + 2;
3 = 2 * 1 + 1;
2 = 1 * 2;
将余数提前,获得如下等式
(1)5 = 120 - 23 * 5;
(2)3 = 23 - 5 * 4;
(3) 2 = 5 - 3 * 1;
(4) 1 = 3 - 2 * 1;
(5) 0 = 2 - 1 * 2;
综上,gcd(120, 23) = 1;
(1)式已经由120 和 23组成
(2)式减数的5由1式代入获得3 = 23 * 21 - 120 * 4;
(3)式被减数的5由(3 - 2)式代入,减数的3用(3 - 1)式代入
(4)式的被减数的5由(4 - 2)式代入,减数的2用(4 - 1)式代入
由于(4)式就是gcd = n * s + m * t的形式,所以没必要再套下一层了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号