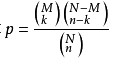概念/公式 积累

范德蒙德卷积
\(\sum_{i = 0}^{k} \tbinom{n}{i} \tbinom{m}{k - i} = \tbinom{n + m}{k}\)

斯特林数
link

\(\tbinom{n}{m} \tbinom{m}{k} = \tbinom{n}{k} \tbinom{n - k}{m - k}\)

超几何分布（Hypergeometric Distribution ）
从有限N个物件（其中包含M个指定种类的物件）中抽出n个物件，成功抽出该指定种类的物件的次数（不放回），记作X~H(N,M,n)

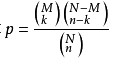
\(x^k = \sum_{i = 0}^{x} \tbinom{x}{i} i! S(k, i)\)

\(\sum_{i = 1}^{n} \sum_{j = 1}^{i} = \sum_{j = 1}^{n} \sum_{i = j}^{n}\)

题目
luogu2791幼儿园篮球题