ZROI暑期夏令营C班ACM赛

为了气球溜到C班玩acm 结果身败名裂
记住，三角形面积是 x × y + y × z + z × x
几道比较有趣的题

C

动物园最近举行了选举。总共有7个主要的政党:其中一个是小象党，另外6个政党的名字不那么好听。 政党发现他们的竞选编号非常重要。总共有m个可能的编号:1、2、……、m。这7个参与方中的每一个都将以某种方式被分配到一个编号上，在这种情况下，两个不同的参与方不能接收到相同的编号。 小象党成员相信幸运数字4和7。他们想要评估他们在选举中的机会。为此，他们需要找出，有多少个正确的分配使得小象政党的竞选编号中的幸运数字数位的数目严格大于其他6个政党的竞选编号中的幸运数字的总数。 请你帮小象政党算一下这个数字。由于答案可能相当大，所以将其除以1000000007(10^9 + 7)后的余数输出。
Input
单行包含一个正整数m(7≤m≤10^9)——竞选编号中可能出现的数字。
Output
一行一个答案，表示所有满足条件的分配方案在模10^9+7意义下的值。
Examples
样例输入1
7
样例输出1
0
样例输入2
8
样例输出2
1440

打了一个数位dp然后组合一下剩下六个人
然后自闭了（因为没有看到"总数"

贴一发正解

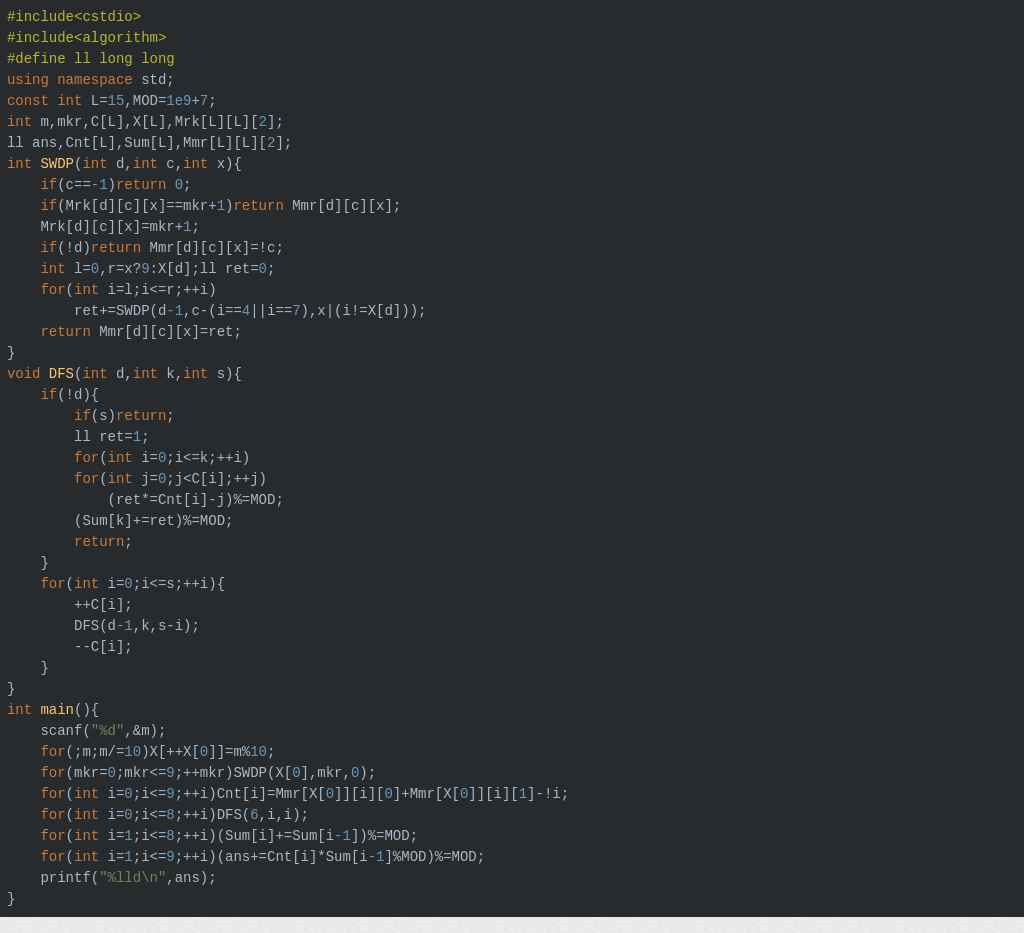
H

ZhengRuCaiLaoBan有一个栈。此问题中的栈是支持两个操作的数据结构。操作push(x)将一个整数x放在栈的顶部，操作pop()从栈中删除顶部整数，即最后添加的整数。如果栈是空的，那么pop()操作什么也不做。
ZhengRuCaiLaoBan对栈进行了m次操作，但是忘记了这些操作。现在他想要回忆他的操作序列。他一个接一个地记起了这些操作，在第i步他记起了他做的第pi步操作。换句话说，他记得的运算顺序是p1 p2…pm。ZhengRuCaiLaoBan在执行了他已经记住的操作之后，按照相应的顺序，在每一步之后，他都想知道栈顶部的整数是多少。请你帮助他!
Input
第一行包含整数m(1≤m≤10^5)——ZhengRuCaiLaoBan执行的操作数。
接下来的m行包含ZhengRuCaiLaoBan记起来的操作。第i行两个整数pi和ti(1≤pi≤m, ti = 0或ti = 1)表示他记得第pi步的类型为ti。ti = 0表示操作是pop()，ti=1表示push(x)。如果操作是push(x)，则该行中包含第三个整数xi(1≤xi≤10^6)表示添加到栈中的整数。保证从1到m的每一个整数恰好出现一次。
Output
输出m行每行一个整数。 第i行输出ZhengRuCaiLaoBan在执行了从1到i的步骤中记起的所有操作之后，栈顶部的数字。如果在执行所有这些操作之后栈是空的，那么输出-1。
Examples
样例输入1
2
2 1 2
1 0
样例输出1
2
2
样例输入2
3
1 1 2
2 1 3
3 0
样例输出2
2
3
2
样例输入3
5
5 0
4 0
3 1 1
2 1 1
1 1 2
样例输出3
-1
-1
-1
-1
2
Note
在第一个样例中，ZhengRuCaiLaoBan记住第一步的操作后，操作push(2)是唯一的操作，所以答案是2。当他记住在push(2)之前执行的pop()操作后，答案保持不变。 在第二个样例中，操作是push(2)、push(3)和pop()。 在第三个例子中，ZhengRuCaiLaoBan以相反的顺序记起操作。

pop记作-1 push记作1 求最后一个为1的后缀

I

ZhengRuCaiLaoBan非常喜欢红色，但他并不喜欢蓝色。 ZhengRuCaiLaoBan站在一个无垠的田野里，那里有n个红点和m个蓝点。 ZhengRuCaiLaoBanw希望在田野中绘制一个圆圈，使这个圆圈包含至少一个红点，而没有蓝点。恰好在圆的边界上的点可以被计算在内也可被计算在圆外。 请你计算满足这个条件的最大圆的半径。如果这个圆可以任意大，输出 -1。否则，你的答案将判为正确，当且仅当它与正确答案的相对或绝对误差不超过10^- 4。
Input
输入的第一行包含两个整数n, m(1≤n, m≤1,000)。
接下来的n行包含两个整数xi, yi(1≤xi, yi≤10^4)。表示一个红点的坐标。
接下来的m行包含两个整数xi, yi(1≤xi, yi≤10^4)。表示一个蓝点的坐标。
没有两个点有相同的坐标。
Output
如果这个圆可以任意大，那么输出-1，否则输出这个圆的最大半径。如果你与答案的绝对或相对误差不超过 10 - 4即被判为正确.
具体而言，假设你的答案是a 正确答案是 b. 那么你的答案会被判对当且仅当.
Examples
样例输入1
2 5
2 3
3 4
1 1
1 4
4 2
4 7
2 5
样例输出1
3.5355338827
样例输入2
1 6
3 3
1 5
5 4
2 1
3 4
4 2
1 3
样例输出2
1.5811388195
样例输入3
2 2
2 2
3 3
1 1
4 4
样例输出3
-1
Note
第一个样例的示意图：

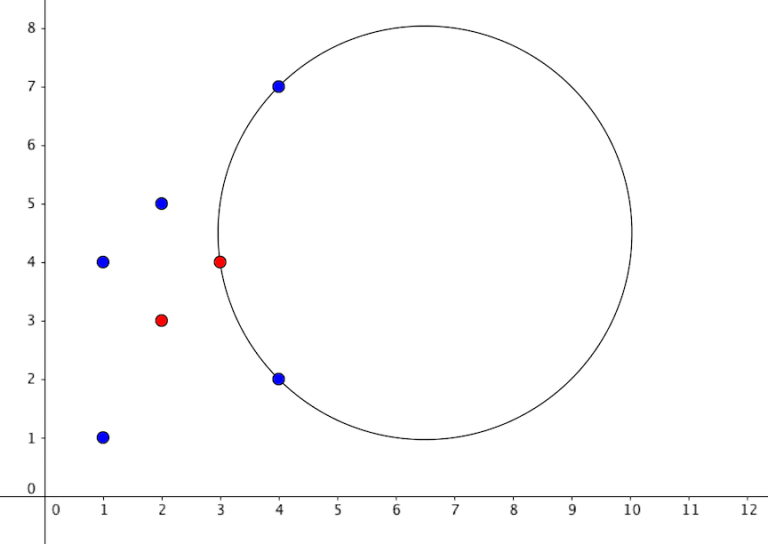
第二个样例的示意图：

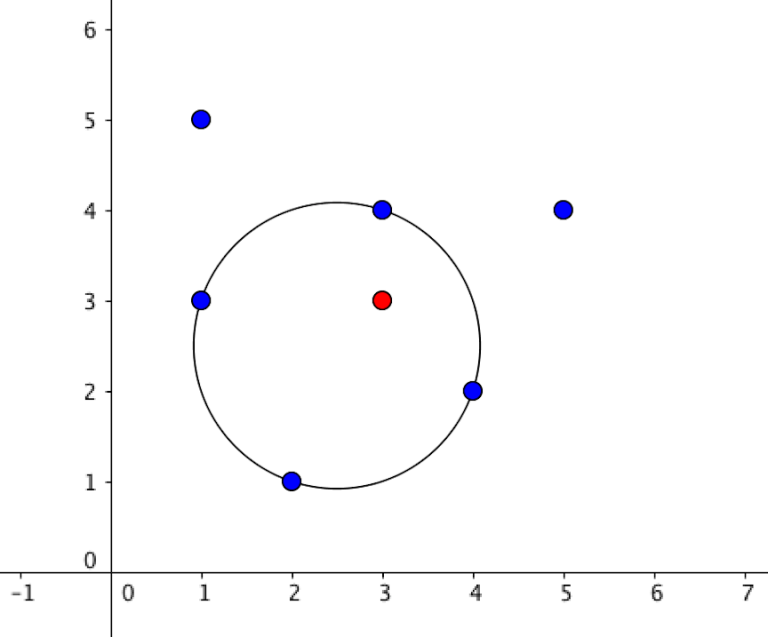
二分枚举半径
check:
对于每对蓝点红点得到两个圆的交点 判断这些点所在的圆是否包含蓝点
然后对每个红点看是否有不交蓝点的圆

B

ZhengRuCaiLaoBan想要最小化一棵树。他可以多次执行以下操作:选择一个顶点v，和两条长度相等、除了v外不相交的路径a0 = v, a1，…， ak, b0 = v, b1，…， bk，此外，顶点a1，…， ak, b1，…， bk在树中除了所在路径的相邻顶点外，不能有任何邻居。（邻居即为通过一条边直接相连的点对）然后，其中一条路径可以合并到另一条路径中，即顶点b1，…， bk可以有效擦除，如图所示:

帮助ZhengRuCaiLaoBan确定是否可以通过一系列上面描述的操作将一棵给定的树转换为路径，如果答案是肯定的，还请继续确定该路径的最短长度。
Input
输入的第一行包含顶点数n(2≤n≤2*10^5)。 接下来的n - 1行描述了这棵树。每一行包含两个空格分隔的整数u和v(1≤u, v≤n, u≠v)，表示树上的一条边。
Output
如果无法通过题面中的操作得到路径，那么输出-1，否则输出最短的路径长度。
Examples
样例输入1
6
1 2
2 3
2 4
4 5
1 6
样例输出1
3
样例输入2
7
1 2
1 3
3 4
1 5
5 6
6 7
样例输出2
-1
Note
在第一个例子中，将路径2 - 1 - 6和2 - 4 - 5合并后得到一个长度为3的路径。
在第二个样例中不可能执行任何操作。例如，不可能合并路径1 - 3 - 4和路径1 - 5 - 6，因为顶点6还有一个邻居7，它不在对应的路径中。