https://blog.csdn.net/luoluonuoyasuolong/article/details/90711318
PCA 用来干什么？
PCA呀，用来做什么呢？这个很重要，PCA也有很多应用，可能我们之前听过用PCA做人脸识别，PCA做异常检测等等。但事实上PCA没有那么强大的功能，PCA能做的事其实很有限，那就是：降维。其他拓展应用都是在这基础上做了相应额工作。为什要降维呢？很明显，数据中有些内容没有价值，这些内容的存在会影响算法的性能，和准确性。
如上图，数据点大部分都分布在x2方向上，在x1方向上的取值近似相同，那么对于有些问题就可以直接将x1坐标的数值去掉，只取x2坐标的值即可。但是有些情况不能直接这样取，例如：
上图的数据分布在x1和x2方向都比较均匀，任一去掉一个坐标的数值可能对结果都会有很大的影响。这个时候就是PCA展现作用的时候了。黑色坐标系是原始坐标系，红色坐表系是我后面构建的坐标系，如果我的坐标系是红色的，那么这个问题是不是就和上面那个问题一样了，我只需要去掉y2坐标系的数据即可。实际上黑色坐标系和红色坐标系是等价的，差异仅仅是在空间中他们的基不同，黑色坐标系的基是我们最习惯的(1, 0), (0, 1)，红色坐标系的基是(1, 1),(-1, -1)，事实上，他们是等价的，只不过经常默认使用的就是黑色坐标系。主成分分析可以让数据的投影到那些数据分布比较分散的平面上，比如上图的y1，从而忽视y2的作用，进而达到降维的目的。
PCA 数学原理
为了达到目的，可以不择手段
上面我们说PCA可以将数据投影到分布分散的平面内，而忽略掉分布集中的平面。我们可以这样理解，如上面的图2,大部分数据投影到y1坐标系中的化，数据分布会比较分散，投影到x1、x2等其他坐标轴分布会相对集中，其中，投影到y2上面分布最集中。所以我们尽可能将数据转化到红色坐标系，然后去掉y2坐标。好了，问题描述完了，该想象怎样才能达到这样的目的。
任何形式的变化在数学上都可以抽象成一个映射，或者函数。好，现在我们需要构建一个函数f(Xm×n) f(X_{m\times n})f(X
m×n
)使得这个函数可以将矩阵Xm×n X_{m\times n}X
m×n
降维，矩阵X XX是原始数据，矩阵的每一行是一个样本的特征向量，即矩阵Xm×n X_{m\times n}X
m×n
中有m个样本，每个样本有n个特征值。所以，所谓的降维，其实是减少n的数量。
假设降维后的结构为Zm×k Z_{m \times k}Z
m×k
，其中k<n k < nk<n
那么PCA的数学表达可以这样表示：
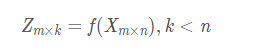
这里可能比较抽象，我尽量说得有趣：
开始数学了，手段是数学
参考资料：
李宏毅机器学习：PCA
Reducing the Dimensionality of Data with Neural Networks
掌管天堂的空之王者，于地狱唱响容光之歌！
————————————————
版权声明：本文为CSDN博主「小猪嘎嘎」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/luoluonuoyasuolong/article/details/90711318
