SAM

其结构包含两部分：有向单词无环图（\(\texttt{DAWG}\)）以及一棵树（\(\texttt{parent}\)树）。

它们的节点集合相同。

目标：最小化节点集合大小！

DAWG

\(\texttt{DAWG}\)是\(\texttt{DAG}\)，其中每个节点表示一个或多个\(\texttt{S}\)的子串。特别地，起始节点对应\(\varnothing\)。

每条转移边上仅有一个字符。从起始节点出发，沿着转移边移动，则每条路径都会唯一对应\(\texttt{S}\)的一个子串。

每个节点所代表的字符串是\(\texttt{S}\)的某个前缀的长度连续的后缀。设\(\texttt u\)的长度最小、最大的子串分别为\(\min_u\)和\(\max_v\)，\(\max_u\)在\(\texttt S\)中出现的位置集合为\(end_u\)。

定理

任意两个节点的 end 集合互不相同。

parent 树

定义

定义\(\texttt u\)的\(\texttt{parent}\)指针指向\(\texttt v\),当且仅当\(|\min_u|=|\max_v|+1\)，且\(\texttt v\)所代表的子串均为\(\texttt u\)子串的后缀，记作\(next_u=v\)。

显然，所有节点沿着\(\texttt{parent}\)指针向前走，都会走到\(\texttt{DAWG}\)的起始节点。因此以\(\texttt{parent}\)指针为边，所有节点组成了一棵树，称为\(\texttt{parent}\)树。

定理

在\(\texttt{parent}\)树中，子节点的\(end\)集合一定是父亲的真子集，即\(end_u \subset end_{next_u}\)。

构建：增量法

\(\texttt{SAM}\)的构建使用增量法：通过\(\texttt S\)的\(\texttt{SAM}\)求出\(\texttt{S+c}\)的\(\texttt{SAM}\)。

设此前表示\(\texttt S\)的节点为\(\texttt p\)，\(\texttt{parent}\)树上从\(\texttt p\)到起始节点的路径为

\(v_1=p,v_2,\cdots,v_k\)，则一定存在一个\(\texttt i\)，使得\(v_1\)~\(v_i\)都没有\(\texttt c\)的转移边：

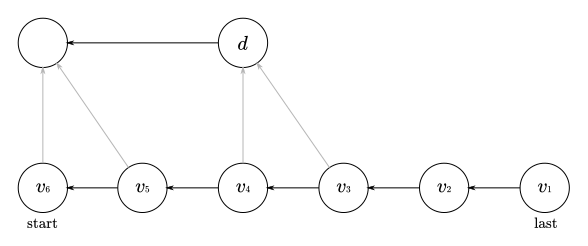
若\(v_i\)有\(\texttt c\)的转移边，则\(v_{i+1}\)也必有，故没有\(\texttt c\)转移边的点是\(\texttt v\)序列的一个前缀：在这个例子中为\(v_1\)~\(v_2\)。

（注：由于\(\max_{v_5}+c\)属于白板，\(\min_{v_4}+c\)属于\(d\)，且\(v_4\)是\(v_5\)的\(\texttt{parent}\)，所以有\(|\max_{v_5}|+1=|min_{v_4}|\)，所以\(d\)的\(\texttt{parent}\)为白板。）

\(v_1\)~\(v_2\)添加\(\texttt c\)得到的是新串长度连续的后缀，用新节点\(\texttt u\)表示，则：\(\max_u=\max_{v_1}+\texttt c,\min_u=\min_{v_2}+\texttt c\)。

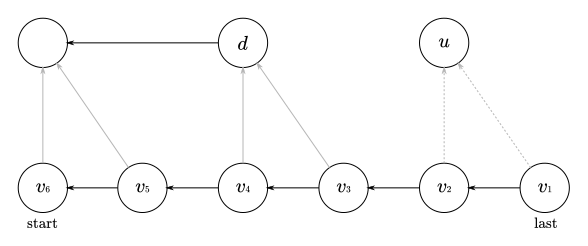
共新增了\(\texttt{|S|+1}\)的后缀，节点\(\texttt u\)表示了\(\min_u\)及更长的后缀，而更短的那些可以由\(d\)及其后缀链接上的路径上的节点来表示。

（注：这里\(v_1\to v_2,v_3\to v_4,v_5\to v_6\)中间实际上可能有很多点,如\(v_{1.5},v_{3.4},v_{5.6}\)之类的，

因此\(\texttt{DAWG}\)的性质已经被满足，接下来考虑\(\texttt{parent}\)树。

分三种情况讨论：

第一种情况

• 不存在图中的\(v_3\)。（即所有的点都没有到\(\texttt c\)的一个转移边）.

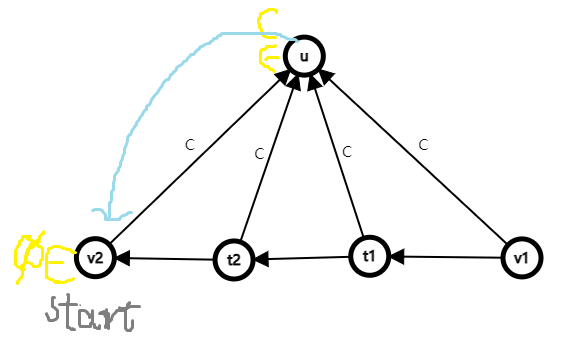
建一个新节点\(\texttt{u}\),代表\(\texttt{S+c}\)串的所有后缀（最短串为\(\texttt c\)），既然最短的串只有一个字符那么它的\(\texttt{parent}\)为只能有\(0\)个字符的东西，空串由起始节点代表，所以新节点\(\texttt u\)的\(\texttt{parent}\)指针应该指向\(\texttt{start}\)节点。

• 当\(v_3\)存在时，分\(\max_d\)是否等于\(\max_{v_3}+C\)两种情况讨论

（这里黄色代表\(\texttt{DAG}\)上的，绿色代表\(\texttt{parent}\)树上的。）

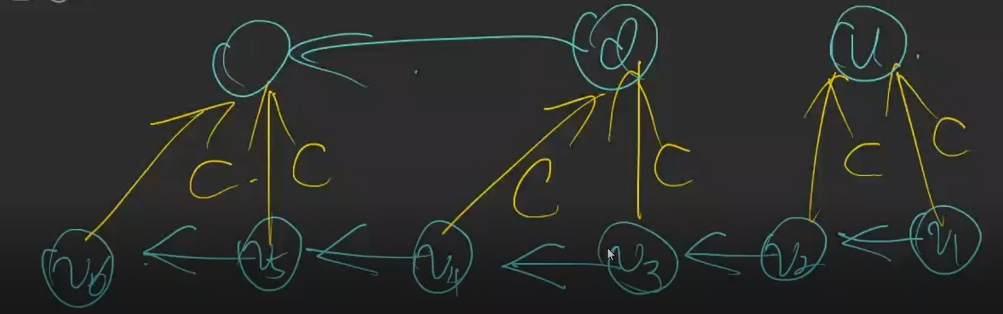
如现在有串\(\texttt {S=cbabba}\)

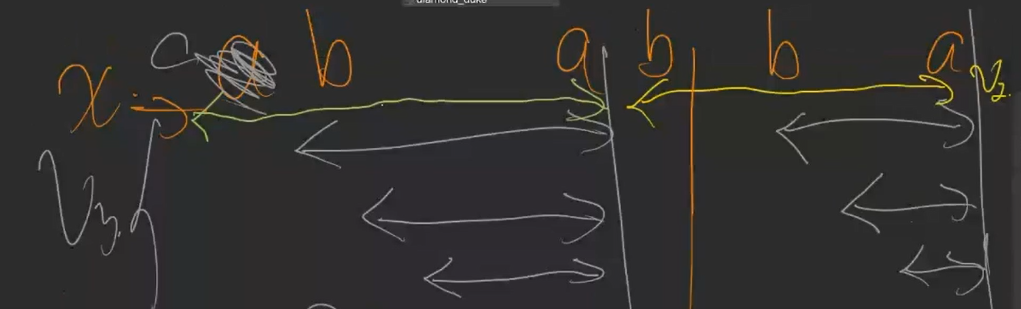
此时假设\(\texttt x\)为绿色这一段，此时新增一个\(\texttt b\)

\(x\to \texttt{bab},\texttt{end={4}}\)

\(v_3 \to \texttt {bab,ab,end={4}}\)

因为这两个集合一样，因此将会被合为一个节点，假设这个节点为\(\texttt d\)。

那么这个\(x\)点\(+c\)转移到的是\(\texttt d\)，且\(x\)点的父亲也是\(\texttt d\)。

那么就会变成这个样子,这时候会产生一个问题

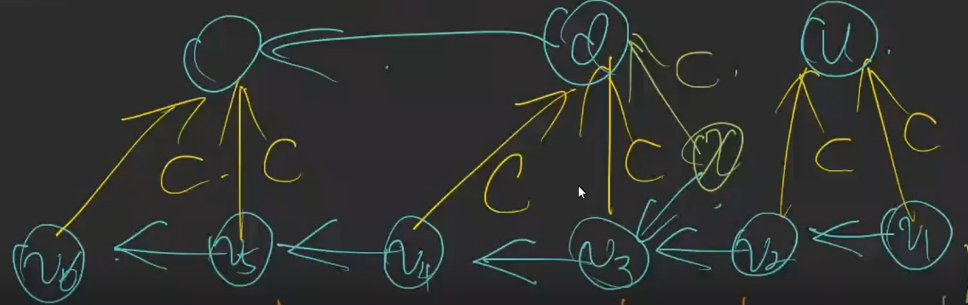
考虑新加进来了字符\(b\)

那么\(v_3\)集合的\(\texttt{bab,ab}\)变了，而\(\texttt{end={4,7}}\)。

那么此时就要将\(x\)和\(v_3\)切开。

而当\(max_d=max_{v_3}+C\)时，即不存在这样的\(x\)节点。

此时情况比较简单因为我们不用拆这个点。

此时考虑一下\(\texttt{u}\)和\(\texttt{d}\)的关系。（猜一下\(\texttt u\)的父亲是\(\texttt d\)。）

证明：

首先\(\texttt d\)的所有串是\(\texttt u\)的后缀，并且需要考虑一下长度是否吻合。（这里猜一下是吻合的。）

这里稍微推一下：

\(\begin{align} |max_{d}| & = |max_{v_3}+1| \\ & = |min_{v_2}|-1+1 \\ & = |min_u| -1 \\ \end{align}\)

所以\(u\)的\(\texttt{parent}\)应指向\(d\).

那么当\(\max_d \not= \max_{v_3}+C\).

考虑\(d\)中的串怎么切。

假设被分割后的集合为\(x+C\)和\(v_3+C\)。（两个集合拼起来为\(d\).）

用\(d'\)表示\(x+C\),用\(v\)表示\(v_3+C\)。

首先\(d'\)的\(\texttt{parent}\)指针应该指向\(v\)，然后\(v\)的\(\texttt{parent}\)指向原\(v_3\)指向的东西。

对于原来\(\texttt{parent}\)指向\(d\)的应该都指向\(d'\)。（因为\(d'\)保留了最长串，而\(\texttt{parent}\)是按照最长串定的）。

然后\(u\)的\(\texttt{parent}\)应该指向\(v\)。

关于新建节点。

在实际操作中，每一个点需要存\(\max,\min,end,next\)。

而\(\max\)直接存长度即可，因为可以从\(end\)集合取一个\(|\max|\)的再随便弄一个下来就是\(\max\)了。

而\(\min\)可以不存，因为它一定是\(next\)的\(\max\)加上什么东西。

（因为有\(end\)集合所以有长度集合就可以知道有什么串）

\(end\)与其说是存整个集合一般情况为只存第一个出现（即\(end\)集合最小的数）。要得到完整的\(end\)集合直接在\(\texttt{parent}\)树上所有子树上的拼起来就得到了。所以\(end\)也只需要存一个数。

伪代码

空间复杂度是线性的：

证明：

节点数肯定是线性的，因为一次新建一个\(u\)，然后把\(d\)拆成两个点，所有说每次最多加\(2\)个点，最后总的节点数一定不到\(2\)倍的字符串长度。

\(\texttt{parent}\)树的边数也一定是线性的，因为\(\texttt{parent}\)树是一棵树，边数等于点数\(-1\)。

接下来考虑\(\texttt{DAWG}\)，考虑给\(\texttt{DAWG}\)搞一棵生成树，对于一条非树边\(u\to v\)，来拼一个字符串，沿着树边走到\(u\)，再沿着非树边走到\(v\)，接着随便走，（比如以字典序最小）走到一个终态。我们会经过若干条边，将这些边首尾相连就得到了一个字符串\(w\)，记作\(f(u,v)\)。（因为是树，所以沿着树边到\(u\)是唯一的，\(u\to v\)是唯一的，接下来每一步以字典序最小走也是唯一的）。

\(f(u,v)=w\)，\(w\)一定是\(s\)的一个后缀，因为走到接受态（接受态经过的所有东西都是后缀）。由于给出\(f(u,v)\)能求出唯一的\(w\)，给出\(w\)不一定能求出\(f(u,v)\)，所以\(|u\to v|\leq |w|=|s|\)，所以\(|u\to v|\)的数量是\(\leq\)串长的，所以非树边的个数是小于串长的，然后树边的个数是线性的，所以最后总的边数也是线性的。

所以空间复杂度是线性的。（用到的部分）。

时间复杂度是线性的：

懒得证了...

就大概第一个循环考虑\(|\max_{next_{last}}|\)，第二个考虑\(|\min_{next_{last}}|\)。

然后复杂度可能还有考虑如何复制边的复杂度。