杂题随机做1
2020 ICPC 上海赛区
官方题解:https://zhuanlan.zhihu.com/p/336649300
gym102900L.Traveling in the Grid World
简要题意
平⾯⽆限⼤格点图,从\((0,0)\)⾛到\((n,m)\),每次只能从⼀个格点⾛⼀条线段到另⼀个格点,且线段不能经过其他格点。求最短路径⻓度。注意相邻两条线段斜率不同\((x_0-x_1 )(y_1-y_2)\neq (x_1-x_2)(y_0-y_1)\).
\(n,m\leq 10^6\),但是可以做到\(n,m\leq 10^{18}\)
sol:
Hint 1:多段折线有可能更优吗?调整法遇到不合法线段怎么办?请给出证明。
结论就是折线段数不超过两段。
证明考虑调整法:
如果有相邻两步在同一侧的话
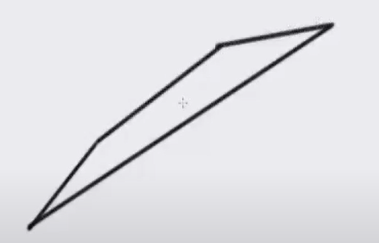
那么考虑将相邻两步合成一条,但是这样的话可能上面会有格点:
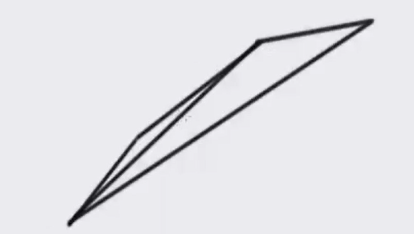
那么考虑找到任意一个可以走的格点再缩下来:

然后一直这么重复下去,最后就肯定再也没有格点了。
这就说明有相邻两步在同一侧是不存在的
如果是有在不同侧的话:
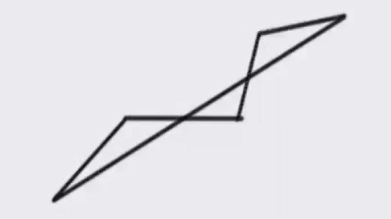
那么可以直接给出更优的一段线段:
可以先选择一个格点,然后直接往两端拉
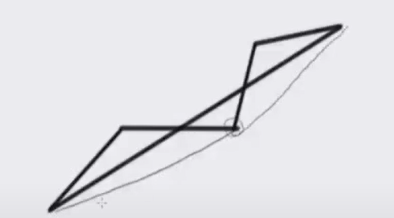
如果这个格点不合法,那么还可以将他拉得更短。
也就是说如果线段不合法一定可以让他的面积变小,然后这样子长度也会变短(这里涉及到一个定理:如果一个凸多边形严格包含另一个凸多边形,那么外面那个凸多边形的周长一定是大于等于里面的凸多边形的),且由于面积不会变为\(0\),所以结束的时候它一定是合法的。
 \(\to\)
\(\to\) 
所以说如果从一个点到另外一个点花了三步走的话是一定可以把他变成更短的两步的。
首先如果三角形有包含关系,那么外面的三角形一定比里面的劣:
而\(10^6\)做法为考虑对于每一条竖着的线,然后找出最靠近直线的两个格点,然后检查答案就行了
然后再来考虑\(10^{18}\)次方怎么做
Hint 2:考虑选择的格点到直线的距离?任意格点到直线的距离和最小距离的关系?
考虑表示\((0,0)\to (n,m)\)一条直线上所有的点,然后求出这条直线的法线。
然后用点积的形式把他写出来
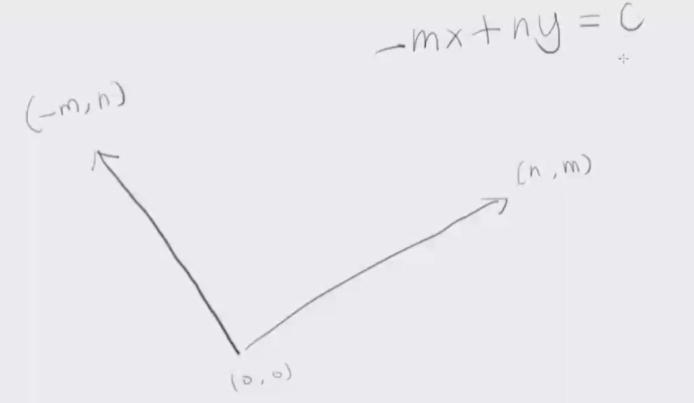
其中\(-mx+ny=c\)表示一条与\((0,0)\to (n,m)\)平行的直线(\(c=0\)时就是这条直线)意义可以看成\((-m,n)\cdot (x,y)=c\)的点积的意义就是可以看成两个向量的投影。

相当于格点到直线的距离\(=\frac{c}{\sqrt{n^2+m^2}}\)。
然后当\(m,n\)不互质时并不是对于所有的\(c\)都是整数解。
那么考虑称原来的为\(M,N\),然后将除以\(\gcd(M,N)\)的为\(m,n\)。
此时对于任意的\(c\)都是整数解,考虑\(c=1\)时是最靠近原来直线的一条直线,然后上面也有一些格点,现在有一个结论就是最优的转折点一定在\(c=1\)这条直线上

即\(-mx+ny=1\),且\(\gcd(m,n)=1\)
可以考虑如果\(c\neq 1\)的情况,由于\(c>0\)与\(c<0\)是对称的所以只讨论\(c>0\)的情况。
首先任意\(c>1\)的的格点到直线的距离一定是最短距离的整数倍,并且\(c>1\)的格点一定包含\(c=1\)的格点。
假设\(\gcd(M,N)=g\),那么这个直线一定可以表示成\(g\)段\((m,n)\),然后可以知道对于\(-mx+ny=c\)这个式子的解集,相邻两个解集的差一定是\(m\)和\(n\),相当于\(x'=x+n,y'=y+m\)。就是说它的排列方式与\(c=1\)一样,但是被位移了一段距离。
也就是说任意\(c>1\)的格点组成的三角形与\(c=1\)这条直线的交是大于等于它的一倍周期的,所以一定是不优的。

所以实际上它是一个模意义下的方程\(ny\equiv c \pmod m\)。
\(y\)每隔\(m\)就有一个解,而\(x=\frac{ny-c}{m}\)。
而\(n,m\)互质,所以一定存在逆元。
所以\(y=c\cdot n^{-1}\)这就是一个解,而\(y+m\)也是一个解。
然后具体就是按照\(c=1\)那条直线对称一下,选交点,然后在交点两边相邻格点看下答案就是了。(靠交点距离越近路径越短)

int exgcd(int a,int b,int &x,int &y){if(!b){x=1,y=0;return a;}int ret=exgcd(b,a%b,y,x);y-=a/b*x;return ret;}
double get_dis(int x,int y){return sqrt((double)(1.0*x*x+1.0*y*y))+sqrt((double)(1.0*(N-x)*(N-x)+1.0*(M-y)*(M-y)));}
signed main()
{
for(int _=read();_;_--)
{
N=read(),M=read();
int g=exgcd(M,N,x,y);
if(g==1) {printf("%.12f\n",sqrt(double(1.0*N*N+1.0*M*M)));continue;}
n=N/g,m=M/g;
int r=x/n-1;
x=-x;
x+=r*n,y+=r*m;
r=(N*N+M*M-(x*N+y*M)*2)/(N*n+M*m)/2;
x+=r*n,y+=r*m;
double ans=get_dis(x,y);
ans=min(ans,min(get_dis(x+n,y+m),get_dis(x-n,y-m)));
printf("%.12f\n",ans);
}
}
gym102900A.Wowoear
一条由\(n\)个线段组成的不自交的折线,你可以选择一条两个端点在折线上但是其他部分不与折线相交的线段,将折线上两端点间的部分替换成这条线段。求操作后折线长度的最小值。
说人话就是你可以抄近路。
举个例子:
大概
\(n\leq 200\)
Hint:调整法考虑最优线段上的端点数(原折线上的)?最优解端点数可能为1吗?
首先就是将这条近路向起点和终点靠近会让他变得更短。
然后如果中间遇到这两种情况:
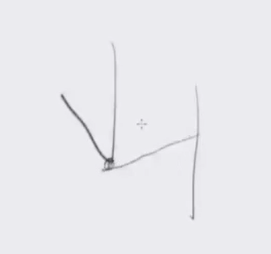

那么若与这条线段有交的原折线的端点数至少有两个,那么这条线段就已经被确定了。
相当于我们可以去枚举沿折线段两个端点然后连一条直线,然后尽量往两个方向延伸。
有一种特殊情况是如果被端点处抄的近路可能会被卡住(有可能可以穿过有可能不可以),\(O(n^2)\)枚举即可。

然后还有可能被一个中间的一个点卡住,可以枚举卡住的点。那么这条线段就相当于是有一个旋转角度,可以对所有的角度分析,把从这个点能看到的折现线段找出来,往两边延伸出线段,找两个交的交点,对于两个交点在折线的线段上移动的时候,考虑三分。
然后各种东西最后时间复杂度为\(O(n^3)\)
不太懂怎么写先贴一份别人的代码之后回来写...
#include<bits/stdc++.h>
using namespace std;
typedef long long s64;
#define rep(i,l,r) for(int i=l;i<=r;++i)
#define per(i,r,l) for(int i=r;i>=l;--i)
template <typename T> void chmin(T &x,const T &y)
{
if(x>y)x=y;
}
typedef long double ld;
int sgn(const ld &x,const ld &eps=1e-9)
{
return x<-eps?-1:x>eps;
}
ld sqr(const ld &x)
{
return x*x;
}
const int N=200+5;
const ld INF=1e9,PI=acos(-1);
struct Point
{
ld x,y;
Point trunc(const ld &len)
{
if(!sgn(x)&&!sgn(y))return {0,0};
ld d=len/sqrt(sqr(x)+sqr(y));
return {x*d,y*d};
}
}p[N];
ld pre[N],suf[N];
ld operator *(const Point &a,const Point &b)
{
return a.x*b.y-b.x*a.y;
}
Point operator -(const Point &a,const Point &b)
{
return {a.x-b.x,a.y-b.y};
}
Point operator +(const Point &a,const Point &b)
{
return {a.x+b.x,a.y+b.y};
}
Point operator *(const Point &a,const ld &b)
{
return {a.x*b,a.y*b};
}
ld dis(const Point &a,const Point &b)
{
return sqrt(sqr(a.x-b.x)+sqr(a.y-b.y));
}
bool in_segment(const Point &a,const Point &p,const Point &q,bool debug=0)
{
return sgn( dis(a,p)+dis(a,q)-dis(p,q),1e-9 ) == 0;
}
ld line_intersection(const Point &a,const Point &b,const Point &p,const Point &q,bool debug=0)
{
ld U=(p-a)*(q-p),D=(b-a)*(q-p);
if(sgn(D,1e-18)==0)return INF;
if( sgn((p-a)*(b-a))*sgn((q-a)*(b-a))>0 )
return INF;
ld t=U/D;
return t;
}
ld check(int i,const Point &pi,int j,const Point &pj)
{
if(i>j)return check(j,pj,i,pi);
//assert(i!=j);
if(pre[i]+dis(p[i],pi)+suf[j]-dis(p[j],pj)+dis(pi,pj)-7.9283<0)
{
//printf("%d %d %f %f %f %f %f\n",i,j,(double)pi.x,(double)pi.y,double(pj.x),double(pj.y),
//double(pre[i]+dis(p[i],pi)+suf[j]-dis(p[j],pj)+dis(pi,pj)));
//printf("%f %f\n", double((pj-pi)*((Point){0,3}-pi)),double((pj-pi)*((Point){0,5}-pi)) );
//exit(0);
}
return pre[i]+dis(p[i],pi)+suf[j]-dis(p[j],pj)+dis(pi,pj);
}
int n;
bool is_valid(const Point &u,const Point &v)
{
rep(i,1,n-1)
{
Point a=p[i],b=p[i+1];
if( sgn((a-u)*(v-u),1e-18)*sgn((b-u)*(v-u),1e-18)<=0 && sgn((u-a)*(b-a),1e-9)*sgn((v-a)*(b-a),1e-9)<0 )
return 0;
}
return 1;
}
int main()
{
#ifdef kcz
freopen("1.in","r",stdin);
#endif
cin>>n;
rep(i,1,n)cin>>p[i].x>>p[i].y;
rep(i,2,n)
{
pre[i]=pre[i-1]+dis(p[i],p[i-1]);
}
per(i,n-1,1)
{
suf[i]=suf[i+1]+dis(p[i],p[i+1]);
}
// rep(i,1,n-1)assert(is_valid(p[i],p[i+1]));
ld ans=pre[n];
rep(i,1,n)
rep(j,i+1,n)
{
ld tl=-INF,tr=INF;
int kl,kr;
rep(k,1,n-1)
if(k!=i&&k+1!=i&&k!=j&&k+1!=j)
{
ld t=line_intersection(p[i],p[j],p[k],p[k+1]);
if(sgn(t-INF)==0)continue;
if(sgn(t)>=0 && sgn(t-1)<=0)continue;
if(sgn(t)<0)
{
if(t>tl)
{
tl=t;kl=k;
}
}
else
{
if(t<tr)
{
tr=t;kr=k;
}
}
}
if(is_valid(p[i],p[j]))
chmin(ans,check(i,p[i],j,p[j]));
Point pl=p[i]+(p[j]-p[i])*tl;
vector<Point>al;
static const ld eps=1e-8;
if(sgn(tl+INF)==0){}
else
{
if(sgn(dis(pl,p[kl+1]))==0)++kl;
int dl=sgn(dis(pl,p[kl]))==0;
if(kl-dl>0)al.push_back(pl + (p[kl-dl]-pl).trunc(eps));
if(kl<n)al.push_back(pl + (p[kl+1]-pl).trunc(eps));
for(auto p1:al)
if(is_valid(p1,p[j]))
{
chmin(ans,check(kl,pl,j,p[j]));
break;
}
al.push_back(pl);
}
Point pr=p[i]+(p[j]-p[i])*tr;
vector<Point>ar;
if(sgn(tr-INF)==0){}
else
{
if(sgn(dis(pr,p[kr+1]))==0)++kr;
int dr=sgn(dis(pr,p[kr]))==0;
if(kr-dr>0)ar.push_back(pr + (p[kr-dr]-pr).trunc(eps));
if(kr<n)ar.push_back(pr + (p[kr+1]-pr).trunc(eps));
for(auto p1:ar)
if(is_valid(p1,p[i]))
{
chmin(ans,check(kr,pr,i,p[i]));
break;
}
ar.push_back(pr);
}
for(auto p1:al)
for(auto p2:ar)
if(is_valid(p1,p2))
{
chmin(ans,check(kl,pl,kr,pr));
goto End;
}
End:;
}
rep(k,2,n-1)
{
vector<ld>a;
rep(i,1,n)
if(i!=k)
{
Point np=p[i]-p[k];
ld t=atan2(np.y,np.x);
a.push_back((t<=-PI/2)?-PI/2-t:( t<=PI/2?PI/2-t:PI/2+(PI-t) ));
}
a.push_back(0);a.push_back(PI);//a.push_back(PI/2);
sort(a.begin(),a.end());
int sz=a.size();
rep(i,0,sz-2)
{
ld l=a[i],r=a[i+1];
if(sgn(r-l)==0)continue;
ld m=(l+r)/2;
ld m1=PI/2-m;
Point p1=p[k]+(Point){cos(m1),sin(m1)};
ld tl=-INF,tr=INF;
int kl,kr;
rep(i,1,n-1)
if(i!=k&&i+1!=k)
{
ld t=line_intersection(p[k],p1,p[i],p[i+1]);
if(!sgn(t-INF))continue;
if(t<0)
{
if(t>tl)
{
tl=t;kl=i;
}
}
else
{
if(t<tr)
{
tr=t;kr=i;
}
}
}
if(!sgn(tl+INF)||!sgn(tr-INF))continue;
Point pl=p[k]+(p1-p[k])*tl,pr=p[k]+(p1-p[k])*tr;
if(sgn( (pr-pl)*(p[k+1]-pl) )*sgn( (pr-pl)*(p[k-1]-pl) )<0 )
continue;
auto F=[&](const ld &m)
{
ld m1=PI/2-m;
Point p1=p[k]+(Point){cos(m1),sin(m1)};
ld tl=line_intersection(p[k],p1,p[kl],p[kl+1],k==3 && kl==1 &&kr==9);
Point pl=p[k]+(p1-p[k])*tl;
ld tr=line_intersection(p[k],p1,p[kr],p[kr+1]);
Point pr=p[k]+(p1-p[k])*tr;
return check(kl,pl,kr,pr);
};
rep(tmp,0,100)
{
ld m1=(l*2+r)/3,m2=(l+r*2)/3;
if(F(m1)<F(m2))r=m2;
else l=m1;
}
chmin(ans,F(l));
}
}
printf("%.9f\n",(double)ans);
}
gym102900H.Rice Arrangement
有两组\(k\)个\([0,n)\)间的整数,称为\(a\)和\(b\)。将他们两两匹配,并为每对分配整数\(c\)使得\(((a+c)\bmod n)=b\),最小化\((\max(0,\max c)-\min (0,\min c))\)。
\(n\leq 10^9,k\leq 5\times 10^3\)
Hint:将匹配考虑成圆环上的有向线段,可以推出什么性质?能否破环为链?请给出证明。
比如现在有\(a=\{1,8\},b=\{2,7\}\),那么最优的匹配就是\(1\to 2,c=1\)以及\(8\to 7,c=-1\),最后答案就是\(2\)。
考虑写在圆环上:

然后可以发现两条线段不可能方向相反的相交:

因为这样可以调整成这个样子,使两个有向线段变得更短:
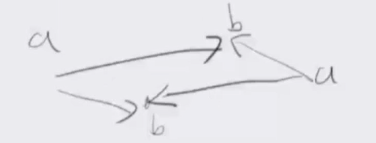
然后来考虑是否能断环成链:
还有一个性质是一个方向的有向线段的并一定不可能是整个圆:
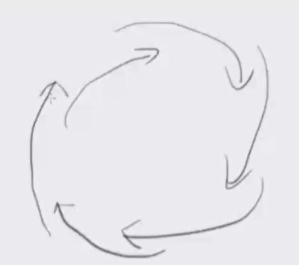
考虑反证,假设它把整个圆覆盖了,那么令每条线段的左端点单调上升,这样一定可以每个点都匹配到接近的,即将一圈的线段都缩短:

而又因为两条线段不可能方向相反的相交,所以在圆上一定可以找到一个点然后它不被任意一条有向线段覆盖。
那么就可以由这个点将整个圆剖开,这样的话所有的有向线段就都在这个数轴上了,那么就可以贪心的从左到右匹配了(最左边的点一定匹配较左边的点)。
这样我们可以直接枚举第一个人选择哪个,然后转一圈计算答案。复杂度\(O(n^2\log n)\)
不过好像也可以\(O(n^2)\)。
int n,k;
int a[11111],b[11111];
signed main()
{
for(int _=read();_;_--)
{
n=read(),k=read();
R(i,0,k-1) a[i]=read();
R(i,0,k-1) b[i]=read();
sort(a,a+k),sort(b,b+k);
int ans=n;
R(x,0,k-1)
{
vector<int>c={0,n};
R(i,0,k-1) c.pb((a[i]-b[(i+x)%k]+n)%n);
sort(c.begin(),c.end());
R(i,0,k) ckmin(ans,n-(c[i+1]-c[i])+min(c[i],n-c[i+1]));
}
writeln(ans);
}
}
gym102900K.Traveling Merchant
\(n\)个点\(m\)条边⽆向图,给定每个点⿊⾊或⽩点。从⼀个点离开时会翻转这个点的颜⾊,判断是否存在从⼀号点出发的⽆限⻓的⿊⽩相间的路径。
\(1\leq n,m\leq 2\times 10^5\)
Hint 1:点双联通分量满足任意三个点\(x,y,z\),存在一条\(x\to y\to z\)的简单路径。(why?)
Hint 2:考虑最⼤流最⼩割定理。还能得到点双的什么性质?
走的路径若是无限长就一定会走重复的点,然后考虑第一个走重复的点,则一定形成了一个简单环。
且这个环长度一定是奇数,且是黑白相间的。
所以说找一个黑白相间且形成一个奇环与存在一条无限长的黑白相间的路径是等价的。
所以考虑把黑白点分到两个集合,看成一个二分图,每次走二分图之间的边,为了形成奇环走到一个同色的点。
大概长这个样子:
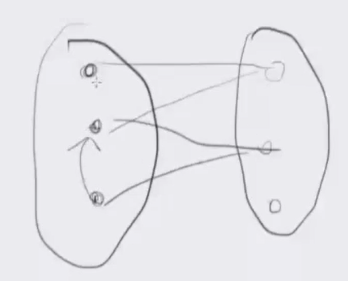
那么现在需要判断在二分图内,对于每一条同色边\((u,v)\),判断是否存在一条\(1\to u \to v\)或者\(1\to v \to u\)的简单路径。注意必须是简单路径,不然就不是第一个重复的点。
考虑先对无向图证明这个东西:
考虑如果是\(x\to y\to z\)的简单路径
可以从\(y\)这个点建一个建一个有流量限制的网络流,给\(y\)一个流量\(2\),\(x,z\)一个流量\(1\)。对于其中每一个点流量限制为\(1\),如果最大流是\(2\)就行了。
具体原因为由于最大流最小割定理,中间的边都可以设为\(+\infty\)。若最大流为\(1\)则说明存在一个最小割为\(1\),即存在一个点,将它去掉之后能将\(y\)和\(x,z\)分开,这就不对了。所以最大流为\(2\)。

然后对于本题:
对于任意一张有向图判断是否存在\(1\to y\to z\)的简单有向路径,考虑1的dfs树,考虑\(y\)和\(z\):
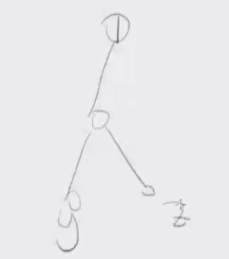
若\(y\)和\(z\)有祖先关系就直接做完了,否则考虑在圆方树上找出\(y\)的双连通分量,从\(1\)号点沿圆方树走到\(y\)这个双连通分量的第一个点,以及从\(y\)这个双连通分量走出去走到\(z\)的双连通分量的第一个点。这三个点一定存在简单有向路径只需要考虑\(1\to x'\)与\(z'\to z\)是否存在交即可。
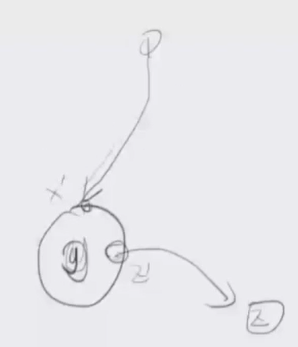
所以直接在dfs树上找\(y\)和\(z\)的LCA,然后判与\(y\)和\(z\)是否在同一个点双连通分量即可。
int n;
int a[888888][6];
int szx,szy,szz;
vector<int>vec[3];
vector<pair<pair<ll,ll>,pair<ll,ll> > >t[888888];
void add_t(int L,int R,int l,int r,int x,const pair<pii,pii> &k)
{
if(L<=l&&r<=R) {t[x].pb(k);return;}
int mid=(l+r)>>1;
if(L<=mid) add_t(L,R,l,mid,x<<1,k);
if(mid<R) add_t(L,R,mid+1,r,x<<1|1,k);
}
int tot_seg,pre[888888];
int del[888888];
int mn1[888888],mx1[888888],tag1[888888];
int mn2[888888],mx2[888888],tag2[888888];
int sdel[888888];
int smn1[888888],smx1[888888],stag1[888888];
int smn2[888888],smx2[888888],stag2[888888];
inline void print(int x)
{
puts("");
puts("----------------asdasdsa---------------");
printf("x:%lld\n",x);
R(i,1,10) printf("del:%lld mn1:%lld mx1:%lld tag1:%lld mn2:%lld mx2:%lld tag2:%lld\n",del[i],mn1[i],mx1[i],tag1[i],mn2[i],mx2[i],tag2[i]);
puts("----------------bsadasds---------------");
puts("");
}
void build(int l,int r,int x)
{
del[x]=mn2[x]=mx2[x]=szy+1;
if(l==r) return;
int mid=(l+r)>>1;
build(l,mid,x<<1),build(mid+1,r,x<<1|1);
}
void mkns(int x)
{
pre[++tot_seg]=x;
sdel[tot_seg]=del[x];
smn1[tot_seg]=mn1[x],smx1[tot_seg]=mx1[x],stag1[tot_seg]=tag1[x];
smn2[tot_seg]=mn2[x],smx2[tot_seg]=mx2[x],stag2[tot_seg]=tag2[x];
}
void dels(int x)
{
static int F;
for(;tot_seg!=x;)
{
F=pre[tot_seg];
del[F]=sdel[tot_seg];
mn1[F]=smn1[tot_seg],mx1[F]=smx1[tot_seg],tag1[F]=stag1[tot_seg];
mn2[F]=smn2[tot_seg],mx2[F]=smx2[tot_seg],tag2[F]=stag2[tot_seg];
tot_seg--;
}
}
void upd1(int x,int k)
{
mkns(x);
mn1[x]=mx1[x]=tag1[x]=k;
del[x]=mx2[x]-k;
}
void upd2(int x,int k)
{
mkns(x);
mn2[x]=mx2[x]=tag2[x]=k;
del[x]=k-mn1[x];
}
void push_down(int x)
{
if(!tag1[x]&&!tag2[x]) return;
mkns(x);
if(tag1[x])
{
upd1(x<<1,tag1[x]);
upd1(x<<1|1,tag1[x]);
tag1[x]=0;
}
if(tag2[x])
{
upd2(x<<1,tag2[x]);
upd2(x<<1|1,tag2[x]);
tag2[x]=0;
}
}
void push_up(int x)
{
del[x]=max(del[x<<1],del[x<<1|1]);
mx1[x]=max(mx1[x<<1],mx1[x<<1|1]);
mx2[x]=max(mx2[x<<1],mx2[x<<1|1]);
mn1[x]=min(mn1[x<<1],mn1[x<<1|1]);
mn2[x]=min(mn2[x<<1],mn2[x<<1|1]);
}
void modify1(int L,int R,int l,int r,int x,int k)
{
if(mn1[x]>=k) return;
if(L<=l&&r<=R&&mx1[x]<=k)
{
upd1(x,k);
return;
}
push_down(x);
int mid=(l+r)>>1;
if(L<=mid) modify1(L,R,l,mid,x<<1,k);
if(mid<R) modify1(L,R,mid+1,r,x<<1|1,k);
mkns(x);
push_up(x);
}
void modify2(int L,int R,int l,int r,int x,int k)
{
if(mx2[x]<=k) return;
if(L<=l&&r<=R&&mn2[x]>=k)
{
upd2(x,k);
return;
}
push_down(x);
int mid=(l+r)>>1;
if(L<=mid) modify2(L,R,l,mid,x<<1,k);
if(mid<R) modify2(L,R,mid+1,r,x<<1|1,k);
mkns(x);
push_up(x);
}
void query(int l,int r,int x,int posz)
{
if(l==r)
{
puts("YES");
printf("%lld %lld %lld\n",vec[0][l-1],vec[1][max(mn1[x]-1,0ll)],vec[2][posz-1]);
exit(0);
}
push_down(x);
int mid=(l+r)>>1;
if(del[x<<1]>=0) query(l,mid,x<<1,posz);
else query(mid+1,r,x<<1|1,posz);
}
void solve(int l,int r,int x)
{
int df=tot_seg;
static int lx,rx,ly,ry;
//printf("siz:%lld\n",(int)t[x].size());
// print(-1);
for(auto qwq:t[x])
{
// print(0);
lx=qwq.fi.fi,rx=qwq.fi.se,ly=qwq.se.fi,ry=qwq.se.se;
if(lx>1) modify1(1,lx-1,1,szx,1,ly);
// print(1);
if(rx<szx) modify1(rx+1,szx,1,szx,1,ly);
// print(2);
if(lx>1) modify2(1,lx-1,1,szx,1,ry);
// print(3);
if(rx<szx) modify2(rx+1,szx,1,szx,1,ry);
// print(4);
}
if(l==r)
{
if(del[1]>=0) query(1,szx,1,l);
}
else
{
int mid=(l+r)>>1;
solve(l,mid,x<<1),solve(mid+1,r,x<<1|1);
}
dels(df);
}
signed main()
{
n=read();
R(i,1,n) R(j,0,5) a[i][j]=read(),vec[j>>1].pb(a[i][j]+(j&1));
R(i,0,2) sort(vec[i].begin(),vec[i].end()),vec[i].erase(unique(vec[i].begin(),vec[i].end()),vec[i].end());
R(i,1,n) R(j,0,5) a[i][j]=lower_bound(vec[j>>1].begin(),vec[j>>1].end(),a[i][j]+(j&1))-vec[j>>1].begin()+1-(j&1);
szx=(int)vec[0].size()-1,szy=(int)vec[1].size()-1,szz=(int)vec[2].size()-1;
R(i,1,n)
{
if(a[i][4]>1)
add_t(1,a[i][4]-1,1,szz,1,mkp(mkp(a[i][0],a[i][1]),mkp(a[i][2],a[i][3])));
if(a[i][5]<szz)
add_t(a[i][5]+1,szz,1,szz,1,mkp(mkp(a[i][0],a[i][1]),mkp(a[i][2],a[i][3])));
}
build(1,szx,1);
solve(1,szz,1);
puts("NO");
}
gym102900J.Octasaction
给定\(n\)个三维⽴⽅体\((x0,y0,z0)-(x1,y1,z1)\) 判断是否存在三个平⾯\(x=a,y=b,z=c\)使得每个⽴⽅体都和⾄少⼀个平⾯有交。
\(n\leq 10^5\)
Hint 1:考虑立方体对解\((a,b,c)\)的限制。(类比二维情况,可以枚举一维)。
Hint 2:枚举一维后对时间使用线段树trick使操作变为add和rollback,如何快速判断十字形的交非空?(考虑补集的并?)
比如扫描一个平面,一个限制被删除的时间段是一个区间,可以在一个对时间建的线段树上把区间分成\(\log\)段,然后把它放进去。线段树的每一个叶子节点都表示一个时刻,当要找到某一个时刻的限制只需要从线段树的根走到叶子节点,把它上面那些限制加上就行了。
考虑直接枚举一维
问题可以转化成\(x\in[x_{0i},x_{1i}]\or y\in [y_{0i},y_{1i}]\),它的解集就长成一个十字形状。
然后需要对于这些十字形求交,然后判断交是否非空。
考虑反面问题,它们补集的并是否是全集。
它们的补集由4块长方形并起来,然后考虑去维护它们的轮廓。它由两边并起来,所以一定是一个单峰函数。

然后我们需要判一段轮廓线是否存在空隙,这就是一组解。
考虑维护区间上轮廓最大值,下轮廓最小值,以及区间的一组解(或没有)。
然后反正各种修改,合并。
大致思路就这样,时间复杂度\(O(n\log ^2 n)\)
int n;
int a[111111][6];
int szx,szy,szz;
vector<int>vec[3];
vector<pair<pii,pii> >t[444444];
void add_t(int L,int R,int l,int r,int x,const pair<pii,pii> &k)
{
if(L<=l&&r<=R) {t[x].pb(k);return;}
int mid=(l+r)>>1;
if(L<=mid) add_t(L,R,l,mid,x<<1,k);
if(mid<R) add_t(L,R,mid+1,r,x<<1|1,k);
}
int tot_seg,pre[444444];
int del[444444];
int mn1[444444],mx1[444444],tag1[444444];
int mn2[444444],mx2[444444],tag2[444444];
int sdel[444444];
int smn1[444444],smx1[444444],stag1[444444];
int smn2[444444],smx2[444444],stag2[444444];
void build(int l,int r,int x)
{
del[x]=mn2[x]=mx2[x]=szy+1;
if(l==r) return;
int mid=(l+r)>>1;
build(l,mid,x<<1),build(mid+1,r,x<<1|1);
}
void mkns(int x)
{
pre[++tot_seg]=x;
sdel[tot_seg]=sdel[x];
smn1[tot_seg]=mn1[x],smx1[tot_seg]=mx1[x],stag1[tot_seg]=tag1[x];
smn2[tot_seg]=mn2[x],smx2[tot_seg]=mx2[x],stag2[tot_seg]=tag2[x];
}
void dels(int x)
{
static int F;
for(;tot_seg^x;tot_seg--)
{
F=pre[tot_seg];
del[F]=sdel[tot_seg];
mn1[F]=smn1[tot_seg],mx1[F]=smx1[tot_seg],tag1[F]=stag1[tot_seg];
mn2[F]=smn2[tot_seg],mx2[F]=smx2[tot_seg],tag2[F]=stag2[tot_seg];
}
}
void upd1(int x,int k)
{
mkns(x);
mn1[x]=mx1[x]=tag1[x]=k;
del[x]=mx2[x]-k;
}
void upd2(int x,int k)
{
mkns(x);
mn2[x]=mx2[x]=tag2[x]=k;
del[x]=k-mn1[x];
}
void push_down(int x)
{
if(!tag1[x]&&!tag2[x]) return;
mkns(x);
if(tag1[x])
{
upd1(x<<1,tag1[x]);
upd1(x<<1|1,tag1[x]);
tag1[x]=0;
}
if(tag2[x])
{
upd2(x<<1,tag2[x]);
upd2(x<<1|1,tag2[x]);
tag2[x]=0;
}
}
void push_up(int x)
{
del[x]=max(del[x<<1],del[x<<1|1]);
mx1[x]=max(mx1[x<<1],mx1[x<<1|1]);
mx2[x]=max(mx2[x<<1],mx2[x<<1|1]);
mn1[x]=min(mn1[x<<1],mn1[x<<1|1]);
mn2[x]=min(mn2[x<<1],mn2[x<<1|1]);
}
void modify1(int L,int R,int l,int r,int x,int k)
{
if(mn1[x]>=k) return;
if(L<=l&&r<=R&&mx1[x]<=k)
{
upd1(x,k);
return;
}
push_down(x);
int mid=(l+r)>>1;
if(L<=mid) modify1(L,R,l,mid,x<<1,k);
if(mid<R) modify1(L,R,mid+1,r,x<<1|1,k);
mkns(x);
push_up(x);
}
void modify2(int L,int R,int l,int r,int x,int k)
{
if(mx2[x]<=k) return;
if(L<=l&&r<=R&&mn2[x]>=k)
{
upd2(x,k);;
return;
}
push_down(x);
int mid=(l+r)>>1;
if(L<=mid) modify2(L,R,l,mid,x<<1,k);
if(mid<R) modify2(L,R,mid+1,r,x<<1|1,k);
mkns(x);
push_up(x);
}
void query(int l,int r,int x,int posz)
{
if(l==r)
{
puts("YES");
printf("%lld %lld %lld\n",vec[0][l-1],vec[1][max(mn1[x]-1,0ll)],vec[2][posz-1]);
exit(0);
}
push_down(x);
int mid=(l+r)>>1;
if(del[x<<1]>=0) query(l,mid,x<<1,posz);
else query(mid+1,r,x<<1|1,posz);
}
void solve(int l,int r,int x)
{
int df=tot_seg;
static int lx,rx,ly,ry;
for(auto qwq:t[x])
{
lx=qwq.fi.fi,rx=qwq.fi.se,ly=qwq.se.fi,ry=qwq.se.se;
if(lx>1) modify1(1,lx-1,1,szx,1,ly),modify2(1,lx-1,1,szx,1,ry);
if(rx<szx) modify1(rx+1,szx,1,szx,1,ly),modify2(rx+1,szx,1,szx,1,ry);
}
if(l==r)
{
if(del[1]>=0) query(1,szx,1,l);
dels(df);
return;
}
int mid=(l+r)>>1;
solve(l,mid,x<<1),solve(mid+1,r,x<<1|1);
dels(df);
}
signed main()
{
n=read();
R(i,1,n) R(j,0,5) a[i][j]=read(),vec[j>>1].pb(a[i][j]+(j&1));
R(j,0,2) sort(vec[j].begin(),vec[j].end()),vec[j].erase(unique(vec[j].begin(),vec[j].end()),vec[j].end());
R(i,1,n) R(j,0,5) a[i][j]=lower_bound(vec[j>>1].begin(),vec[j>>1].end(),a[i][j]+(j&1))-vec[j>>1].begin()+1-(j&1);
szx=(int)vec[0].size()-1,szy=(int)vec[1].size()-1,szz=(int)vec[2].size()-1;
R(i,1,n)
{
if(a[i][4]>1)
add_t(1,a[i][4]-1,1,szz,1,mkp(mkp(a[i][0],a[i][1]),mkp(a[i][2],a[i][3])));
if(a[i][5]<szz)
add_t(a[i][5]+1,szz,1,szz,1,mkp(mkp(a[i][0],a[i][1]),mkp(a[i][2],a[i][3])));
}
build(1,szx,1);
solve(1,szz,1);
puts("NO");
}
2020ICPC⼩⽶邀请赛决赛
https://ac.nowcoder.com/acm/contest/9328
J. Rikka with book
给定\(n\)块木板的宽度及质量,将他们叠起来放在桌边,求稳定状态下从桌边延伸出的最长长度。
\(n\leq 20\)。
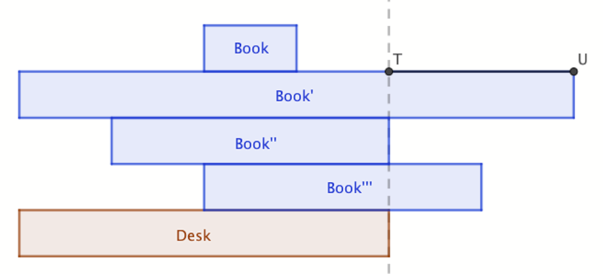
Hint 0:稳定条件为对于每个⽀撑⾯,⽀撑物的重⼼落在⽀撑⾯内。
Hint 1:⽤贡献答案的书分为上下两部分,下部分重⼼⼀定最靠右。平衡条件和答案的贡献可以独⽴算吗?
令\(c_i\)表示前\(i\)个木板的重心,而往右延长的长度为重心之前的差\(c_i-c_{i+1}\)。然后先来考虑下面那部分,发现每一层重心之差是独立的在最大化这个东西。然后以最长的作为分界线,下面的重心一定在最右边,而上面只跟压住它的重心和质量有关,那么这一定是在他的最左边压住他。
具体考虑状压,令\(dp[S]\)表示一个集合里面的书的重心可以延伸出桌子多少距离。然后可以由\(S\)转移到\(S\)的子集,每次枚举一个木板把他放到最底下,考虑重心的偏移量,\(dp\)最大化这个东西。最后对于每一个\(dp[S]\),在\(S\)集合中枚举一个让他伸得最远,然后把剩下的书压在他身上,看能比重心伸长多少,大概就是\(\max\{dp[S]+ ...\}\)。
时间复杂度\(O(2^n\times n)\)
double v[22],l[22];
double dp[1<<22];
int n;
signed main()
{
ios::sync_with_stdio(false);
cin>>n;
R(i,0,n-1) cin>>l[i];
R(i,0,n-1) cin>>v[i];
R(mask,1,(1<<n)-1)
{
double sum=0;
R(i,0,n-1) if(mask&(1<<i)) sum+=v[i];
R(i,0,n-1) if(mask&(1<<i))
{
ckmax(dp[mask],dp[mask^(1<<i)]+v[i]/sum*l[i]/2);
ckmax(dp[mask],l[i]-v[i]/sum*l[i]/2);
}
}
printf("%.10f\n",dp[(1<<n)-1]);
}
M. Rikka with employees
给定一棵\(n\)个节点的树。你有一个栈,可以进行将未入栈的一个节点压栈、弹栈两种操作。使用不超过\(9\times 10^6\)次操作,使得对于每个节点\(x\)都在某个时刻出现过这样的状态:有且仅有\(x\)的子树节点未入栈。(注意这里是一个栈的结构!)
\(n\leq 10^5\)。
Hint 1:菊花图?链?
Hint 2:按照重链分治?
关于操作次数复杂度:
构建若干个\(size\)和为\(n\)的线段的线段树,如果使线段树上总线段长度为\(O(n\log n)\)?
先考虑怎么做菊花图
设\(\operatorname{solve(l,r)}\)为调用这个函数前只有\([l,r]\)不在栈中,在过程中将\(S(l),S(l+1),\ldots S(r)\)都完成,并且结束之后又回到\([l,r]\)不在栈中的状态。
然后令\(m=\frac{l+r}{2}\),先将\([m+1,r]\)都加入栈中,然后\(\operatorname{solve(l,mid)}\),再将\([m+1,r]\)全部删掉,再加入左边,最后再\(\operatorname{solve(m+1,r)}\),最后删除左边。
然后考虑推广到一般情况:
但是由于可能深度很深所以并不能直接这样递归下去。
考虑按照重链分治,每次找一个重链,每次重链上都挂着几棵子树。
与刚刚的递归过程类似,先把重链放进去,这样剩下的子树就回到了刚刚菊花图的情况,虽然它们并不是连在同一个点上,但是除了它们以外的点已经在栈里了,所以就可以用之前菊花图的分治方法去做。
对于每一棵小子树,我们现在就是把其他所有子树填满之后就递归下去。
对于重链上的点就是依次填满,然后回溯的时候弹掉。
这样就相当于把树里所有点的状态都到达了一遍。
需要注意这两个过程都与节点个数相关,即分治的时候不应该按照树的个数分治,应该按照节点大小分治,即假设将\(n\)个节点分成\(a_1,a_2,\ldots a_n\)大小的小子树,那么在做菊花图分治时应该将\(\sum \limits_{i=1}^m a_i\)与\(\sum\limits_{i=m+1}^n a_i\)之差尽量小。
inline void f1(int x){printf("+%d",x);}
inline void f2(){printf("-");}
inline void f3(int x){printf("=%d",x);}
int n;
vector<int>e[222222];
int fa[222222];
int siz[222222],hson[222222];
void dfs1(int u)
{
siz[u]=1;
for(int v:e[u])
{
dfs1(v);
siz[u]+=siz[v];
if(siz[hson[u]]<siz[v]) hson[u]=v;
}
}
inline void add_subt(int u)
{
f1(u);for(int v:e[u]) add_subt(v);
}
inline void del_subt(int u)
{
f2();for(int v:e[u]) del_subt(v);
}
void dfs2(int u);
void solve(const vector<int>&sons)
{
if((int)sons.size()==1) return dfs2(sons.back());
vector<int>l,r;
int sum=0,tmp=0;
for(int u:sons) sum+=siz[u];
for(int u:sons)
{
if(tmp+siz[u]>sum/2) r.pb(u);
else l.pb(u),tmp+=siz[u];
}
for(int u:r) add_subt(u);
solve(l);
for(int u:r) del_subt(u);
for(int u:l) add_subt(u);
solve(r);
for(int u:l) del_subt(u);
}
void dfs2(int u)
{
vector<int>hchain,sons;
for(int cur=u;cur;cur=hson[cur]) hchain.pb(cur);
for(int u:hchain)
{
f3(u),f1(u);
for(int v:e[u]) if(v!=hson[u])
{
add_subt(v);
sons.pb(v);
}
}
R(i,1,siz[u]) f2();
for(int u:hchain) f1(u);
sort(sons.begin(),sons.end(),[&](int x,int y){return siz[x]<siz[y];});
if((int)sons.size()) solve(sons);
for(int u:hchain) f2();
}
signed main()
{
n=read();
R(i,2,n) fa[i]=read(),e[fa[i]].pb(i);
dfs1(1);
dfs2(1);
puts("!");
}
L. Rikka with generals
给定\(n\)个节点的树,每个节点初始有⼀个数字,这些数字形成⼀个\(n\)的排列。每次操作可以交换树上相邻的且数字相邻的数字。求初始状态可以到达的不同状态数,答案对\(998244353\)取模。
\(n\leq 2\times 10^5\)
Hint:⼀个数字只需要关⼼与它相邻的两个数字的位置,且相邻的数字⾄多只需要交换⼀次。能否按照数字从小到大动态规划?
考虑加上一个限制只能与某个相邻的数交换一次,那么这也是可以到达所有可能到达的状态。
所以相邻的\(x\)和\(x-1\)交换之后,\(x\)与\(x-1\)不能再次交换,因此在交换之后\(x-1\)只能和\(x-2\)交换,\(x\)只能和\(x+1\)交换,然后若\(x-1\)再和\(x-2\)交换,那么\(x-1\)就再也动不了了。
因此一个\(x\)在最终可能的状态中,一定在距离原来的点\(\leq 2\)上。
所以对于\(1\sim n\)的每个\(x\),求出交换路径。即确定了\(1\sim x\)的交换路径,再考虑到\(x+1\sim n\)需要记录什么。发现\(1\sim x-1\)都是在内部交换的,只有\(x\)号点会和\(x+1\)交换,所以只需要关心这个东西就行了。
那么需不需要关心它会不会占用别的点的位置呢?并不需要,因为我们并不是关心哪些点被占用了,我们只关心相邻的点在哪:比如说对于\(x+1\),我们只关心\(x\)和\(x+2\)在哪,所以只要知道\(x\)用了哪条边与\(x+1\)交换。
所以设状态为\(f(x,e)\)其中\(e\)为\(\varnothing\)或一条有向边,表示\(x\)号点在\(e\)号边与\(x+1\)交换。
然后就可以进行转移了,每个枚举是先跟\(x-1\)交换还是先跟\(x+1\)进行交换,然后如果由之前的状态转移而来就看一下它们是不是真的在这里进行了交换。
但是这样状态数看起来很大,考虑优化。
当\(x\)要跟\(x+1\)进行交换的时候,可以发现一定是确定有一条边的,因此只要看\(x+1\)点在\(x\)的哪一个子树内就行了。因为\(x+1\)号点最多只能走两步,并且在于\(x\)号点交换之前只能走一步,所以它不可能从一个子树跑到另一棵子树。因此只用考虑\(x+1\)号点的原位置在\(x\)号点的哪个子树内然后去交换。
因此转移总个数就是对于每个点看它要不要先走到邻居上(与\(x-1\)号点进行交换),然后再看要不要与\(x+1\)号点进行交换。
因此时间复杂度为\(O\left(\sum \deg_i\right)=O(n)\)。
int n;
int p[222222],pos[222222];
vector<int>e[222222];
int L[222222],R[222222];
int cc[222222],f1[222222],f2[222222];
int pre[222222];
signed main()
{
for(int _=read();_;_--)
{
n=read();
R(i,0,n+5) e[i].clear(),f1[i]=f2[i]=cc[i]=pos[i]=0,pre[i]=-1;
int u,v;
R(i,2,n) u=read(),v=read(),e[u].pb(v),e[v].pb(u);
R(i,1,n) p[i]=read(),pos[p[i]]=i;
int lst=-1;
R(i,1,n-1)
{
static int vis[222222];
u=pos[i],v=pos[i+1];
for(int x:e[v]) vis[x]=1;
if(vis[u])
{
cc[i]=1;
for(L[i]=i;L[i]>1&&vis[pos[L[i]-1]];L[i]--);
if(~lst&&L[i]==R[lst]+1&&vis[pos[lst]]) pre[i]=lst;
for(int x:e[v]) vis[x]=0;
for(int x:e[u]) vis[x]=1;
for(R[i]=i+1;R[i]+1<=n&&vis[pos[R[i]+1]];R[i]++);
for(int x:e[u]) vis[x]=0;
lst=i;
}
else for(int x:e[v]) vis[x]=0;
}
f1[1]=1;
R(i,1,n)
{
f1[i+1]+=f1[i],f1[i+1]%=mod;
if(cc[i])
{
if(~pre[i]) f2[i]=f2[pre[i]];
R(j,L[i],i) f2[i]+=f1[j],f2[i]%=mod;
R(j,i+2,R[i]+1) f1[j]+=f2[i],f1[j]%=mod;
}
}
writeln(f1[n+1]);
}
}
C. Rikka with Random tree
咕
A. Rikka with Game
\(n\)个⼈玩游戏,给定所有⼈都知道的双向朋友关系。游戏⼀开始某⼈被选为恶⻰,进⾏若⼲轮:
- 每轮⼀开始所有⾮⻰玩家独⽴决定是否屠⻰,但是与⻰玩家为朋友的玩家不会屠⻰
- ⻰玩家会被编号最⼩的屠⻰玩家杀死,下⼀轮该屠⻰玩家成为⻰。若⽆屠⻰,则游戏结束。
游戏结束后,活着的⻰玩家获得\(100\)分,活着的⾮⻰玩家获得\(10\)分,死掉的玩家获得\(1\)分。对于每个\(i\),求第\(i\)个玩家初始被选为⻰时游戏是否会在第⼀轮结束。每个⼈仅最⼤化⾃⼰的得分。
\(n\leq 500\)
Hint 1:
最优策略下,屠⻰者成⻰后⼀定不会被杀。在同时做决定是否屠⻰的阶段时,屠⻰与否⼀定会改变⾃⼰的最终收益,所以在多个⼈屠⻰的局⾯被避免后最优策略唯⼀,且可以视为编号从⼩到⼤依次做决定。
因此这个游戏并不会超过两轮,因为杀龙的人一定不会被杀。
Hint 2:
⼀个局⾯⼀个⼈当⻰没被杀当且仅当所有能杀他的⼈杀了他之后都会被杀。(被杀:没被杀的反命题)
设\(P(x)\)为某个局⾯当⻰的⼈是否没被杀。\(P(x)\)为真当且仅当所有\(P(y)\)为假(\(y\)是\(x\)可转移的状态)
终⽌条件?⽆可转移状态\(P(x)=true\)
考虑相似的博弈模型…?
所有状态及转移形成一个DAG,两个人在DAG上进行博弈\([P(x)=true]\)当且仅当所有\([P(y)=false]\)。
[当前状态是失败态]当且仅当所有[转移都是胜利态]
\(P(x)=\) 状态\(x\)是否是失败态
考虑朋友关系的补图,初始第\(x\)个人成龙没被杀可以被转化为:一个棋子初始被放在\(x\)号点,两个人轮流将棋子移动到相邻的之前没放过的点,不能移动则输。龙没被杀等价于该初始状态为失败态。
Hint 3:
考虑朋友关系补图的最大匹配、增广路
经典博弈论模型结论:后手必胜当且仅当存在不包含\(x\)点的最大匹配。
假设存在不包含\(x\)点的最大匹配,那么先手每步都会走到一个匹配点上,否则将会存在一个增广路径。所以后手每步都一定可以走匹配边。
逆否命题?
所有最大匹配都包含\(x\)点,那么不存在一条从\(x\)点出发到一个未匹配点的交错路径,所以先手每步从匹配边一定必胜。
然后就变成相当于判断存不存在一个不包含某个点的最大匹配。
具体做法为先求出任意一个最大匹配(带花树),然后对于那些匹配的点找存不存在一条交错路径(判断是否不在最大匹配中)。
B. Rikka with Maximum Segment sum
咕


 浙公网安备 33010602011771号
浙公网安备 33010602011771号