图论和网络流相关
强连通分量(scc)
在有向图\(G\)中,若两个顶点\(u,v\)之间能够互相到达,则称\(u,v\)是强连通的。若有向图\(G\)的每两个顶点都强连通,则\(G\)就是一个强连通图。
有向图的极大强连通子图,称作强连通分量。
强连通缩点
将一个图中的每一个强连通分量都缩成一个点的过程,称为强连通缩点。容易发现。缩点后的图一定是个DAG。
强连通缩点可以由Kosaraju算法或者Tarjan算法(似乎还有一种)
下面稍微讲一下Kosaraju算法
Kosaraju
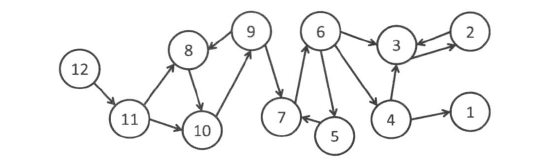
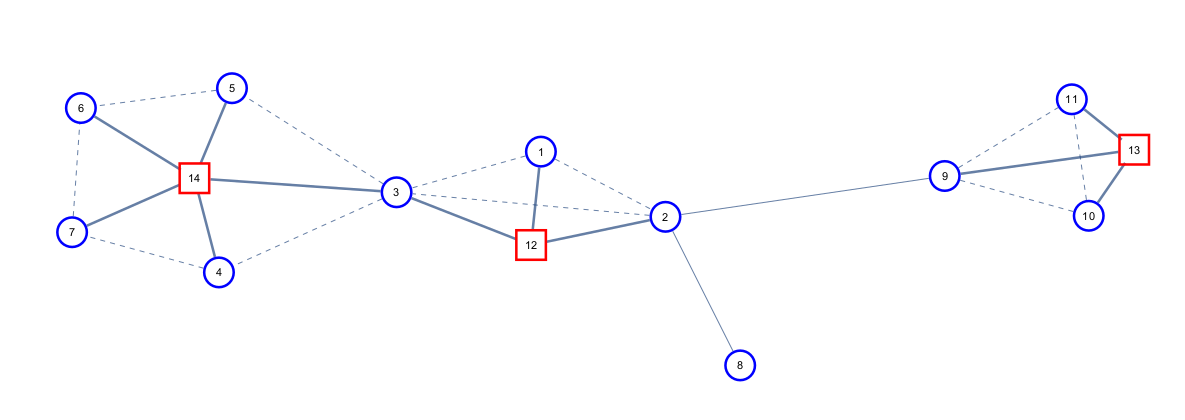
先跑一遍,记录它的posorder,也就是它的返回顺序。
如对于上面这张图从12开始dfs,它的posorder就是\(1,2,\ldots ,12\)
以及在DAG中,posorder是拓扑序的反序。
在记录这个的posorder后,将这个图的边反向。
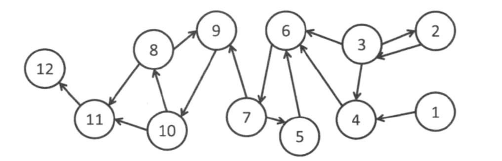
从最后一个点开始(还是12)在反向图上跑一遍dfs,然后每一次dfs就访问一些点,可以发现这一些点就是一个强连通分量。
大概是因为posorder是DAG的拓扑序列的逆序,将原图的边反向之后,所以最终第二遍dfs的顺序其实就是缩点之后DAG的拓扑序。
例题1
https://codeforces.ml/contest/949/problem/C
阅读理解题
题意
\(n\)个点,每个点\(i\)有一个值\(a_i\)。\(m\)个条件,每个条件有2个点\(x,y\)且\(a_x\neq a_y\)。选择最少的\(k\)个点,使其值加\(1\)后,\(m\)个条件仍成立。
solution
考虑如果有一个人选了两个点\(x,y\),且\((a_x+1)\bmod h=a_y\),那么就连一条从\(x\to y\)的有向边。表示如果选了\(x\),就必须选\(y\)。然后将得到的图强连通缩点,容易发现一定是选最小的且出度为0的块。因为如果选了一个出度不为\(0\)的点,之后还要将其他出度为0的点选上,由于是DAG一定有出度为0的点
pii g[N];int tot_e;
vector<int>e[N];
int instk[N],stk[N],top,totscc;
int bel[N],dfn[N],low[N],siz[N],tim;
int n,m,h,isnlef[N];
int a[N];
void tarjan(int u)
{
//printf("%lld\n",u);
low[u]=dfn[u]=++tim;
stk[++top]=u,instk[u]=1;
for(int v:e[u])
{
if(!dfn[v]) tarjan(v),ckmin(low[u],low[v]);
else if(instk[v]) ckmin(low[u],dfn[v]);
}
if(low[u]==dfn[u])
{
++totscc;
while(stk[top+1]!=u)
{
siz[totscc]++;
bel[stk[top]]=totscc;
instk[stk[top--]]=0;
}
}
}
signed main()
{
n=read(),m=read(),h=read();
R(i,1,n) a[i]=read();
int u,v;
R(i,1,m)
{
u=read(),v=read();
if((a[u]+1)%h==a[v]) e[u].pb(v),g[++tot_e]=mkp(u,v);
if((a[v]+1)%h==a[u]) e[v].pb(u),g[++tot_e]=mkp(v,u);
}
R(i,1,n) if(!dfn[i]) tarjan(i);
//test
R(i,1,tot_e)
{
u=bel[g[i].fi],v=bel[g[i].se];
if(u^v) isnlef[u]=1;
}
siz[0]=inf;
int ans=0;
R(i,1,totscc) if(!isnlef[i]&&siz[ans]>siz[i]) ans=i;
writeln(siz[ans]);
R(i,1,n) if(bel[i]==ans) writesp(i);
return 0;
}
2-SAT
SAT指一类对于某一组布尔表达式,求它的一组使得最终结果为1的一组解
布尔表达式都形如:一个条件\(\and\)一个条件\(\and\)一个条件,一个条件是\(a\oplus b\oplus c\ldots \oplus z\)之类的
如果里面的条件只有两个变量就称作2-SAT问题。
如下图就是一个2-SAT
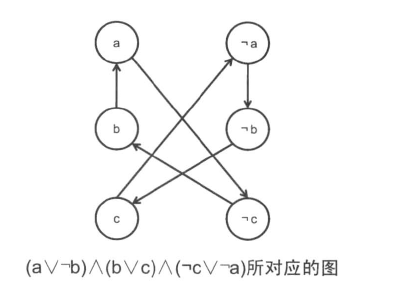
考虑具体怎么求一组合法解:
我们对于每一个变量建两个点,一个表示取真,一个表示取假。
对于一个表达式,我们需要满足它的所有条件
对于如\(a\or \neg b\)的条件,\(a\)取真和\(b\)取假必须满足一个
如果\(a\)取假那么\(b\)也要取假
所以从\(a\)取假向\(b\)取假连一条边
由于\(b\)取真那么\(a\)也要取真,所以从\(b\)取真向\(a\)取真连一条边。
然后对于所有的表达式都进行这样建边,最终就会得到一张图
图中从\(x\)到\(y\)的一条边表示如果要取\(x\)这个状态,那么必须要取\(y\)这个状态。
(2-SAT一条边存在,那么它的逆否命题一定存在)
然后强连通缩点一下
接着对于任何一个\(a\)来说,若\(a\)取真和\(a\)取假在一个强连通分量中,那么是无解的。
\(a\)取真能推到\(a\)取假且\(a\)取假能推到\(a\)取真,那么这显然是错的。
否则的话这个2-SAT是一定有解的
找一个解的话就是\(a\)取真的强连通分量与\(a\)取假的强连通分量比较一下,取拓扑序较大的就行了,这样一定能得到一组合法的解。
void tarjan(int u)
{
low[u]=dfn[u]=++tim;
stk[++top]=u,instk[u]=1;
for(int v:e[u])
{
if(!dfn[v]) tarjan(v),ckmin(low[u],low[v]);
else if(instk[v]) ckmin(low[u],dfn[v]);
}
if(low[u]==dfn[u])
{
++totscc;
/*
do
{
bel[u]=totscc;
instk[u=stk[top--]]=0;
}while(low[u]!=dfn[u]);
*/
while(stk[top+1]!=u)
{
bel[stk[top]]=totscc;
instk[stk[top--]]=0;
}
}
}
signed main()
{
n=read(),m=read();
int u,v,a,b;
R(i,1,m)
{
u=read(),a=read(),v=read(),b=read();
e[u+n*(a&1)].pb(v+n*(b^1));
e[v+n*(b&1)].pb(u+n*(a^1));
}
R(i,1,(n<<1)) if(!dfn[i]) tarjan(i);
R(i,1,n) if(bel[i]==bel[i+n]) return puts("IMPOSSIBLE")&0;
puts("POSSIBLE");
R(i,1,n) printf("%d ",bel[i]<bel[i+n]);
}
例题2
题意:
给定\(n\)个人和\(m\)组限制。限制分为两种:
- 如果\(x\)在\(t\)时间已经死了,则\(y\)在\(t+1\)时间前死了。
- 如果\(x\)在\(t\)时间还活着,则\(y\)在\(t\)时间前死了。
请你对每一个人计算出在\(T+1\)时间时可能与其同时存活的人数。如果这个人在\(T+1\)时刻必然死则答案为0。
\(T\leq 10^6,n\leq 5\times 10^4,m\leq 10^5\)
sol:
对于每一个人在每一个时间点建两个点,一个点代表他在这个时间点还活着,另一个点代表已经死了。然后直接跑2-SAT。
具体建图是对于每一个表示活着的点\((x,t)\),如果这个人在第\(t\)时间还活着,那么他在第\(t-1\)时间一定也活着,所以\((x,t)\to(x,t-1)\)
同理,对于每一个表示死了的点\((x,t)\),如果这个人在第\(t\)时间已经死了,那么他在第\(t+1\)时间一定已经死了,所以\((x,t)\to (x,t+1)\)
然后再按照两个特殊限制相应连边
- 从\((x,t)\)的死亡点,连向\((y,t+1)\)的死亡点
- 从\((x,t)\)的生存点,连向\((y,t)\)的生存点
然后可以发现因为\(T\times N\leq 5\times 10^{10}\)
考虑优化
容易发现对于每一个人来说只有最后的时刻和特殊限制对应的时刻是有用的。于是点数最多只有\(2\cdot (n+m)\)个。
然后考虑因为最后全部都死肯定是一组合法解,所有\(live(x,y)=1\)当且仅当满足以下三个条件:
- \(x\)取真不能推出\(x\)取假。
- \(y\)取真不能推出\(y\)取假。
- \(x\)取真不能推出\(y\)取假。
对于前两个条件考虑直接若某个点出现这个情况就直接把这个点忽略掉就行了。
接下来就是对于每一个没有被忽略的点\(x\),统计有多少个\(y\)满足\(x\)取真不能推出\(y\)取假。
考虑建出的图一定是一个DAG。
因为对于生存状态,因为只有连上死亡状态的边
对于死亡状态来说,对于\(t\)来说,只有\(t\)小的向\(t\)大的连边,所以整个图一定是一个DAG。
直接用bitset维护即可。
(本题中关键点指T+1时刻一定死的点)
具体对于一个DAG,上面的图有一些是关键点,有一些是不关键的点。
对于图上一个点,求它能到达多少个关键点。
令\(dp_{i,j}\)表示第\(i\)开始能否到达\(j\)
转移就是枚举出边,然后从出边或过来
第二维可以压成一个bitset
时间复杂度大概为点数除以一个\(\omega\)。
至于空间问题,每次分10000个关键点做,对于所有点,考虑在10000个中的贡献。
空间复杂度大概就是10000乘点数除以一个\(\omega\)
const int B=10000;
int T,n,m;
int l[555555],d[555555];
map<int,int>live[555555],dead[555555];
int cnt;
int in[555555];
inline int insL(int x,int t)
{
if(!live[x].count(t)) live[x][t]=++cnt;
return live[x][t];
}
inline int insD(int x,int t)
{
if(!dead[x].count(t)) dead[x][t]=++cnt;
return dead[x][t];
}
int qua[5555555],tim;
int can[555555],ans[555555];
vector<int>e[1155555];
inline void add_edge(int u,int v) {e[u].pb(v);in[v]++;}
void toposort()
{
deque<int>q;
int u;
R(i,1,cnt) if(!in[i]) q.pb(i);
while((int)q.size()>0)
{
u=q.front();q.pop_front();
//printf("u:%d\n",u);
qua[++tim]=u;
for(int v:e[u])
{
//printf("v:%d\n",v);
if(!(--in[v])) q.pb(v);
}
}
}
bitset<10010>dp[555555],tmp;
void solve(int L,int R)
{
int u,v;
R(i,L,R) dp[d[i]].set(i-L);
L(i,1,tim)
{
u=qua[i];
for(int v:e[u])
dp[u]|=dp[v];
}
tmp.reset();
R(i,L,R)
{
if(dp[l[i]][i-L]) can[i]=0,tmp[i-L]=1;
else can[i]=1;
}
R(i,1,n) ans[i]+=(R-L+1-(dp[l[i]]|tmp).count());
R(i,1,cnt) dp[i].reset();
}
signed main()
{
T=read(),n=read(),m=read();
R(i,1,n) l[i]=insL(i,T+1),d[i]=insD(i,T+1)/*,printf("%d %d\n",l[i],d[i])*/;
int opt,t,x,y;
R(i,1,m)
{
opt=read(),t=read(),x=read(),y=read();
if(!opt)
{
add_edge(insD(x,t),insD(y,t+1));
add_edge(insL(y,t+1),insL(x,t));
}
else
{
add_edge(insL(x,t),insD(y,t));
add_edge(insL(y,t),insD(x,t));
}
}
int nt;
R(i,1,n)
{
nt=-1;
for(map<int,int>::iterator it=live[i].begin();it!=live[i].end();it++)
{
//printf("l:%d %d\n",it->se,nt);
if(~nt) add_edge(it->se,nt);
nt=it->se;
}
nt=-1;
for(map<int,int>::iterator it=dead[i].begin();it!=dead[i].end();it++)
{
//printf("d:%d %d\n",nt,it->se);
if(~nt) add_edge(nt,it->se);
nt=it->se;
}
}
toposort();
for(int L=1,R=min(n,B);L<=n;L=R+1,R=min(n,L+B-1)) solve(L,R);
R(i,1,n) printf("%d ",!can[i]?0:ans[i]-1);puts("");
}
欧拉回路
首先就是判定一个图中是否有欧拉回路
如果一个图是无向图,它有欧拉回路当且仅当每一个点的度数都为偶数
如果是有向图有欧拉回路,当且仅当所有顶点属于一个强连通分量且每个点出度等于入度。
(前提是整个图是联通的)
如何找欧拉回路呢
圈套圈算法
还是考虑每次随便找一条边出去,然后如果当前无路可走了就把这条边退回来,然后再维护一个栈,表示答案,将这条边加入到栈中,然后不断退,并将边加入到栈中直到又有路可以走了。然后继续走。
具体就是每一次如果当前的点还有边可以走的话就走,如果没有边可以走了就压入一个栈中然后回来,最后栈从顶往底就是一个欧拉回路。
链式前向星213ms
int opt,nok;
int n,m,s;
int vis[400040];
int head[100010],cnt_e;
int stk[200040],top;
struct edge {int nxt,to,id;}e[400040];
inline void add_edge(int u,int v,int d){e[++cnt_e]=(edge){head[u],v,d};head[u]=cnt_e;};
namespace sub1//无向图
{
int deg[100010];
void dfs(int u)
{
for(int i=head[u];i;i=head[u])
{
while(i&&vis[i]) i=e[i].nxt;
head[u]=i;
if(i) vis[i]=vis[i^1]=1,dfs(e[i].to),stk[++top]=e[i].id;
}
}
void mian()
{
cnt_e=1;
n=read(),m=read();
int u,v;
R(i,1,m)
{
u=read(),v=read();
add_edge(u,v,i),add_edge(v,u,-i);
deg[u]++,deg[v]++;s=u;
}
R(i,1,n) if(deg[i]&1){nok=1;break;}
if(nok) {puts("NO");return;}
dfs(s);
if(top^m) puts("NO");
else
{
puts("YES");
L(i,1,top) writesp(stk[i]);puts("");
}
}
}
namespace sub2
{
int in[100010],out[100010];
void dfs(int u)
{
for(int i=head[u];i;i=head[u])
{
while(i&&vis[i]) i=e[i].nxt;
head[u]=i;
if(i) vis[i]=1,dfs(e[i].to),stk[++top]=e[i].id;
}
}
void mian()
{
n=read(),m=read();
int u,v;
R(i,1,m)
{
u=read(),v=read();
add_edge(u,v,i);
in[u]++,out[v]++;s=u;
}
R(i,1,n) if(in[u]^out[u]) {nok=1;break;}
if(nok) {puts("NO");return;}
dfs(s);
if(top^m) {puts("NO");}
else
{
puts("YES");
L(i,1,top) writesp(stk[i]);puts("");
}
}
}
signed main()
{
opt=read();
if(opt==1) sub1::mian();
else sub2::mian();
}
vector322ms
vector<pii>e[200010];
int opt,s;
int n,m;
int vis[200010];
int stk[200020],top;
namespace sub1
{
void dfs(int u)
{
int v,id;
while((int)e[u].size()>0)
{
v=e[u].back().fi,id=e[u].back().se;
e[u].pop_back();
if(!vis[abs(id)])
{
vis[abs(id)]=1;
dfs(v);
stk[++top]=id;
}
}
}
void mian()
{
n=read(),m=read();
int u,v;
R(i,1,m)
{
u=read(),v=read();
e[u].pb(mkp(v,i)),e[v].pb(mkp(u,-i));s=u;
}
R(i,1,n) if(e[i].size()&1){puts("NO");return;}
dfs(s);
if(top^m) puts("NO");
else
{
puts("YES");
L(i,1,top) writesp(stk[i]);puts("");
}
}
}
namespace sub2
{
int in[100010];
void dfs(int u)
{
int v,id;
while((int)e[u].size()>0)
{
v=e[u].back().fi,id=e[u].back().se;
e[u].pop_back();
dfs(v);
stk[++top]=id;
}
}
void mian()
{
n=read(),m=read();
int u,v;
R(i,1,m)
{
u=read(),v=read();
e[u].pb(mkp(v,i));
s=u;
in[v]++;
}
R(i,1,n) if(e[i].size()^in[i]) {puts("NO");return;}
dfs(s);
if(top^m) puts("NO");
else
{
puts("YES");
L(i,1,top) writesp(stk[i]);puts("");
}
}
}
signed main()
{
opt=read();
if(opt==1) sub1::mian();
else sub2::mian();
}
例题3
https://codeforces.com/contest/1361/problem/C
sol:
考虑如何判断答案是否 >=k,将 % 2^k 相同的珍珠分成一组,对于每一组建立一个点。将两个珍珠所在的组连一条边,即需要得到的图中有没有欧拉回路即可。
const int M=(1<<20);
int n,s,nok;
pii a[N];
int stk[N],top;
int cnt_e,head[N];
struct edge {int nxt,to,id;}e[N];
int deg[N],vis[N];
inline void add_edge(int u,int v,int d){e[++cnt_e]=(edge){head[u],v,d};head[u]=cnt_e;}
void dfs(int u)
{
for(int i=head[u];i;i=head[u])
{
while(i&&vis[i]) i=e[i].nxt;
head[u]=i;
if(i) vis[i]=vis[i^1]=1,dfs(e[i].to),stk[++top]=e[i].id;
}
}
signed main()
{
n=read(),cnt_e=1;
int A,B;R(i,1,n)A=read(),B=read(),a[i]=mkp(A,B);
L(j,0,20)
{
R(i,0,M-1) vis[i]=head[i]=deg[i]=0;
cnt_e=1;nok=0;
int mdu=(1<<j)-1;
R(i,1,n)
{
A=a[i].fi&mdu,B=a[i].se&mdu;s=A;
add_edge(A,B,i),add_edge(B,A,-i);\
deg[A]++,deg[B]++;
}
R(i,1,mdu) if(deg[i]&1) {nok=1;break;}
if(nok) continue;
top=0;
dfs(s);
if(top^n) continue;
writeln(j);
L(i,1,top)
{
if(stk[i]>0) writesp(2*abs(stk[i])-1),writesp(2*abs(stk[i]));
else writesp(2*abs(stk[i])),writesp(2*abs(stk[i])-1);
}
return 0;
}
}
割顶和桥
对于无向图G,如果删除某个节点u之后,连通分量数目增加,则称u为图的割顶
如果删除某条边后,连通分量数目增加,则称该边为图的桥。
所有割顶和桥都可以使用tarjan算法求出
tarjan算法
对图进行dfs并找出一棵dfs树。
维护两个数组\(dfn\)和\(low\),\(dfn\)表示\(dfs\)序,\(low\)表示它自身以及它的子树的返祖边的\(dfn\)的最小值。
关于找出所有桥
如果一条树边\(u\to v\)满足\(low[v]>dfn[u]\)那么\(u\to v\)一定是桥
而非树边一定不是桥,所以就找出了所有的桥
关于找割顶
对于非根节点\(u\),如果\(u\)有一个儿子\(v\)满足\(low[v]\ge dfn[u]\),那么\(u\)一定是一个割顶。
但是对于根节点不满足这种情况,所以要特判掉。
双连通图
双连通图分为点双连通图和边双连通图。
点双连通图的定义为在图中对于任意两个点\(x,y\)都存在两条点不相交的路径从\(x\)到\(y\)(路径不包含\(x\)和\(y\))即不存在割顶。边双连通图的定义为在图中对于任意两个点\(x,y\)都存在两条边不相交的路径从\(x\)到\(y\),即不存在桥。
无向图的极大点/边双连通子图,称作该图的点/边双连通分量。(就类似强连通分量)
如何求点双连通分量
由于点双连通分量一定是由割顶组成的,所以说每找到一个割顶就相当于找到一个点双连通分量。考虑当前走到了\(u\to v\)且\(low[v]\ge dfn[u]\),那么\(v\)下面包含\(u\)的某一块就一定是一个点双连通分量。
具体是用在访问到\(v\)之前,用一个栈把访问到的边都记录下来包括\(u\to v\),然后从\(v\)访问回来后,肯定还会留下一些边,所以就不断弹栈直到当前的边是\(u\to v\)为止。然后弹出来的那些边都是点双连通分量的一个点集。不断做就找出了所有点双连通分量。
就是说我们在从\(u\)转移到\(v\)之前,把\(u\to v\)这条边加入某一个栈中,然后考虑这个\(v\)下去又搜了一些又弹了一些最后又剩下一些边,把这些边弹出来,然后考虑这些边的点集就是点双连通分量的点集。
如何求边双连通分量
对于任意一个图来说,它的边双连通分量是由桥分割开的。所以求边双连通分量就很简单了,先求出所有的桥,然后将所有的桥都断掉,剩下的每一个连通块都是原图的一个边双连通分量。
例题四

Sample Input
5 11
94 37 60 30 24
3 5 4
3 4 1
1 1 4
3 1 1
3 5 4
1 2 5
2 1 17
1 4 5
3 2 3
1 2 3
3 3 5
Sample Output
-1
-1
94
-1
-1
121
Data Constraint
对于15%的数据,\(N,M\leq 10\)。
对于25%的数据,\(N,M\leq 100\)。
对于45%的数据,\(N,M\leq 1000\)。
对于70%的数据,\(N,M\leq 10000\)
对于100%的数据,\(N,M\leq 150000,W_i\leq 10000\)。
本题来自网上找来的题解和代码
如果形成了一个环,那么可以缩成一个点,这个点的权值就是这个连通分量的答案。然后相当于找树上路径最大值,考虑lct维护。
当我们连成一个环时,我们保留一个代表点,维护一个并查集,使原来路径上所有点指向这个点,把他们的权值都给这个点,然后把整棵splay的边弄断。然后每次找一个点父亲时,要在并查集上getfa一下,顺便把这个点的父亲指向getfa得到的点。
以及实际题好像是操作2是增加b...
#include <iostream>
#include <cmath>
#include <cstdio>
const int maxn=150007;
using namespace std;
int n,m,x,y,op;
int p[maxn],acc[maxn];
struct node{
int l,r,fa;
int data,sum;
int rev;
}t[maxn];
int getfa(int x)
{
if (!p[x]) return x;
return (p[x]=getfa(p[x]));
}
void union1(int x,int y)
{
int u=getfa(x),v=getfa(y);
if (u==v) return;
p[v]=u;
}
void updata(int x)
{
t[x].sum=t[x].data+t[t[x].l].sum+t[t[x].r].sum;
}
bool isroot(int x)
{
t[x].fa=getfa(t[x].fa);
return ((t[t[x].fa].l!=x) && (t[t[x].fa].r!=x));
}
void rttr(int x)
{
int y=t[x].l;
t[x].l=t[y].r;
if (t[y].r) t[t[y].r].fa=x;
t[x].fa=getfa(t[x].fa);
if (x==t[t[x].fa].l) t[t[x].fa].l=y;
else if (x==t[t[x].fa].r) t[t[x].fa].r=y;
t[y].fa=getfa(t[y].fa);
t[y].fa=t[x].fa;
t[x].fa=y;
t[y].r=x;
updata(x); updata(y);
}
void rttl(int x)
{
int y=t[x].r;
t[x].r=t[y].l;
if (t[y].l) t[t[y].l].fa=x;
t[x].fa=getfa(t[x].fa);
if (x==t[t[x].fa].l) t[t[x].fa].l=y;
else if (x==t[t[x].fa].r) t[t[x].fa].r=y;
t[y].fa=getfa(t[y].fa);
t[y].fa=t[x].fa;
t[x].fa=y;
t[y].l=x;
updata(x); updata(y);
}
void remove(int x)
{
if (!isroot(x)) remove(t[x].fa=getfa(t[x].fa));
if (t[x].rev)
{
t[x].rev^=1;
swap(t[x].l,t[x].r);
if (t[x].l) t[t[x].l].rev^=1;
if (t[x].r) t[t[x].r].rev^=1;
}
}
void splay(int x)
{
remove(x);
while (!isroot(x))
{
int p=t[x].fa=getfa(t[x].fa),g=t[p].fa=getfa(t[p].fa);
if (isroot(p))
{
if (x==t[p].l) rttr(p);
else rttl(p);
}
else
{
if (x==t[p].l)
{
if (p==t[g].l) rttr(p),rttr(g);
else rttr(p),rttl(g);
}
else
{
if (p==t[g].l) rttl(p),rttr(g);
else rttl(p),rttl(g);
}
}
}
}
void access(int x)
{
int y=0;
while (x)
{
splay(x);
t[x].r=y;
updata(x);
y=x,x=t[x].fa=getfa(t[x].fa);
}
}
void makeroot(int x)
{
access(x);
splay(x);
t[x].rev^=1;
}
void link(int x,int y)
{
makeroot(x);
access(y);
splay(y);
t[x].fa=y;
}
void solve(int x,int root)
{
if (x!=root) t[root].data+=t[x].data;
union1(root,x);
if (t[x].l) solve(t[x].l,root);
if (t[x].r) solve(t[x].r,root);
t[x].l=0;
t[x].r=0;
}
int find(int x)
{
if (!acc[x]) return x;
return (acc[x]=find(acc[x]));
}
void union2(int x,int y)
{
int u=find(x),v=find(y);
if (u==v) return;
acc[u]=v;
}
int main()
{
freopen("graph.in","r",stdin);
freopen("graph.out","w",stdout);
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++)
{
scanf("%d",&t[i].data);
t[i].sum=t[i].data;
}
for (int i=1;i<=m;i++)
{
scanf("%d%d%d",&op,&x,&y);
if (op==1)
{
x=getfa(x); y=getfa(y);
if (find(x)!=find(y))
{
link(x,y);
union2(x,y);
}
else
{
makeroot(x);
access(y);
splay(y);
solve(y,y);
}
}
if (op==2)
{
x=getfa(x);
t[x].data+=y;
t[x].sum+=y;
}
if (op==3)
{
x=getfa(x); y=getfa(y);
if (find(x)!=find(y)) printf("-1\n");
else
{
makeroot(x);
access(y);
splay(y);
printf("%d\n",t[y].sum);
}
}
}
}
考虑如果将一个边双连通分量缩成一个点的话,那么缩点后一定是一个森林。且从 a 到 b 能走到的点就是树上 a 所在的边双到 b 所在的边双的路径上所有边双内的点。于是剩下的问题就是怎么维护边双连通分量缩点的问题,考虑加入一条边 x,y,如果 x 和 y 本来就连通,那么显然我们要把 x 到 y 路径上所有的点缩成一个点。如果不连通的话就直接加入 x 到 y 的这条边,直接用 LCT 维护即可。
圆方树
圆方树分为狭义圆方树和广义圆方树。
狭义圆方树
主要用来处理仙人掌上的问题。
对于一个环,把环上的所有边都删掉,然后建一个方点与环上的所有圆点连一条边。
圆方图的主要用处是用来把仙人掌变成一棵树,然后就可以用树上的一些操作来解决仙人掌上的问题
比如某一些在仙人掌上dp,就可以通过把它转成圆方树,然后把它转成树形dp。
广义圆方树
广义圆方树可以对任意图建圆方树。
具体做法是先去掉原图中所有的边,对于每一个点双连通分量新建一个方点,并将这个点双内的所有点与该点相连。
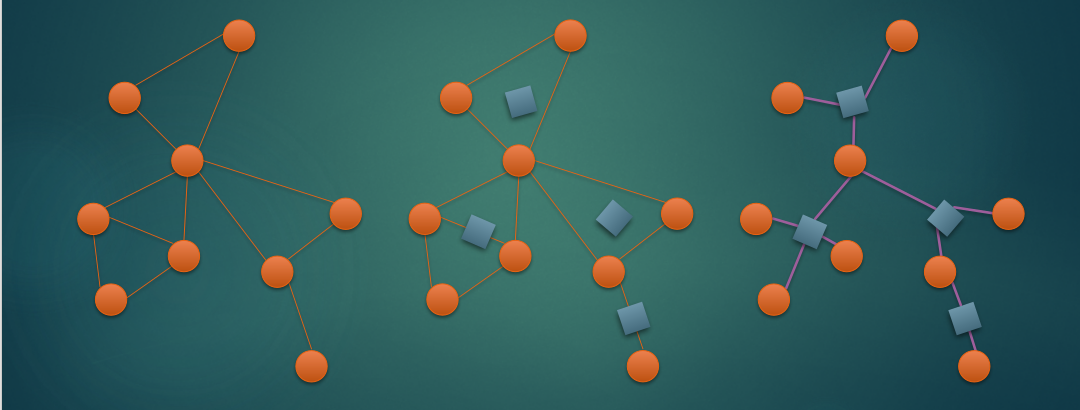
广义圆方树的一些性质
- 相邻的两个点类型一定不同,即圆点只能和方点相邻,方点只能和圆点相邻。
- 一个点到另一个点的所有路径的交集为在圆方树上这两个点的路径上所有的圆点。
- 一个点到另一个点的所有简单路径的并集为在圆方树上这两个点的路径上所有的方点表示的点双内的点的并集。
例题5
圆方树模板题,考虑如果对于每一个方点维护与它相邻的圆点的权值的最小值,那么答案就是在圆方树上从\(a\)到\(b\)的路径上放点的权值的最小值。
考虑如果这样维护的话,修改可能会修改\(O(n)\)个方点(菊花图)。于是考虑对于每一个方点维护除父亲以外与它相邻的圆点的权值最小值,这样每次只可能修改一个方点的值,注意当两个询问点的lca为方点时,还需要把\(lca\)的父亲算上去。
树链剖分维护即可,当然还可以写LCT。
int totds;
int n,m,q,w[200020];
struct dheap
{
priority_queue<int,vector<int>,greater<int> >q,qd;
inline void ins(int x) {q.push(x);}
inline void era(int x) {qd.push(x);}
inline int top()
{
if(q.size()==qd.size()) return inf;
while(qd.size()&&q.top()==qd.top()) q.pop(),qd.pop();
return q.top();
}
}s[100010];
namespace yfs
{
vector<int>e[200020];
int fa[200020],htop[200020],hson[200020],id[200020];
int siz[200020],dep[200020],st[200020],tim;
int mn[800080];
inline void add_edge(int u,int v) {e[u].pb(v);e[v].pb(u);}
void dfs1(int u)
{
siz[u]=1;
for(int v:e[u]) if(v^fa[u])
{
fa[v]=u,dep[v]=dep[u]+1;
dfs1(v);
siz[u]+=siz[v];
hson[u]=(siz[v]>siz[hson[u]])?v:hson[u];
}
if(fa[u]>n) {s[fa[u]-n].ins(w[u]);}
}
void dfs2(int u,int topf)
{
htop[u]=topf;st[u]=++tim;id[tim]=u;
if(hson[u]) dfs2(hson[u],topf);
for(int v:e[u]) if(v^fa[u]&&v^hson[u]) dfs2(v,v);
}
inline void push_up(int x) {mn[x]=min(mn[x<<1],mn[x<<1|1]);}
void build(int l,int r,int x)
{
if(l==r) {mn[x]=w[id[l]];return;}
int mid=(l+r)>>1;
build(l,mid,x<<1),build(mid+1,r,x<<1|1);
push_up(x);
}
void modify(int p,int l,int r,int x,int k)
{
if(l==r) {mn[x]=k;return;}
int mid=(l+r)>>1;
if(p<=mid) modify(p,l,mid,x<<1,k);
else modify(p,mid+1,r,x<<1|1,k);
push_up(x);
}
int query(int L,int R,int l,int r,int x)
{
if(L<=l&&r<=R) return mn[x];
int mid=(l+r)>>1,ret=inf;
if(L<=mid) ckmin(ret,query(L,R,l,mid,x<<1));
if(mid<R) ckmin(ret,query(L,R,mid+1,r,x<<1|1));
return ret;
}
int query_path(int u,int v)
{
int ret=inf;
while(htop[u]^htop[v])
{
if(dep[htop[u]]<dep[htop[v]]) swap(u,v);
ckmin(ret,query(st[htop[u]],st[u],1,totds,1));
u=fa[htop[u]];
}
if(dep[u]>dep[v]) swap(u,v);
ckmin(ret,query(st[u],st[v],1,totds,1));
if(u>n) ckmin(ret,w[fa[u]]);
return ret;
}
void print()
{
puts("");
puts("---------------------hooooooooooooooooo--------------------");
printf("mn:");R(i,1,20) printf("%lld ",mn[i]);puts("");
puts("---------------------qwwwwwwwwwwwwwwwww--------------------");
puts("");
}
void mian()
{
yfs::dep[1]=1;
dfs1(1);
dfs2(1,1);
R(i,n+1,totds) w[i]=s[i-n].top();
build(1,totds,1);
// print();
}
}
namespace yg
{
int stk[100010],top;
int low[100010],dfn[100010],tim,fa[100010];
vector<int>e[100010];
inline void add_edge(int u,int v) {e[u].pb(v),e[v].pb(u);}
void tarjan(int u)
{
low[u]=dfn[u]=++tim;
stk[++top]=u;
for(int v:e[u]) if(v^fa[u])
{
fa[v]=u;
if(!dfn[v])
{
tarjan(v);
ckmin(low[u],low[v]);
if(low[v]>=dfn[u])
{
w[++totds]=inf;
yfs::add_edge(u,totds);
do yfs::add_edge(stk[top],totds);while(stk[top--]^v);
}
}
else ckmin(low[u],dfn[v]);
}
}
}
signed main()
{
totds=n=read(),m=read(),q=read();
R(i,1,n) w[i]=read();
int u,v,l;R(i,1,m) u=read(),v=read(),yg::add_edge(u,v);
yg::tarjan(1);
yfs::mian();
char opt[5];
while(q--)
{
scanf("%s",opt+1);
u=read(),v=read();
if(opt[1]=='C')
{
l=yfs::fa[u];
if(l)
{
s[l-n].era(w[u]),s[l-n].ins(v);
yfs::modify(yfs::st[l],1,totds,1,w[l]=s[l-n].top());
}
yfs::modify(yfs::st[u],1,totds,1,w[u]=v);
/*
yfs::modify(yfs::st[u],1,totds,1,v);
if(u==1){w[u]=v;continue;}
l=yfs::fa[u];
s[l-n].era(w[u]),s[l-n].ins(v);
int minn=s[l-n].top();
if(minn==w[l]){w[u]=v;continue;}
yfs::modify(yfs::st[l],1,totds,1,minn);
w[l]=minn,w[u]=v;
*/
}
if(opt[1]=='A') writeln(yfs::query_path(u,v));
}
}
网络流
给你一个图,有个源点有个汇点,每条边有一定的流量限制,求从源点到汇点最多能留多少流量。
一个比较直观的做法是不断dfs找一个可行的增广路知道没有增广路为止。但显然不太对。所以要增加一个反向流量,即反悔操作。
ford-fulkerson 算法
暴力 dfs 模拟增广过程(即上面所说的做法
时间复杂度 \(O(Fm)\)。其中\(F\)为最大流量。
Dinic算法
每次只考虑增广到 s 距离差为 1 的边。
时间复杂度 \(O(n^2m)\)。
具体做法是对于一个图,算出来从\(S\)到其他所有点的距离,假如有一条边\(x\to y\),如果\(dist_x+1=dist_y\),那么就把这条边加入可以增广的边的集合,否则就不管这条边。然后再从\(S\)进行一次dfs,然后对于可行的边增广一下就行了。容易发现一次增广的复杂度最快是\(O(nm)\)的,每次增广之后\(S\to T\)的最短距离一定会变所以距离最多只会变\(n\)次,时间复杂度为\(O(n^2m)\)的。
Dinic的一些优化
都是在一些增广途中的一些优化
当前弧优化
就大概目前从\(p\to x\),而\(x\)已经访问了一些边如\(e_1,e_2\)且这些边已经没有多余的流量了,假设现在访问\(e_3\),所以假如之后有一个点\(k\)再去访问\(x\)之后,就没有必要再去访问\(e_1,e_2\)了。
就对每一个\(x\)记一个当前出边,当他退出之后就不用访问出边前的出边了。
炸点优化
比如说当前是\(x\)去访问了\(y\),如果\(y\)不能再流任何流量了,就把\(y\)炸掉,之后某个点访问\(y\)之后就不让它进行下去了。(比如设成-inf)。
(似乎不加当前弧优化的dinic复杂度是错的。
int n,m,S,T;
ll dis[555555],ans;
int tot_e=1,head[555555],now[555555];
struct edge
{
int nxt,to;ll val;
edge() {}
edge(int n,int t,int v) {nxt=n,to=t,val=v;}
}e[555555];
inline void add_edge(int u,int v,ll d)
{
e[++tot_e]=edge(head[u],v,d);head[u]=tot_e;
}
deque<int>q;
int bfs(int s)
{
fill(dis,dis+n+2,inf);
q.clear();
q.pb(s);
dis[s]=0;
now[s]=head[s];
int u,v;
while((int)q.size()>0)
{
u=q.front();q.pop_front();
for(int i=head[u];i;i=e[i].nxt)
{
v=e[i].to;
if(e[i].val>0&&dis[v]==inf)
{
q.pb(v);
now[v]=head[v];
dis[v]=dis[u]+1;
if(v==T) return 1;
}
}
}
return 0;
}
int dfs(int u,ll sum)
{
if(T==u) return sum;
ll k;
int v;
ll res=0;//k为当前最小的剩余容量
for(int i=now[u];i&∑i=e[i].nxt)
{
v=e[i].to;
if(e[i].val>0&&(dis[v]==dis[u]+1))
{
k=dfs(v,min(sum,e[i].val));
if(!k) dis[v]=inf;
e[i].val-=k,e[i^1].val+=k;
res+=k,sum-=k;
}
}
return res;
}
signed main()
{
n=read(),m=read(),S=read(),T=read();
int u,v;ll d;R(i,1,m)u=read(),v=read(),d=read(),add_edge(u,v,d),add_edge(v,u,0);
while(bfs(S)) ans+=dfs(S,inf);
writeln(ans);
}
之后如果无聊的话可能会补个HLPP
max-flow min-cut 定理
在任何网络中,max-flow=min-cut
考最大流一般都会考最小割模型
例题6
https://codeforces.com/contest/1082/problem/G
题意:
定义图权\(=\)图中边权总和\(-\)图中点权总和(空图的图权\(=0\)),求\(n\)个点\(m\)条边的无向图最大子权图。
sol:

以上搬运自神sooke的题解
经典的最小割模型,对于每一条边额外建立一个点。先假设所有边都选了,然后求删去一些选的边,并加入一些点,使得最终合法的最小的代价。考虑从源点向每个表示表示边的点连一条容量为该边权的边,每个表示点的点向汇点连一条容量为点权的边。然后每个表示边的点向两端的点连一条容量为inf的边,一种合法的方案即为一种没有割到inf边的割。直接求最小割即可。
关于连边的图大概就长这个样子....

考虑这个建图是什么意思,就是考虑显然会割一些左边的边,再去割一些右边的边,就先假设所有边都选,然后考虑如果割了左边的边,就表示左边的边被删除了,然后如果割了右边的边,就表示右边的边被选进去了,如果我们想选一个边,就要去割他两端的点所表示的边(因为不能割inf)。
int n,m,s,t;
int dis[55555],ans;
int cnt_e=1,head[55555],now[55555];
struct edge{int nxt,to,val;}e[1000010];
inline void add_edge(int u,int v,int d) {e[++cnt_e]=(edge){head[u],v,d};head[u]=cnt_e;}
inline void link(int u,int v,int d){add_edge(u,v,d),add_edge(v,u,0);}
deque<int>q;
int bfs()
{
fill(dis,dis+(n+m)*2+10,inf);
q.clear();
q.pb(s);
dis[s]=0;
now[s]=head[s];
int u,v;
while((int)q.size()>0)
{
u=q.front();q.pop_front();
for(int i=head[u];i;i=e[i].nxt)
{
v=e[i].to;
if(e[i].val>0&&dis[v]==inf)
{
q.pb(v);
now[v]=head[v];
dis[v]=dis[u]+1;
if(v==t) return 1;
}
}
}
return 0;
}
int dfs(int u,int sum)
{
if(t==u) return sum;
int k,v,res=0;
for(int i=now[u];i&∑i=e[i].nxt)
{
v=e[i].to;
if(e[i].val>0&&(dis[v]==dis[u]+1))
{
k=dfs(v,min(sum,e[i].val));
if(!k) dis[v]=-inf;
e[i].val-=k,e[i^1].val+=k;
res+=k,sum-=k;
}
}
return res;
}
signed main()
{
n=read(),m=read(),s=0,t=n+m+1;
int u,v,d;
R(i,1,n) d=read(),link(i,t,d);
R(i,1,m) u=read(),v=read(),d=read(),link(n+i,u,inf),link(i+n,v,inf),link(s,i+n,d),ans+=d;
while(bfs()) ans-=dfs(s,inf);
writeln(ans) ;
}
最小费用流
问题就是有一个网络,每条边不止有一个流量了,还有一个费用,你每流一个流量还有一个费用。我们现在要求从\(S\)到\(T\),流\(F\)的流量最小需要多少费用。
考虑一种做法就是,我们每一次直接找到\(S\to T\)的最短路,边权是流过这条边所需要的费用,然后在最短路上流相应的流量,直到流完\(F\)就可以了。
然后如果直接SPFA最坏复杂度\(O(Fnm)\)
采用势能函数即可dijkstra,复杂度可以降到\(O(Fm\log n)\)
具体做法:
考虑网络流一般为什么不能dijkstra
从\(x\to y\)连一条边权为\(c\)的边,就会有从\(y\to x\)连一条\(-c\)的边,即负权边是一定存在的,所以我们就不能跑dijkstra。
考虑三角不等式
势函数\(dist\)指:
对于新图上求出\(S\)到每个点的最短路,那么考虑一个点\(S\)到某一个点\(x\)新的距离
那么\(dist_x+c\ge dist_y\)
即\(dist_x+c-dist_y\ge 0\)
将边权\(c\)改为\(dist_x+c-dist_y\)
对于任意一条\(S\to T\)的路径来说,它的实际的费用其实是它在新图上的费用\(cost+dist_t\)
就比如原来的路径是\(S\to x_1\to x_2\to x_3\to T\),边权为\(c_1,c_2,c_3,c_4\)
那么修改之后路径边权和为
全部消掉后只剩下\(c_1+c_2+c_3+c_4+dist_S-dist_T\),且由于\(dist_S=0\),所以不用管。
通过上述操作就将所有边都弄成正权了。
zkw费用流
https://artofproblemsolving.com/community/c1368h1020435
不一条一条增广,
而跑出一个最短路图(即保留所有的边\(x\to y\)满足\(dist_x+cost(x,y)=dist_y\))
在保留的边上跑dinic即可。
最小费用最大流(MCMF)
把流量F设为当前网络的最大流,然后跑一遍费用流,做法就是不断增广最短路直到不能增广为止。
洛谷和loj上的板子:
#include<bits/stdc++.h>
#define ld long double
#define tset puts("qwq");
#define test puts("QAQ");
#define pb(a) push_back(a)
#define pii pair<int,int>
#define mkp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define int long long
#define R(i,a,b) for(int i=(a),i##E=(b);i<=i##E;i++)
#define L(i,a,b) for(int i=(b),i##E=(a);i>=i##E;i--)
#define clr(f,n) memset(f,0,sizeof(int)*(n))
#define cpy(f,g,n) memcpy(f,g,sizeof(int)*(n))
template <typename T> bool ckmax(T &x, T y) { return x<y?x=y,true:false;}
template <typename T> bool ckmin(T &x, T y) { return x>y?x=y,true:false;}
using namespace std;
//const ll inf=0x7f7f7f7f7f7f7f3f;
const ll inf=(1ll<<60);
//const int inf=0x7f7f7f7f;
//const int mod=1e9+7;
const double Pi=acos(-1);
const int mod=1e9+7;
const double eps=1e-6;
inline int fpow(int a,int b=mod-2,int p=mod){a%=p;int res=1;while(b){if(b&1)res=res*a%p;a=a*a%p;b>>=1;}return res;}
inline ll read()
{
char c=getchar();ll x=0;bool f=0;
for(;!isdigit(c);c=getchar())f^=!(c^45);
for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
if(f)x=-x;
return x;
}
inline void write(ll x){if (x<0){putchar('-');write(-x);return;}if (x>=10) write(x/10);putchar(x%10+'0');}
inline void writesp(ll x){write(x),putchar(' ');}
inline void writeln(ll x){write(x);putchar('\n');}
int head[50050],dis[50050],vis[50050],h[50500];
int n,m,s,t,cnt_e=1,MXF,MNC;
struct edge {int nxt,to,val,cos;}e[500010];
inline void add_edge(int u,int v,int d,int c)
{
e[++cnt_e]=(edge){head[u],v,d,c};head[u]=cnt_e;
}
inline void link(int u,int v,int d,int c)
{
add_edge(u,v,d,c),add_edge(v,u,0,-c);
}
void spfa()
{
deque<int>q;
R(i,1,n+1) h[i]=inf;
h[s]=0;vis[s]=1;
q.pb(s);int u,v;
while((int)q.size()>0)
{
u=q.front();q.pop_front();
vis[u]=0;
for(int i=head[u];i;i=e[i].nxt)
{
v=e[i].to;
if(e[i].val&&h[v]>h[u]+e[i].cos)
{
h[v]=h[u]+e[i].cos;
if(!vis[v]) vis[v]=1,q.pb(v);
}
}
}
}
struct node
{
int val,pos;
inline int operator <(const node &A)const {return val>A.val;}
};
pii p[50010];
int dij()
{
priority_queue<node>q;
R(i,1,n+1) dis[i]=inf,vis[i]=0;
dis[s]=0;
q.push((node){0,s});
int u,v,tc;
while((int)q.size()>0)
{
u=q.top().pos;q.pop();
if(vis[u]) continue;vis[u]=1;
for(int i=head[u];i;i=e[i].nxt)
{
v=e[i].to,tc=e[i].cos+h[u]-h[v];
if(e[i].val&&dis[v]>dis[u]+tc)
{
dis[v]=dis[u]+tc;
p[v]=mkp(u,i);
if(!vis[v]) q.push((node){dis[v],v});
}
}
}
return dis[t]!=inf;
}
signed main()
{
n=read(),m=read(),s=read(),t=read();
int u,v,d,c,minF;
R(i,1,m) u=read(),v=read(),d=read(),c=read(),link(u,v,d,c);
spfa();
while(dij())
{
//printf("%lld\n",dis[t]);
minF=inf;
R(i,1,n) h[i]+=dis[i];
for(int i=t;i^s;i=p[i].fi) ckmin(minF,e[p[i].se].val);
for(int i=t;i^s;i=p[i].fi) e[p[i].se].val-=minF,e[p[i].se^1].val+=minF;
MXF+=minF,MNC+=minF*h[t];
}
writesp(MXF),writeln(MNC);
}
UOJ上的板子:
讲解:ouuan
dijkstra的板子(菜鸡并不会写:
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef pair<ll, int> pli;
const ll INF = 1e18;
const ll LARGE = 1e12;
int n, m;
vector<bool> vis;
vector<int> head, nxt, from, to, pre;
vector<ll> raw_cap, cap, cost, p, dis;
priority_queue<pli, vector<pli>, greater<pli> > q;
void add(int u, int v, ll f, ll w)
{
nxt.push_back(head[u]);
head[u] = to.size();
from.push_back(u);
to.push_back(v);
raw_cap.push_back(f);
cap.push_back(0);
cost.push_back(w);
}
void add_edge(int u, int v, ll f, ll w)
{
add(u, v, f, w);
add(v, u, 0, -w);
}
ll c(int id)
{
return p[from[id]] + cost[id] - p[to[id]];
}
void dijkstra(int s)
{
vis.assign(n + 2, false);
dis.assign(n + 2, INF);
pre.assign(n + 2, -1);
dis[s] = 0;
q.push(pli(0, s));
while (!q.empty())
{
int u = q.top().second;
ll w = q.top().first;
q.pop();
if (vis[u]) continue;
vis[u] = true;
for (int i = head[u]; ~i; i = nxt[i])
{
int v = to[i];
if (cap[i] && dis[v] > w + c(i))
{
dis[v] = w + c(i);
pre[v] = i;
q.push(pli(dis[v], v));
}
}
}
}
void add_one_cap(int id)
{
int u = from[id];
int v = to[id];
if (cap[id])
{
++cap[id];
return;
}
dijkstra(v);
if (dis[u] < INF && dis[u] + c(id) < 0)
{
++cap[id ^ 1];
while (u != v)
{
int x = pre[u];
--cap[x];
++cap[x ^ 1];
u = from[x];
}
}
else ++cap[id];
ll max_dis = 0;
ll cur_len = c(id);
for (int i = 1; i <= n; ++i) if (dis[i] < INF) max_dis = max(max_dis, dis[i]);
for (int i = 1; i <= n; ++i) p[i] += dis[i] < INF ? dis[i] : max_dis + max(0ll, -cur_len);
dijkstra(n + 1);
for (int i = 1; i <= n; ++i) p[i] += dis[i];
}
int main()
{
int s, t;
cin >> n >> m >> s >> t;
head.resize(n + 2, -1);
p.resize(n + 2, 0);
for (int i = 1; i <= m; ++i)
{
ll u, v, f, w;
cin >> u >> v >> f >> w;
add_edge(u, v, f, w);
}
add_edge(t, s, LARGE, -LARGE);
for (int i = 1; i <= n; ++i)
{
add_edge(n + 1, i, 0, 0);
cap[to.size() - 2] = 1;
}
for (int i = 40; i >= 0; --i)
{
for (int j = 0; j <= m * 2 + 1; ++j) cap[j] <<= 1;
for (int j = 0; j <= m * 2; j += 2)
{
if ((raw_cap[j] >> i) & 1)
{
add_one_cap(j);
}
}
}
ll min_cost = 0;
for (int i = 0; i < m; ++i) min_cost += cap[i << 1 | 1] * cost[i << 1];
cout << cap[m << 1 | 1] << ' ' << min_cost;
return 0;
}
SPFA,跑得飞快:
int n,m,s,t;
struct edge {int nxt,to,cap,cos;}e[2000010];
int raw_cap[10100];
int head[10100],cnt_e=1;
int u[10100],v[10100],c[10010],id[10100];
inline void add_edge(int u,int v,int c) {e[++cnt_e]=(edge){head[u],v,0,c};head[u]=cnt_e;}
inline void link(int u,int v,int c) {add_edge(u,v,c),add_edge(v,u,-c);}
int dis[10010],pre[10100],vis[10100];
deque<int>q;
const ll INF=1e12;
inline int spfa(int s,int t)
{
//printf("s:%lld t:%lld\n",s,t);
R(i,0,n+5) dis[i]=inf;
dis[s]=0;
q.pb(s);
vis[s]=1;
int u,v;
while((int)q.size()>0)
{
u=q.front();q.pop_front();
vis[u]=0;
for(int i=head[u];i;i=e[i].nxt)
{
v=e[i].to;
if(e[i].cap&&dis[v]>dis[u]+e[i].cos)
{
dis[v]=dis[u]+e[i].cos;
pre[v]=i;
if(!vis[v]) vis[v]=1,q.pb(v);
}
}
}
return dis[t]<inf;
}
signed main()
{
n=read(),m=read(),s=read(),t=read();
R(i,1,m) u[i]=read(),v[i]=read(),raw_cap[i]=read(),c[i]=read(),id[i]=cnt_e,link(u[i],v[i],c[i]);
++m;
u[m]=t,v[m]=s,raw_cap[m]=INF,c[m]=-inf,id[m]=cnt_e;link(u[m],v[m],c[m]);
L(i,0,40)
{
R(j,2,cnt_e) e[j].cap<<=1;
R(j,1,m)
{
if((raw_cap[j]>>i)&1)
{
if(spfa(v[j],u[j])&&dis[u[j]]+c[j]<0)
{
for(int i=u[j];i!=v[j];i=e[pre[i]^1].to)
{
e[pre[i]].cap--;
e[pre[i]^1].cap++;
}
e[id[j]+2].cap++;
}
else e[id[j]+1].cap++;
}
}
}
ll ans=0;
R(i,1,m-1) ans+=1ll*c[i]*e[id[i]+2].cap;
writesp(e[id[m]+2].cap),writeln(ans);
}
例题7
https://community.topcoder.com/stat?c=problem_statement&pm=12432
题意:
有一个矩阵,里面有一些格子是堵住的,有一些格子是没有堵住的。在一些没有堵住的格子上可能会有一个生物。在没有被堵住的格子上四个方向铺设铁路,必须满足铁路形成若干个环,接着这些生物都比较喜欢弯曲,如果当前生物在某个格子上,如果连接这个格子的一条铁路是直的,这个生物就会不高兴,否则就会很高兴,要求一种方案使不高兴的生物最少,输出最少不高兴的生物的个数。
solution
考虑格子是一个二分图,把铁路看成两两匹配,然后对于每一个格子,每四个方向建一个点,再对上下和左右方向各建一个点,然后向这两个点连一条容量为1,费用为0的流,再连一条容量为1,费用为1的流。
如果一个点向右边连了一条边,那么它右边的那个点也要向左连一条边。
因为相邻的条件是一个二分图,先把它黑白图染色。
对于某一个方向下,找到它右边下面对应的点的方向上,然后下到上连一条边。
相当于一个流量这确定了两个方向。然后考虑具体图怎么建。
对于每个点,先把它拆成两个大方向:上下和左右。再把两个大方向拆成两个小方向,然后黑点的小方向与白点的小方向对应连边。
接着考虑大方向的费用如何处理
经过一次大方向的费用是0,然后经过两次大方向的费用为1。
所以就连一条费用为0流量为1的边,再连一条费用为1流量为1的边即可。
以及注意,如果不能满流,即无解。

最后的图大概就这个样子...
先连一条费用为0的边,再连一条费用为1的边,大概就还是费用流比较常见的连边方式...
比如一条边经过\(a\)次费用是\(a^2\),那么就可以连一条费用为1的边,费用为3的边,费用为5的边...如果费用是个凸函数,就都可以按照这种方式连边。
const int dx[]={0,-1,0,1};
const int dy[]={1,0,-1,0};
const int N=30010;
const int INF=0x3f3f3f3f;
int head[N],dis[N],vis[N],h[N];
int n,m,s,t,cnt_e=1,MXF,MNC;
int id[3310][33][5];
std::vector<string> field;
struct edge {int nxt,to,cap,cos;}e[150010];
inline void add_edge(int u,int v,int f,int c)
{
e[++cnt_e]=(edge){head[u],v,f,c};head[u]=cnt_e;
}
inline void link(int u,int v,int f,int c)
{
//printf("u:%d v:%d f:%d c:%d\n",u,v,f,c);
add_edge(u,v,f,c),add_edge(v,u,0,-c);
}
inline void Add(int u,int v,int opt)
{
if((u+v)%2==0)
{
link(s,id[u][v][0],2,0);
if(!opt)
{
link(id[u][v][0],id[u][v][1],2,0);
link(id[u][v][0],id[u][v][2],2,0);
}
else
{
link(id[u][v][0],id[u][v][1],1,0);
link(id[u][v][0],id[u][v][1],1,1);
link(id[u][v][0],id[u][v][2],1,0);
link(id[u][v][0],id[u][v][2],1,1);
}
}
else
{
link(id[u][v][0],t,2,0);
if(!opt)
{
link(id[u][v][1],id[u][v][0],2,0);
link(id[u][v][2],id[u][v][0],2,0);
}
else
{
link(id[u][v][1],id[u][v][0],1,0);
link(id[u][v][1],id[u][v][0],1,1);
link(id[u][v][2],id[u][v][0],1,0);
link(id[u][v][2],id[u][v][0],1,1);
}
}
if((u+v)%2==0)
{
int x,y;
R(i,0,3)
{
x=u+dx[i],y=v+dy[i];
if(x<0||y<0||x>=n||y>=m) continue;
if(field[x][y]=='w') continue;
//printf("x:%d y:%d\n",x,y);
//cout<<"FA"<<field[x][y]<<endl;
//printf("i:%d id:%d id:%d\n",i,id[u][v][i%2+1],id[x][y][i%2+1]);
link(id[u][v][i%2+1],id[x][y][i%2+1],1,0);
}
}
}
void spfa()
{
deque<int>q;
R(i,0,3020) h[i]=INF,vis[i]=0;
//memset(h,0x3f,sizeof(h));
h[s]=0;vis[s]=1;
q.pb(s);int u,v;
while((int)q.size()>0)
{
u=q.front();q.pop_front();
vis[u]=0;
for(int i=head[u];i;i=e[i].nxt)
{
v=e[i].to;
if(e[i].cap&&h[v]>h[u]+e[i].cos)
{
h[v]=h[u]+e[i].cos;
if(!vis[v]) vis[v]=1,q.pb(v);
}
}
}
}
struct node
{
int val,pos;
inline int operator <(const node &A)const {return val>A.val;}
};
pii p[50010];
int dij()
{
priority_queue<node>q;
R(i,0,3030) dis[i]=INF,vis[i]=0;
//memset(dis,0x3f,sizeof(dis));
//memset(vis,0,sizeof(vis));
dis[s]=0;
q.push((node){0,s});
int u,v,tc;
while((int)q.size()>0)
{
u=q.top().pos,q.pop();
if(vis[u]) continue;vis[u]=1;
for(int i=head[u];i;i=e[i].nxt)
{
v=e[i].to;tc=e[i].cos+h[u]-h[v];
if(e[i].cap&&dis[v]>dis[u]+tc)
{
dis[v]=dis[u]+tc;
p[v]=mkp(u,i);
if(!vis[v]) q.push((node){dis[v],v});
}
}
}
return dis[t]<INF;
}
void MCMF()
{
int minF;
spfa();
while(dij())
{
minF=INF;
R(i,0,3030) h[i]+=dis[i];
for(int i=t;i^s;i=p[i].fi) ckmin(minF,e[p[i].se].cap);
for(int i=t;i^s;i=p[i].fi) e[p[i].se].cap-=minF,e[p[i].se^1].cap+=minF;
MXF+=minF,MNC+=minF*h[t];
}
}
struct CurvyonRails
{
inline int getmin(vector<string> field)
{
n=(int)field.size(),m=(int)field[0].size();
::field=field;
R(i,0,n-1) R(j,0,m-1)
{
id[i][j][0]=i*m+j;
id[i][j][1]=i*m+n*m+j;
id[i][j][2]=i*m+2*n*m+j;
}
s=n*m*3,t=s+1;
int sumf=0;
R(i,0,n-1) R(j,0,m-1)
{
if(field[i][j]=='w') continue;
if((i+j)%2==0) sumf+=2;
if(field[i][j]=='.') Add(i,j,0);
if(field[i][j]=='C') Add(i,j,1);
}
MCMF();
//printf("mf:%d llf:%d\n",MXF,sumf);
if(MXF<sumf) return -1;
return MNC;
}
};
/*
signed main()
{
//freopen("cxytxdy.in","r",stdin);
string tmp;
vector<string>field;
int n;
cin>>n;
R(i,1,n) cin>>tmp,field.pb(tmp);
CurvyonRails mian;
writeln(mian.getmin(field));
}
*/
无源汇上下界可行流
在一个没有源汇的图中,每条边都有一个流量的上界和下界,我们需要求一个可行流,使它的出入是平衡的,而且每条边的流量就在这个界中。
考虑先将每条边的下界的流量流完,然后将流入大于流出的点和流出大于流入的点分开,新建源点汇点。对于流入大于流出的点,假设流入比流出大\(x\),那么加入边\((s,i,x)\)表示从\(s\)到\(i\),流量为\(x\)。对于流出大于流入的点,加入\((i,t,x)\)。然后对于原来的边\((x,y,u,d)\),\(u\)指上界,\(d\)指下界,加入边\((x,y,u-d)\)。判断新图是否满流即可。
const int N=222222;
int n,m,s,t,sumf;
int dis[N],ind[N],oud[N],now[N],lst[N];
int head[N],cnt_e=1;
struct edge {int nxt,to,cap;}e[N<<1];
int flow[N<<1];
inline void add_edge(int u,int v,int f)
{
e[++cnt_e]=(edge){head[u],v,f},head[u]=cnt_e,flow[cnt_e]=0;
}
inline void link(int u,int v,int f)
{
add_edge(u,v,f),add_edge(v,u,0);return;
}
deque<int>q;
int bfs()
{
memset(dis,0,sizeof(dis));
q.clear();
q.pb(s);
dis[s]=1;
int u,v;
while((int)q.size()>0)
{
u=q.front();q.pop_front();
for(int i=head[u];i;i=e[i].nxt)
{
v=e[i].to;
if(dis[v]||flow[i]==e[i].cap) continue;
dis[v]=dis[u]+1;
q.pb(v);
}
}
return dis[t]>0;
}
int dfs(int u,int mc)
{
if(u==t) return mc;
int res=0,v,k;
for(int i=now[u];i&&res<mc;i=e[i].nxt)
{
v=e[i].to;
if(flow[i]==e[i].cap||dis[v]!=dis[u]+1) continue;
k=dfs(v,min(mc-res,e[i].cap-flow[i]));
flow[i]+=k,flow[i^1]-=k,res+=k;
}
return res;
}
int dinic()
{
int res=0;
while(bfs())
{
R(i,1,t) now[i]=head[i];
res+=dfs(s,inf);
}
return res;
}
signed main()
{
n=read(),m=read();
s=n+1,t=s+1;
int x,y,u,d;
R(i,1,m)
{
x=read(),y=read(),d=read(),u=read();
ind[y]+=d,oud[x]+=d,lst[i]=d;
link(x,y,u-d);
}
R(i,1,n)
{
if(ind[i]<oud[i]) link(i,t,oud[i]-ind[i]);
if(ind[i]>oud[i]) link(s,i,ind[i]-oud[i]);
sumf+=abs(ind[i]-oud[i]);
}
sumf>>=1;
int res=dinic();
if(res<sumf) return puts("NO")&0;
puts("YES");
R(i,1,m) writeln(flow[i<<1]+lst[i]);
}
有源汇上下界最大流
还是先把每条边的下界流量先流完,类似地判断一下合不合法,由于源点和汇点流量不一定需要平衡,直接连一条边\((t,s,inf)\)即可。然后将新建的源点和汇点删掉。然后再在残余网络上跑一遍\(s\to t\)的最大流即可。
const int N=30030;
int n,m,s,t,ns,nt,sumf;
int dis[N],ind[N],oud[N],now[N];
int head[N],cnt_e=1,flow[N<<1];
struct edge {int nxt,to,cap;}e[N<<1];
inline void add_edge(int u,int v,int f)
{
e[++cnt_e]=(edge){head[u],v,f};head[u]=cnt_e;flow[cnt_e]=0;
}
inline void link(int u,int v,int f)
{
add_edge(u,v,f),add_edge(v,u,0);
}
deque<int>q;
int bfs()
{
memset(dis,0,sizeof(dis));
q.clear();
q.pb(s);
dis[s]=1;
int u,v;
while((int)q.size()>0)
{
u=q.front();q.pop_front();
for(int i=head[u];i;i=e[i].nxt)
{
v=e[i].to;
if(dis[v]||flow[i]==e[i].cap) continue;
dis[v]=dis[u]+1;
q.pb(v);
}
}
return (dis[t]>0);
}
int dfs(int u,int mc)
{
if(u==t) return mc;
int res=0,v,k;
for(int i=now[u];i&&res<mc;i=e[i].nxt)
{
v=e[i].to;
if(flow[i]==e[i].cap||dis[v]!=dis[u]+1) continue;
k=dfs(v,min(mc-res,e[i].cap-flow[i]));
flow[i]+=k,flow[i^1]-=k,res+=k;
}
return res;
}
int dinic()
{
int res=0;
while(bfs())
{
//test
cpy(now,head,t+5);
//R(i,1,t) now[i]=head[i];
res+=dfs(s,inf);
}
return res;
}
signed main()
{
n=read(),m=read(),ns=read(),nt=read(),s=n+1,t=s+1;
int x,y,u,d;
R(i,1,m)
{
x=read(),y=read(),d=read(),u=read();
ind[y]+=d,oud[x]+=d;link(x,y,u-d);
}
link(nt,ns,inf);
int tmp=cnt_e-1;
R(i,1,n)
{
if(ind[i]<oud[i]) link(i,t,oud[i]-ind[i]);
if(ind[i]>oud[i]) link(s,i,ind[i]-oud[i]);
sumf+=abs(ind[i]-oud[i]);
}
sumf>>=1;
int res=dinic();
if(res<sumf) return puts("please go home to sleep")&0;
else
{
res=flow[tmp];
e[tmp].cap=flow[tmp]=flow[tmp^1]=0;
s=ns,t=nt;
res+=dinic();
writeln(res);
}
}
有源汇上下界最小流
求出一组可行流后求从\(t\)到\(s\)的最大流。然后把可行流的流量减去它即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号