构造
UOJ460
一个\(n\)个点的完全图,你需要从中选出尽量多的不交的生成树。
\(n\leq 1000\)
uoj460
首先分析出上界显然是\(\frac{n(n-1)}{2(n-1)}=\lfloor \frac{n}{2} \rfloor\)
归纳构造,假设\(n=2k\)时已经构造好了,考虑\(n=2k+1\)。
显然由于每个点都存在于每棵树中,随便选\(k\)个不同的点(每个点对应一棵树)连上新加的点就行。
考虑\(n=2k+2\)。
类似的,我们先选\(1\sim k\)这些点连上\(2k+1\),\(k+1\sim 2k\)这些点连上\(2k+2\),这样就先成功把之前的\(k\)棵树都加上新加的两个点。
接下来做一棵新的树,让\(2k+2\)连向\(1\sim k\),\(2k+1\)连向\(k+1\sim 2k\),然后\(2k+1,2k+2\)连一条边即可。
int n;
vector<pii>e[2222];
signed main()
{
n=read();
for(int i=2;i<=n;i+=2)
{
static int t,p;
t=(i-2)/2,p=t+1;
R(j,1,t)
{
e[j].pb(mkp(j,i-1));
e[j].pb(mkp(j+t,i));
}
R(j,1,t)
{
e[p].pb(mkp(j,i));
e[p].pb(mkp(j+t,i-1));
}
e[p].pb(mkp(i-1,i));
}
if(n&1) R(i,1,n>>1) e[i].pb(mkp(i,n));
writeln(n>>1);
R(i,1,n>>1)
{
for(pii qwq:e[i]) printf("%d %d ",qwq.fi,qwq.se);puts("");
}
}
NFLSPC #3 G
平面上有\(n\)个蓝色的点,你需要加上\(k\)个红色的点,使得任意三个蓝点组成的三角形内部都必须至少有一个红点。注意红点必须在三角形内部,不能在边上。
你需要最小化\(k\)的大小。
\(n\leq 100\)。
引理:答案为\(2n-2 -\) 凸包上的点数。
首先证明这是答案的下界。设最外层凸包点数为\(l_1\),把这些点去掉,对于剩余的点再求一次凸包得到第二层凸包点数\(l_2\)……以此类推,我们可以把这些点划分成\(k\)个互相包含的凸包,点数分别为\(l_1,l_2,\ldots ,l_k\)。
对于相邻两层凸包之间的部分进行三角剖分,可以得到\(l_i+l_{i+1}\)个三角形,最里面的凸包直接三角剖分,因此总共有\((l_1+l_2)+(l_2+l_3)+\ldots +(l_{k-1}+l_k)+(l_k-2)=2n-2-l_1\)个三角形,这些三角形两两没有交,因此这是答案的下界。
其次存在一个构造可以达到这个下界。
随机一个向量\(p\),使得任意两个蓝点构成的向量不与\(p\)平行,令\(|p|\to 0\),同时在每个点\(+p\)和\(-p\)位置点,可以证明这\(2n\)个点满足要求。
这是因为把一个三角形的三个角平移到一起刚好可以覆盖\(180\)度,根据抽屉原理,必然有一个点落在这里。
但是\(2n\)个点多了,我们把所有在凸包外面的红点删掉(注意凸包最两侧的点可以删掉\(2\)个红点),因此剩余的总点数恰好为\(2n-2-\) 凸包点数。
证毕。
上述引理的证明过程也给出了构造。
struct point
{
int x,y;
inline point(int X = 0,int Y = 0): x(X), y(Y) {}
inline int operator <(const point &A)const
{
return x^A.x?x<A.x:y<A.y;
}
inline point operator -(const point &A)const
{
return point(x-A.x,y-A.y);
}
}p[111],lww[111],upp[111],cov[222];
int tpl,tpr,all;
set<point>st;
inline int times(const point &A,const point &B){return A.x*B.y-A.y*B.x;}
int n;
inline int gcd(int a,int b){return !b?a:gcd(b,a%b);}
signed main()
{
n=read();
int x,y;
R(i,1,n) x=read(),y=read(),p[i]=point(x,y);
sort(p+1,p+n+1);
R(i,1,n) R(j,i+1,n)
{
static int x,y,g;
x=abs(p[j].x-p[i].x),y=abs(p[j].y-p[i].y),g=gcd(x,y);
assert(g>=1);
x/=g,y/=g;
st.insert(point(x,y));
}
int ok=0;
point lam;
R(i,1,1000)
{
R(j,1,1000) if(gcd(i,j)==1&&st.find(point(i,j))==st.end())
{
ok=1;
lam=point(i,j);
break;
}
if(ok) break;
}
st.clear();
R(i,1,n)
{
while(tpl>=2&×(lww[tpl]-lww[tpl-1],p[i]-lww[tpl])<=0) tpl--;
lww[++tpl]=p[i];
}
L(i,1,n)
{
while(tpr>=2&×(upp[tpr]-upp[tpr-1],p[i]-upp[tpr])<=0) tpr--;
upp[++tpr]=p[i];
}
R(i,1,tpl) cov[++all]=lww[i],st.insert(lww[i]);
R(i,2,tpr-1) cov[++all]=upp[i],st.insert(upp[i]);
printf("%lld\n",2ll*n-all-2);
double disl=sqrt(lam.x*lam.x+lam.y*lam.y);
double dx=lam.x/disl*1e-5,dy=lam.y/disl*1e-5;
R(i,1,n) if(st.find(p[i])==st.end())
{
printf("%.10lf %.10lf\n",p[i].x+dx,p[i].y+dy);
printf("%.10lf %.10lf\n",p[i].x-dx,p[i].y-dy);
}
cov[0]=cov[all];
cov[all+1]=cov[1];
point mal(-lam.x,-lam.y);
R(i,1,all)
{
static point pre,now,nxt;
pre=cov[i-1],now=cov[i],nxt=cov[i+1];
if(times(nxt-now,lam)>0&×(pre-now,lam)<0) printf("%.10lf %.10lf\n",now.x+dx,now.y+dy);
if(times(nxt-now,mal)>0&×(pre-now,mal)<0) printf("%.10lf %.10lf\n",now.x-dx,now.y-dy);
}
}
NFLSPC #2 C
一个\(n\times n\)的方格表,每个格子里有个字母。
每次可以把某一行所有字母向右循环平移若干格,或者把某列所有字母向下循环平移若干格。
若某行连续的三个字母为\(k,e,y\),则成为一个“键”。
你需要在\(10000\)次操作内,最大化键的数量。
\(n\leq 40\)
如果让自己随便写一个矩阵让\(key\)尽量多,那显然每行都应该是\(keykeykey\ldots\)的形式。如果列数不是\(3\)的倍数,就会多出来一两个不能形成\(key\)的列。
考虑一列一列进行操作,考虑假设前\(i-1\)列已经是\(keykey\ldots\)的形式了,当前要把第\(i\)列弄成全部为\(k\)的。随便找到右边的一个\(k\),然后找到第\(i\)列某个还不是\(k\)的行\(j\),把第\(j\)行先右移出来,然后把\(k\)塞进去,再把第\(j\)行左移回去即可。
注意一下如果这一列的\(k\)填不满,我们还需要把不是\(e,y\)的字符挪进来。如果剩下的字符已经全是\(e,y\)了,那么计算一下右边在最优策略下\(e,y\)分别会使用多少,把不使用的填进来即可。
若列数不为\(3\)的倍数,显然最后一列不需要管;如果是\(3\)的倍数,注意到剩下的字符自然而然会全出现在最后一行,但是顺序不一定一致。考虑如何调整最后一列的顺序。
注意到如果倒数第二列全是\(e\)或者最后一列全是\(y\),我们完全没有必要调整最后一列。否则倒数第二列一定有一个不是\(e\)的位置,记这一行为\(x\)。同时最后一列也一定有一个不是\(y\)的位置。
事实上这种情况下显然可以交换最后一列任意两个位置\(a,b\)。
先把\(a\)挪到第\(x\)行,然后向右移一行,将\(b\)上挪到第\(x\)行,在左移,此时\(a\)到了\(b\)的位置上。接着再把\(a\)下移到这一列回去,然后再把第\(x\)行右移回去,此时\(a,b\)的位置都交换了。
但是此时第\(x\)行本来的元素整体右移了一格,由于最后一列有个不是\(y\)的位置,把这个位置挪到\(x\)行然后左移即可。
因此可以\(O(n^2)\)次操作使得只剩最后一列需要调整,再花\(O(n)\)次操作可以调整好最后一列。
int n;
char s[44][44];
char t[44][44];
map<char,int>cnt;
int mx_ans,mxj;
char tmp[22222];
int vis[44][44];
vector<pair<int,pii> >ans;
void solve(int x,int y,int z)
{
z=(z%n+n)%n;
if(!z) return;
ans.pb(mkp(x,mkp(y,z)));
if(!x)
{
R(i,1,n) tmp[(i-1+z)%n+1]=s[y][i];
R(i,1,n) s[y][i]=tmp[i];
}
if(x==1)
{
R(i,1,n) tmp[(i-1+z)%n+1]=s[i][y];
R(i,1,n) s[i][y]=tmp[i];
}
}
signed main()
{
n=read();
if(n<=2) return puts("0")&0;
R(i,1,n)
{
scanf("%s",s[i]+1);
R(j,1,n) ++cnt[s[i][j]];
}
mxj=inf;
ckmin(mxj,cnt['k']),ckmin(mxj,cnt['e']),ckmin(mxj,cnt['y']),ckmin(mxj,n/3*n);
int tmpmx=mxj;
cnt['k']-=mxj,cnt['e']-=mxj,cnt['y']-=mxj;
for(int j=n-2;j>=1&&tmpmx;j-=3)
{
for(int i=n;i>=1&&tmpmx;i--) t[i][j]='k',t[i][j+1]='e',t[i][j+2]='y',--tmpmx;
}
int all=0;
R(i,1,127) while(cnt[i]--) tmp[++all]=i;
R(i,1,n) R(j,1,n) if(!t[i][j]) t[i][j]=tmp[all--];
R(j,1,n-1)
{
R(i,1,n)
{
static int x,y,ok;
y=n,ok=0;
for(;y>=j;y--)
{
for(x=1;x<=n;x++)
if(!vis[x][y]&&s[x][y]==t[i][j]) {ok=1;break;}
if(ok) break;
}
if(i!=1)
{
if(y==j)
{
solve(0,x,1);
solve(1,j+1,1-x);
solve(0,x,-1);
x=1,y=j+1;
}
solve(1,y,1-x);
solve(0,1,j-y);
solve(1,j,-1);
solve(0,1,y-j);
vis[n+2-i][j]=1;
}
else
{
if(y==j) solve(1,j,1-x);
if(y>j)
{
solve(1,y,2-x);
solve(0,2,j-y);
solve(1,j,-1);
solve(0,2,y-j);
}
vis[i][j]=1;
}
}
}
if(mxj<n)
{
R(i,1,n)
{
if(s[1][n]=='y') solve(0,1,-1);
solve(1,n,1);
}
R(i,1,mxj) solve(0,1,1),solve(1,n,-1);
}
writeln((int)ans.size());
for(auto qwq:ans) printf("%d %d %d\n",qwq.fi,qwq.se.fi,qwq.se.se);
}
CF1375H
有一个排列\(a_1,\cdots a_n\),\(n\)个集合初始分别为\(\{a_1\},\{a_2\},\cdots ,\{a_n\}\),每次可以合并两个集合得到新的集合(原来两个集合仍然保留),条件是其中一个集合的最大值小于另一个集合的最小值(即值域区间不交)。
给定\(Q\)组\(l_i,r_i\),你需要在\(2.2\times 10^6\)次操作内合并出一些集合,使得每组\(\{a_{l_i},\ldots a_{r_i}\}\)存在于这些集合之中。
\(n\leq 2^{12},Q\leq 2^{16}\)
显然分块,由于合并集合对于值域的限制很强,因此采用值域分块。
于是每次询问就变成了把每一块内下标在\([l_i,r_i]\)之间的连续段提取出来然后合并。
于是问题就变成了如何算出一块中所有连续段对应的集合。
考虑继续值域分治,每次合并之后连续段对应两边的某个连续段,直接合并即可。
复杂度是\(T(n)=2T(\frac{n}{2})+O(n^2)=O(n^2)\),设块大小为\(B\),预处理的时间复杂度就是\(O(nB)\),询问的复杂度是\(O(\frac{Qn}{B})\),因此\(B=\sqrt {Q}=2^8\)时最优。
int n,m;
int a[4444];
int ans[66666],pos[4444];
const int B=1<<8;
int tot_b;
pii id[8888888];
int mer(int x,int y)
{
if(!x||!y) return x|y;
id[tot_b]=mkp(x,y);
return ++tot_b;
}
struct node
{
vector<int>val;
vector<vector<int>>id;
inline void init(int x)
{
val.resize(x),id.resize(x);
R(i,0,x-1) id[i].resize(x-i);
}
node(int opt=-1){if(~opt)init(1),val[0]=pos[opt],id[0][0]=pos[opt]+1;}
inline int query(int l,int r)const
{
if(r<val.front()||l>val.back()) return 0;
int L=lower_bound(val.begin(),val.end(),l)-val.begin(),R=upper_bound(val.begin(),val.end(),r)-val.begin()-1;
return L>R?0:id[L][R-L];
}
inline node modify(const node &a,const node &b)
{
init(a.val.size()+b.val.size());
merge(a.val.begin(),a.val.end(),b.val.begin(),b.val.end(),val.begin());
R(i,0,(int)val.size()-1) R(j,i,(int)val.size()-1) id[i][j-i]=mer(a.query(val[i],val[j]),b.query(val[i],val[j]));
return *this;
}
}b[2222];
node solve(int l,int r)
{
if(l==r) return node(l);
int mid=(l+r)>>1;
static node tmp;
return tmp.modify(solve(l,mid),solve(mid+1,r));
}
signed main()
{
n=read()-1,m=read(),tot_b=n+1;
R(i,0,n) a[i]=read()-1,pos[a[i]]=i;
R(i,0,n/B) b[i]=solve(i*B,min(n,(i+1)*B-1));
int l,r;
R(t,0,m-1)
{
l=read()-1,r=read()-1;
R(j,0,n/B) ans[t]=mer(ans[t],b[j].query(l,r));
}
writeln(tot_b);
R(i,n+1,tot_b-1) printf("%lld %lld\n",id[i].fi,id[i].se);
R(i,0,m-1) writesp(ans[i]);
}
CF1364E
给定一个\([0,n-1]\)排列\(P\),每次询问\((i,j),i\neq j\)返回\(p_i|p_j\),最多\(4269\)次询问,推出这个排列。
\(n\leq 2048\)
显然如果知道了\(0\)的位置,那么就直接做完了。
怎么得到\(0\)的位置呢?
做法\(1\):我们随便选择一个数字,让它或上所有的其他数,显然\(0\)和它或起来必然是一个最小值。
于是再把所有最小值拿出来,从中随机一个数字再和其它所有数或取值为最小值的……每次二进制中\(1\)的个数期望减半,因此大约是\(O(n+\sqrt n +\ldots)\)。
但是事实总是不尽人意,这种做法需要卡常卡半天才能过。
具体做法是每次让它真的减半而不是期望减半,考虑新随机一个数,算一下这个数字与其他某5个数字的或,如果这5个数字的\(1\)的个数都比较多,就重新随一个数。
做法2:这是一个严格线性的做法。
考虑从左往右扫,当前维护了两个位置\(a,b\)表示前缀中的\(0\)只可能出现在\(a,b\)中。设当前位置的数字为\(c\),则:
- \(a|c>a|b\),则\(c\)必然不是\(0\)。
- \(a|c<a|b\),则\(b\)必然不是\(0\)。
- \(a|c=a|b\),则\(a\)必然不是\(0\)。
上述做法看上去是\(2n\)的,但是注意到需要更新\(a|b\)值的时候只有\(2,3\)两种情况,并且由于\(a|c\)是必然要问的,因此第二种情况不需要额外花费,只有第三种情况需要额外花费。
但是随机情况下第三种情况发生的概率事实上很低,因此可以random_shuffle之后做。
于是最后问题变成了从两个数里挑一个是\(0\),这个可以从其它数里random一个出来,和它们两个分别或,如果或出来不一样,显然\(0\)就出来了。
int n;
int ans[2222],id[2222];
map<int,int>mp[2222];
inline int query1(int a,int b)
{
if(a>b) swap(a,b);
if(mp[a][b]) return mp[a][b];
cout<<"? "<<a<<" "<<b<<endl;
fflush(stdout);
static int tmp;
cin>>tmp;fflush(stdout);
return mp[a][b]=tmp;
}
inline void print(int pos0)
{
R(i,1,n) if(i==pos0) ans[i]=0;else ans[i]=query1(pos0,i);
cout<<"! ";R(i,1,n) cout<<ans[i]<<" ";cout<<endl;fflush(stdout);
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
srand(time(0));
cin>>n;
R(i,1,n) id[i]=i;
R(i,2,n) swap(id[i],id[1ll*rand()*rand()%i+1]);
int A=id[1],B=id[2],val=query1(A,B),pos0=A;
R(i,3,n)
{
static int tmp;
tmp=query1(A,id[i]);
if(tmp<val) B=id[i],val=query1(A,B);
else if(tmp==val) A=id[i],val=query1(A,B);
}
while(1)
{
static int t,vl1,vl2;
t=1ll*rand()*rand()%n+1;
if(t==A||t==B) continue;
vl1=query1(A,t),vl2=query1(B,t);
if(vl1^vl2)
{
if(vl1>vl2) pos0=B;
else pos0=A;
break;
}
}
print(pos0);
}
CF1365G
有一个数组\(A\),你可以每次询问一些位置,会告诉你这些位置上数字的或。
你需要在\(13\)次操作内得到所有的\(P_i\)表示除了\(A_i\)以外其它所有数字的按位或。
\(n\leq 1000\)
20次的做法:
每一个位置都对应了一个二进制数,将每一个位置的二进制数写下来。
然后将第一位为\(1\)的二进制数全拿出来然后算一个或,将第一位为\(0\)的二进制数全拿出来算一个或。然后对于每一位都这么处理,由于\(n=1000<2^{10}\)所以总共需\(20\)次。
对于某一个位置,取出二进制下每一位取反的数的答案或起来即可。
考虑一种全新的方法:将所有\(13\)位的,且恰好有\(6\)个\(1\)的二进制数拿出来,和题目中给定的\(n\)个数做映射,由于\(\binom {13} 6>1000\)因此肯定可以构成满射。
枚举\(13\)位中的某一位,把所有这一位上为\(1\)的二进制数拿出来,把它们对应的数列中的数字算个按位或,记为\(W_k\)。
此时,对于一个位置\(i\),除了它以外的所有数字的按位或就是它对应的二进制数中,所有\(0\)位对应的\(W_k\)或起来。这是因为保证了\(1\)的个数都相同。
int n;
int cnt[1111111];
vector<int>v;
int ans[22];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n;fflush(stdout);
R(mask,1,1<<13)
{
cnt[mask]=cnt[mask>>1]+(mask&1);
if(cnt[mask]!=6) continue;
v.pb(mask);
if((int)v.size()==n) break;
}
R(i,0,12)
{
static int tmp;tmp=0;
R(j,0,(int)v.size()-1) if(v[j]&(1<<i)) tmp++;
if(!tmp) continue;
cout<<"? "<<tmp<<" ";
R(j,0,(int)v.size()-1) if(v[j]&(1<<i)) cout<<j+1<<" ";
cout<<endl;fflush(stdout);
cin>>ans[i];fflush(stdout);
}
cout<<"! ";
R(i,0,(int)v.size()-1)
{
static int tmp;
tmp=0;
R(j,0,12) if(!(v[i]&(1<<j))) tmp|=ans[j];
cout<<tmp<<" ";
}
cout<<endl;fflush(stdout);
}
CF1290D
有一个长度为\(n\)的未知序列\(a\)和一个大小为\(k\)的队列\(S\)。保证\(1\leq k\leq n\leq 1024\),且\(n,k\)都是2的次幂。
你可以进行一下两种操作:
- 询问:选择一个数\(i(1\leq i\leq n)\),并输出
? i- 交互程序会检查\(S\)中是否包含\(a_i\),是则输出
Y,否则输出N - 然后将\(a_i\)加入队尾,若\(|S|\ge k\),则弹出队首。
- 交互程序会检查\(S\)中是否包含\(a_i\),是则输出
- 重置:输出
R,交互程序会清空队列。
保证\(\frac{3n^2}{2k}\leq 15000\)
你需要在不超过\(\frac{3n^2}{2k}\)次询问和不超过\(30000\)次重置之内得出序列\(a\)中不同数的数量\(d\),并输出! d
事实上只要算出每个数字是否在之前出现过即可。
显然直接分块,每\(\frac{k}{2}\)一块,每次跳两个块出来扔到队列里加一遍。但操作次数是\(\frac{2n^2}{k}\)的,不能够通过。
枚举\(i=1\ldots \frac{2n}{k}\),每次把间隔为\(i\)的块依次加入队列。
注意\(i>\frac{n}{k}\)时,有些块就不需要被加入队列了,这些块的数量大致构成了一个等差数列,因此会有\(\frac{1}{2}\)的常数。
这样常数之和恰好为\(\frac{3}{2}\),可以通过本题。
然而还有更强的\(\frac{n^2}{k}\)做法。
int n,k,totB;
int vis[1111];
inline int query(int x)
{
cout<<"? "<<x<<endl;fflush(stdout);
static char tmp;
cin>>tmp;
return (tmp=='Y');
}
inline void clear()
{
cout<<"R"<<endl;fflush(stdout);
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>k;totB=n/k;
fill(vis,vis+n+5,1);
R(i,1,totB)
{
clear();
static int d;d=0;
R(j,1,totB)
{
static int t;
t=i+d;
while(t<=0) t+=totB;
while(t>totB) t-=totB;
R(z,(t-1)*k+1,t*k) if(vis[z]&&query(z)) vis[z]=0;
if(d>=0) ++d;d=-d;
}
}
int ans=0;
R(i,1,n) ans+=vis[i];
cout<<"! "<<ans<<endl;fflush(stdout);
}
CF1292E
一个长度为\(n\)的字符串\(S\),只包含\(C,H,O\)三个字母,你每次可以询问一个字符串\(p\),交互库会告诉你\(p\)作为\(S\)的子串出现的开头位置是哪些。
假设\(p\)的长度为\(t\),那么这次询问的代价是\(\frac{1}{t^2}\)。你需要在总代价为\(\frac{7}{5}\)内询问出字符串\(S\)。
\(4\leq n\leq 50\)。
最暴力的做法肯定是直接花费\(2\)问\(C,O\),剩下的位置就是\(H\)。
但是这种做法给了我们一些启发,事实上可以稍微加长一下询问的串长。
我们询问\(CC,CH,CO,HO,OO\),即询问过后我们知道了所有\(C\)后面的字符和\(O\)前面的字符。对于没确定的位置,它要么是最后一位或者第一位,要么必然是\(H\)。
因此只有最后一位或者第一位需要单独枚举判断,最后一位只可能是\(C,H\),第一位只可能是\(O,H\),因此再进行三次长度为\(n\)的询问即可。
但是这只在\(n>4\)的时候可以成功,\(n=4\)时\(1.25+\frac{3}{16}>1.4\)。
一部分难点在于\(n=4\)的处理。
\(n=4\)时,肯定不能最先开始大手大脚花掉\(5\)次长度为\(2\)的询问了,考虑减少一点,只问\(CC,CH,CO\)。
注意如果\(1,2,3\)位中有\(C\),那么显然已经出来了,并且它的后一位也就出来了。此时就只有两位不确定,其中一位必然不是最后一个因此只有两种可能(不可能是\(C\)),因此最多有\(6\)种情况,问\(5\)次即可确定。此时\(\frac{3}{4}+\frac{5}{16}<1.4\)。
否则\(1,2,3\)位就都不是\(C\),此时再问\(HO\),如果有东西被问出来了,那么仍然至多是\(1+\frac{5}{16}<1.4\)(最后一位仍然是不定的),如果没有东西被问出来,我们再问\(OO\),此时如果还是没东西出来,那就说明\(2,3,4\)没有\(O\),即\(2,3\)两位是\(H\),问下\(HHH\)就知道第一位以及最后一位是不是\(H\)了,这里花费\(1.25+\frac{1}{9}<1.4\)。
如果出现了\(OO\),并且在\(3,4\),那就说明\(2\)位置是\(H\),此时只剩下\(1\)位置不定,问一下即可。如果在\(2,3\),那么就说明\(1\)位置必然不是\(O\),于是也只需要问一下就行。这里代价是\(1.25+\frac{1}{16}<1.4\)。
int n,sl;
char s[55],t[55];
inline int query()
{
s[sl+1]='\0';
cout<<"? "<<s+1<<endl;cout.flush();
static int k,a;
cin>>k;if(k<0) exit(0);cout.flush();
R(i,1,k)
{
cin>>a;cout.flush();
R(j,1,sl) t[a+j-1]=s[j];
}
return k;
}
inline void print()
{
t[n+1]='\0';
cout<<"! "<<t+1<<endl;cout.flush();
static int _;cin>>_;cout.flush();
if(!_) exit(0);
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int _;cin>>_;cout.flush();
for(;_--;)
{
cin>>n;cout.flush();
if(n>4)
{
sl=2;
s[1]='C',s[2]='C';query();
s[1]='C',s[2]='H';query();
s[1]='C',s[2]='O';query();
s[1]='H',s[2]='O';query();
s[1]='O',s[2]='O';query();
R(i,2,n-1) if(!t[i]) t[i]='H';
sl=n;
R(i,2,n-1) s[i]=t[i];s[1]=t[1]?t[1]:'O';s[n]=t[n]?t[n]:'C';query();
R(i,2,n-1) s[i]=t[i];s[1]=t[1]?t[1]:'O';s[n]=t[n]?t[n]:'H';query();
R(i,2,n-1) s[i]=t[i];s[1]=t[1]?t[1]:'H';s[n]=t[n]?t[n]:'C';query();
R(i,2,n-1) s[i]=t[i];t[1]=t[1]?t[1]:'H',t[n]=t[n]?t[n]:'H';
}
else
{
sl=2;
s[1]='C',s[2]='C';query();
s[1]='C',s[2]='H';query();
s[1]='C',s[2]='O';query();
s[1]='H',s[2]='O';query();
if(!t[1]&&t[2]&&t[3]&&!t[4])
{
sl=n;
R(i,2,n-1) s[i]=t[i];s[1]=t[1]?t[1]:'H';s[n]=t[n]?t[n]:'C';query();
R(i,2,n-1) s[i]=t[i];s[1]=t[1]?t[1]:'H';s[n]=t[n]?t[n]:'H';query();
R(i,2,n-1) s[i]=t[i];s[1]=t[1]?t[1]:'H';s[n]=t[n]?t[n]:'O';query();
R(i,2,n-1) s[i]=t[i];s[1]=t[1]?t[1]:'O';s[n]=t[n]?t[n]:'C';query();
R(i,2,n-1) s[i]=t[i];s[1]=t[1]?t[1]:'O';s[n]=t[n]?t[n]:'H';query();
R(i,2,n-1) s[i]=t[i];
t[1]=t[1]?t[1]:'O',t[n]=t[n]?t[n]:'O';
}
else
{
s[1]='O',s[2]='O',query();
t[2]=t[2]?t[2]:'H',t[3]=t[3]?t[3]:'H';
if(t[2]=='H'&&t[3]=='H')
{
sl=3;
s[1]='H',s[2]='H',s[3]='H';
query();
t[1]=t[1]?t[1]:'O',t[4]=t[4]?t[4]:'C';
}
else
{
sl=4;
if(!t[1])
{
R(i,2,4)s[i]=t[i];s[1]='H';query();
R(i,2,4)s[i]=t[i];s[1]='O';query();
}
else
{
R(i,1,3)s[i]=t[i];s[4]='C';query();
R(i,1,3)s[i]=t[i];s[4]='H';query();
}
}
}
}
print();
R(i,0,n+5) t[i]='\0';
}
}
CF1288F
一张二分图,左边\(n_1\)个点,右边\(n_2\)个点,总共\(m\)条边,每个点有个颜色\(R,B\),或者没有颜色(记为\(U\)),现在需要给边染色,染成\(R\)需要花费\(r\)的代价,染成\(B\)需要花费\(b\)的代价。
要求对于每个颜色为\(R\)的点,与之相邻的边中颜色为\(R\)的边严格多于颜色为\(B\)的边,对于颜色为\(B\)的点类似。求花费最小的方案,无解输出\(-1\)。
边可以不染色。
\(n_1,n_2,m\leq 200\)。
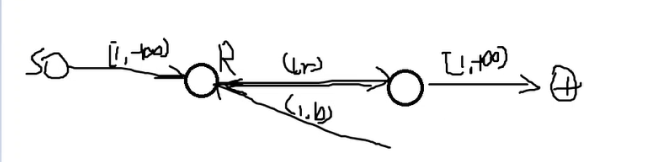
这是个长得像构造的上下界费用流题。
基本思想上直接二分图建图,如果这条边的颜色为\(R\),就钦定往右边流,否则如果是\(B\)就往左边流。
那么对于一个点\(R\),就要严格要求流进它的边要严格小于流出它的边。
因此考虑直接从源点向它连一条\([1,+\infty]\)的边,这样就可以保证从它流出的流量大于流进它的流量了。
若左边的点为\(B\),则从它向\(T\)连下界为\(1\),上界无穷大,费用为\(0\)的边;
若左边的点为\(U\),则\(S\)向它、它向\(T\)都连上界无穷大,费用为\(0\)的边。
若右边的点为\(R\),则从它向\(T\)连下界为\(1\),上界无穷大,费用为\(0\)的边;
若右边的点为\(B\),则从\(S\)向它连下界为\(1\),上界无穷大,费用为\(0\)的边;
若右边的点为\(U\),则\(S\)向它,它向\(T\)都连上界无穷大,费用为\(0\)的边。
对于原图中的边,连\((u,v,1,r)\)和\((v,u,1,b)\)。
直接跑最小费用上下界可行流即可。
int n1,n2,m,cstr,cstb;
int s,t,S,T;
char str[2222];
struct edge
{
int nxt,to,cap,cst;
}e[88888];
int ind[4444],oud[4444],dis[4444],flow[88888],vis[4444];
int head[4444],now[4444],cnt_e=1;
int idr[2222],idb[2222];
int sumf;
inline void add_edge(int u,int v,int d,int c)
{
e[++cnt_e]=(edge){head[u],v,d,c};head[u]=cnt_e;flow[cnt_e]=0;
}
inline void link(int u,int v,int d,int c)
{
add_edge(u,v,d,c),add_edge(v,u,0,-c);
}
inline void link(int u,int v,int l,int r,int c)
{
link(u,v,r-l,c);ind[v]+=l,oud[u]+=l;
}
deque<int>q;
int spfa()
{
R(i,1,T) now[i]=head[i],dis[i]=inf;
q.pb(S);
dis[S]=0;
int u,v;
while((int)q.size()>0)
{
u=q.front();q.pop_front();
vis[u]=0;
for(int i=head[u];i;i=e[i].nxt)
{
v=e[i].to;
if(dis[v]>dis[u]+e[i].cst&&e[i].cap)
{
dis[v]=dis[u]+e[i].cst;
if(!vis[v]) vis[v]=1,q.pb(v);
}
}
}
return dis[T]<inf;
}
int dfs(int u,int mc)
{
if(u==T) return mc;
vis[u]=1;
int ret=0,v,k;ret=0;
for(int &i=now[u];i&&ret<mc;i=e[i].nxt)
{
v=e[i].to;
if(e[i].cap&&dis[v]==dis[u]+e[i].cst&&!vis[v])
{
k=dfs(v,min(mc-ret,e[i].cap));
e[i].cap-=k,e[i^1].cap+=k;
ret+=k;
if(ret==mc) break;
}
}
vis[u]=0;
return ret;
}
int dinic()
{
int ret=0,ans=0;
int tmp;
while(spfa())
{
tmp=dfs(S,inf);
ret+=tmp;
ans+=dis[T]*tmp;
}
return ret==sumf?ans:-1;
}
signed main()
{
n1=read(),n2=read(),m=read(),cstr=read(),cstb=read();
s=n1+n2+1,t=s+1,S=t+1,T=S+1;
scanf("%s",str+1);
R(i,1,n1)
{
if(str[i]=='R') link(s,i,1,inf,0);
else if(str[i]=='B') link(i,t,1,inf,0);
else link(s,i,0,inf,0),link(i,t,0,inf,0);
}
scanf("%s",str+1);
R(i,1,n2)
{
if(str[i]=='R') link(i+n1,t,1,inf,0);
else if(str[i]=='B') link(s,i+n1,1,inf,0);
else link(s,i+n1,0,inf,0),link(i+n1,t,0,inf,0);
}
int u,v;
R(i,1,m) u=read(),v=read(),link(u,v+n1,0,1,cstr),idr[i]=cnt_e,link(v+n1,u,0,1,cstb),idb[i]=cnt_e;
R(i,1,t)
{
if(ind[i]>oud[i]) link(S,i,ind[i]-oud[i],0);
if(ind[i]<oud[i]) link(i,T,oud[i]-ind[i],0);
sumf+=abs(ind[i]-oud[i]);
}
link(t,s,inf,0);
sumf>>=1;
int tmp=dinic();
writeln(tmp);
if(~tmp)
{
R(i,1,m)
{
if(e[idr[i]].cap) printf("R");
else if(e[idb[i]].cap) printf("B");
else printf("U");
}
}
}
CF1097E
给定一个长度为\(n\)的排列,设\(f(n)\)表示把任意一个长度为\(n\)的排列划分成最少的上升和下降子序列的个数的最大值,现在你要把这个排列划分成不超过\(f(n)\)个上升或下降子序列。
\(n\leq 10^5\)
首先考虑\(f\)是多少。事实上\(f(n)+1\)是最少的\(x\)满足\(1+\ldots +x>n\)。
考虑排列\(1,3,2,6,5,4,10,9,8,7,\cdots,\)显然可以卡到这个上界。
设当前排列的\(\texttt{LIS}\)长度为\(l\),若\(l>f(n)\),那么显然可以直接把它划分出来;
若\(l\leq f(n)\),那么由于最长反链等于最小链覆盖,我们找到一个最小链覆盖即可。
事实上在二分\(dp\)做法求\(\texttt{LIS}\)的过程中,\(dp\)数组每一位上就对应了一个\(LDS\)。因此\(dp\)的时候就能直接求出\(\texttt{LDS}\)划分了。
int n,k;
int a[111111],vis[111111];
int dp[111111],pre[111111],q[111111];
int cnt;
vector<int>ans[111111];
void solve(int k)
{
int mxlis=0;q[0]=0;
R(i,1,n) if(!vis[a[i]])
{
int l=1,r=mxlis,ans=0;
while(l<=r)
{
int mid=(l+r)>>1;
if(a[q[mid]]<a[i]) ans=mid,l=mid+1;
else r=mid-1;
}
dp[i]=ans+1;
pre[i]=q[ans];q[ans+1]=i;
ckmax(mxlis,ans+1);
}
if(mxlis>=k)
{
++cnt;
for(int i=q[mxlis];i;i=pre[i]) ans[cnt].pb(a[i]),vis[a[i]]=1;
reverse(ans[cnt].begin(),ans[cnt].end());
solve(k-1);
}
else
{
R(i,1,n) if(!vis[a[i]]) ans[cnt+dp[i]].pb(a[i]);
cnt+=mxlis;
}
}
signed main()
{
for(int _=read();_--;)
{
cnt=k=0;R(i,0,n+5) vis[i]=0;
n=read();
R(i,1,n) a[i]=read();
for(;k*(k+1)<=n+n;k++);
solve(k);
writeln(cnt);
R(i,1,cnt)
{
writesp((int)ans[i].size());
for(int x:ans[i]) writesp(x);puts("");
ans[i].clear();
}
}
}
CF1261E
一个数列\(a_1,\cdots ,a_n\),所有数字都是正整数。你每次操作可以选定一个集合\(S\),把\(S\)中的数字减\(1\),至多操作\(n+1\)次把所有所有数字变成\(0\)。并且要求任意两次操作的集合都互不相同。
给出一组方案。
\(n\leq 1000,1\leq a_i\leq n\)
把问题稍微转化一下,变成一个\(n+1\)行\(n\)列的零一矩阵,每一列的和有限制,并且任意两行互不相同。
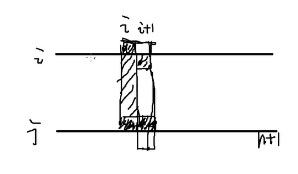
考虑如果数列中全是\(n\)怎么办,显然可以挖掉零一矩阵的一个对角线,然后多填一行\(1\)。(事实上可以多画几个例子找找感觉)
这给我们了启发,事实上我们可以把所有数字从小到大排序,对于第\(i\)列,我们从第\(i\)行开始填(填到底部就再从顶部开始填)
怎样证明这样任意两行都不相同呢?不妨设两行分别为\(i,j(i<j)\),如果要想等的话必须要\((j,i)=1\),但由于我们从小到大排序,因此\((j,i)=1\)就必然有\((j,i+1)=1\),于是为了保证相等自然也有\((i,i+1)=1\),但我们的填法保证了\((i,i+1)=0\)。
因此任意两行都互不相同,这是一个合法的构造。
const int N=1111;
int n;
pii a[N];
char s[N][N];
signed main()
{
n=read();
R(i,1,n) a[i]=mkp(read(),i);
sort(a+1,a+n+1);
R(i,1,n) R(j,0,n) s[(i+n-j)%(n+1)][a[i].se-1]='0'+(j<a[i].fi);
writeln(n+1);R(i,0,n) printf("%s\n",s[i]);
}
AGC004F
给你一棵全白的树或环套树。
你每次可以选择连接一条连接两个同色点的边,将两个端点反色。
问变成全黑的最小步数,或判断无解。
\(n\leq 10^5\)
先考虑树怎么做。
我们把奇数深度的点视为一个坑,偶数深度的点上面有一个球,每次操作相当于把球扔进坑里(白变黑)或者把某个坑里的球扒出来(黑变白)。最后要求所有球都在坑里(全黑)。
考虑一下一个球经过若干个有球的坑(或者没球的偶数深度点)落在某个空的坑里对应的操作是什么,事实上这就相当于把后面一个坑里的球扒出来,然后把前面的球塞进去,把后面的球当作前面的球继续操作。
不难发现这样的代价正是走过的路径长度,因此问题变成了:每个球匹配一个坑,求最小的匹配代价和。
显然,把坑视为\(-1\),球视为\(1\),答案就是\(\sum |\)每个子树权值和\(|\)。这是因为每棵子树需要把那些不均衡的点通过它的父亲边运出来。特别的,如果球和坑的数量不同显然无解。
(事实上更形式化的,问题就是每次可以把\(u+=1,v-=1\),代价为\(dist(u,v)\),为最小的代价把所有权值变成\(0\))
如果是环套树,讨论一下环的奇偶性。
若环为奇环:
断开环上的任意一条边\(u,v\)使它变成树,考虑到\(u,v\)的深度奇偶性必然相同(即同时是球或同时是坑),我们可以额外操作\(u,v\)这条边使得球的个数\(+2\)或\(-2\)。
于是此时有解当且仅当球的个数和坑的个数奇偶性相同。于是变成树了之后,可能会缺少若干个球或者若干个坑,那么就假设\(u,v\)上有多个球或者坑即可(多的数量可以直接计算出来)。
若环为偶环:
仍然考虑断开\(u,b\),但这次\(u,v\)深度的奇偶性不同,考虑操作一次\(u,v\)仍然相当于把球扔进洞或者把球从洞里扒出来,因此有解仍然当且仅当坑和球的数量相同。
但是这个时候有可能会因为新加的这条边让操作数量变小,不妨设这条边操作了\(x\)次(即假设\(u\)的权值加上了\(x\),\(v\)的权值减掉了\(x\),可以操作负数次),那么总操作次数是\(|x|+\sum|\)子树权值和\(|\)。
只不过这里的子树权值和是和\(x\)有关的一次函数,现在要求一个\(x\)使得上式最小,这是个经典问题,取中位数即可。
int dep[222222];
vector<int>e[222222],vec;
int dp[222222],tag[222222];
int n,m,cnt;
int cir_len,cir_L,cir_R;
int ans;
void dfs1(int u,int f)
{
dp[u]=(dep[u]&1)?1:-1;
cnt+=dp[u];
for(int v:e[u]) if(v^f)
{
if(dep[v]) cir_len=abs(dep[u]-dep[v])+1,cir_L=u,cir_R=v;
else dep[v]=dep[u]+1,dfs1(v,u);
}
}
void dfs2(int u,int f)
{
for(int v:e[u]) if(v^f)
{
if((u==cir_L&&v==cir_R)||(u==cir_R&&v==cir_L)) continue;
dfs2(v,u);
tag[u]+=tag[v];
dp[u]+=dp[v];
}
if(!tag[u]) ans+=abs(dp[u]);
else vec.pb(dp[u]*tag[u]);
}
signed main()
{
n=read(),m=read();
int u,v;R(i,1,m) u=read(),v=read(),e[u].pb(v),e[v].pb(u);
dep[1]=1;
dfs1(1,0);
if(m==n-1)
{
if(cnt) return puts("-1")&0;
}
else if(cir_len%2)
{
if(cnt%2) return puts("-1")&0;
int t=cnt/2;
ans+=abs(t),dp[cir_L]-=t,dp[cir_R]-=t;
}
else
{
if(cnt) return puts("-1")&0;
tag[cir_L]=1,tag[cir_R]=-1;
}
dfs2(1,0);
vec.pb(0);
sort(vec.begin(),vec.end());
int tmp=vec[(int)vec.size()>>1];
R(i,0,(int)vec.size()-1) ans+=abs(tmp-vec[i]);
writeln(ans);
}
AGC006E
一个\(n\times 3\)的网格,每次你可以选定一个九宫格并做中心对称。
给定一个指定状态,问从\((i,j)\)为\(i+3j-3\)的网格是否能到达给定状态。
\(n\leq 10^5\)
先分析一下这个操作下的不变量是什么。
首先一列里面三个数字要么是顺着的要么是反着的,它们不可能被分开。并且一次交换只能交换奇数位/偶数位中的相邻两个。
按奇偶位置分开,设\(f(1/0)\)表示奇数位/偶数位上反转列数量的奇偶性,\(g(1/0)\)表示奇数位/偶数位的逆序对数量的奇偶性。
首先一次奇数位为中心的操作会让\(g(0)\oplus =1,f(1)\oplus =1\),偶数位的操作相反。因此总有\(f(0)=g(1),f(1)=g(0)\)。
接下来考虑证明这是充分条件。
我们先把所有列不管正反先交换到对应位置。然后设小写字母表示原来的列,大写字母表示反转之后的列:

上述构造证明了任意距离为\(2\)的两列都可以直接被反转。
由于奇偶性的保证,刚交换完时的\(f\)必然和最终的\(f\)相等,因此直接反转必然可以成为答案。
事实上如果\(n\leq 1000\),可以输出方案,步数级别\(O(n^2)\)。
不要求输出方案只需要求逆序对数量,直接bit即可(或者由于只需要求奇偶性可以做到线性)。
此时问题被转化成一个\(01\)序列每次可以同时翻转相邻两位,最后使序列变成全\(0\)序列。当\(1\)的个数为偶数就有解。
具体怎么构造:
先用偶数位交换相邻奇数位,将奇数位弄到对应的位置上,此时不用考虑奇数位列上的数是正还是反。这样操作次数为\(g(1)\)(奇数位逆序对个数),这个时候每交换一次两个相邻奇数位,所以此时偶数位上也会恰好有\(g(1)\)个反转的列。
但是目标有\(f(0)\)个反转的位,所以\(f(0)\)和\(g(1)\)的奇偶性应相同,然后就可以用上面说的那个做。
总结一下就是先用偶数将奇数操作到对应位置上,用奇数将偶数操作到对应位置上,然后可以发现偶数位操作完之后恰好有\(g(1)\)反着的位,然后目标是\(f(0)\)个反着的位,这两个东西奇偶性相同,就可以每次反转相邻两个,反转到目标位置。
int n;
int a[111111][4];
int f[2],g[2];
inline int lowbit(int x){return x&-x;}
struct BiT
{
int v[111111];
inline void modify_add(int x,int k=1){for(int i=x;i<=n;i+=lowbit(i))v[i]^=k;}
inline int query(int x){int ret=0;for(int i=x;i;i-=lowbit(i))ret^=v[i];return ret;}
}b[2];
signed main()
{
n=read();
R(j,1,3) R(i,1,n) a[i][j]=read()+2;
R(i,1,n)
{
if(a[i][1]/3!=a[i][2]/3||a[i][2]/3!=a[i][3]/3||((a[i][1]/3-i)%2)||(a[i][2]%3!=1)) return puts("No")&0;
}
R(i,1,n)
{
f[i&1]^=(a[i][1]%3>0);
int t=n-a[i][1]/3+1;
g[i&1]^=b[i&1].query(t);
b[i&1].modify_add(t);
}
if(f[0]^g[1]||f[1]^g[0]) puts("No");
else puts("Yes");
}
AGC018F
给定两棵带标号的有根树,你需要给每个点赋权值,使得每棵子树内部的权值和为\(1\)或\(-1\)。给出方案或报告无解。
\(n\leq 10^5\)
首先可以算出每个点最终权值的奇偶性,如果两棵树中的对应点奇偶性不同,显然无解。
事实上只要有解,就可以给出一个权值都是\(-1,0,1\)的方案。
首先如果一个点要是偶数(即有奇数个儿子),那么可以直接将它的权值设为\(0\)。
否则,它的子树内(不含它自己)必然有偶数个权值为奇数的点。我们把这些点两两配对,使得每个权值为奇数的点的子树中,不存在孤立的权值为奇数的点(即全部两两配对完毕)。
这是很好构造的,dfs先匹配完子树,然后剩余点两两匹配即可。
只要能够对于匹配点,一个点取\(1\),另一个取\(-1\),就可以满足要求了。
我们把一对匹配点连边,把两棵树对应的图合起来,容易发现这是个二分图(因为不会有相邻的两条边来自于同一棵树)。
因此直接黑白染色,黑点填\(1\),白点填\(-1\)即可。
复杂度\(O(n)\)。
int n,siz[222222];
namespace tdg
{
int vis[222222],col[222222];
vector<int>e[222222];
void dfs(int u,int f=0)
{
vis[u]=1;col[u]=col[f]^1;
for(int v:e[u]) if(!vis[v]) dfs(v,u);
}
void solve()
{
puts("POSSIBLE");
R(i,1,n) if(!vis[i]) dfs(i);
R(i,1,n) if(siz[i]%2==0) printf(col[i]?"1 ":"-1 ");else printf("0 ");
}
}
namespace tr1
{
int rt;
vector<int>e[222222],stk;
inline void init()
{
int f;
R(i,1,n)
{
f=read();
if(~f) e[f].pb(i);
else rt=i;
}
}
void dfs(int u=rt,int l_s=0)
{
for(int v:e[u]) dfs(v,(int)stk.size());
while((int)stk.size()-2>=l_s)
{
static int x,y;
x=stk.back(),stk.pop_back(),y=stk.back(),stk.pop_back();
tdg::e[x].pb(y),tdg::e[y].pb(x);
}//兄弟之间需要确定的点两两匹配
if((int)e[u].size()%2==0) stk.pb(u);
}
}
namespace tr2
{
int rt;
vector<int>e[222222],stk;
inline void init()
{
int f;
R(i,1,n)
{
f=read();
if(~f) e[f].pb(i);
else rt=i;
}
}
void dfs(int u=rt,int l_s=0)
{
for(int v:e[u]) dfs(v,(int)stk.size());
while((int)stk.size()-2>=l_s)
{
static int x,y;
x=stk.back(),stk.pop_back(),y=stk.back(),stk.pop_back();
tdg::e[x].pb(y),tdg::e[y].pb(x);
}
if((int)e[u].size()%2==0) stk.pb(u);
}
}
inline void check()
{
R(i,1,n)
{
if(tr1::e[i].size()%2!=tr2::e[i].size()%2) puts("IMPOSSIBLE"),exit(0);
}
R(i,1,n) siz[i]=(int)tr1::e[i].size();
}
signed main()
{
n=read();
tr1::init();
tr2::init();
check();
tr1::dfs();
tr2::dfs();
tdg::solve();
}
AGC027D
构造一个\(n\times n\)的矩阵,每个元素是\([1,10^{15}]\)中的整数且互不相同,你还需要确定一个正整数\(m\),使得矩阵中任意相邻的两个元素\(x,y\)都有\(\max (x,y)\bmod \min(x,y)=m\)。
\(n\leq 500\)
令\(m=1\),考虑给棋盘黑白染色后,白点都是较小值,黑点都是较大值。然后令黑点为周围四个白点的\(\texttt{LCM}+1\)。
考虑每个主对角线和副对角线都分别赋一个互不相同的质数,令每个白点的值为其所在主对角线和副对角线对应质数的乘积。
因此大概需要处理前\(2000\)个质数,最终最大值大概是\(4\times 10^{14}\),可以通过。
const int N=555;
int ans[N][N];
int n;
int pri[22222],cnt_pr,vis[22222];
inline int gcd(int a,int b) {return !b?a:gcd(b,a%b);}
inline int lcm(int a,int b) {return a/gcd(a,b)*b;}
void eushai()
{
R(i,2,20000) {
if(!vis[i]) pri[++cnt_pr]=i;
for(int j=1;pri[j]*i<=20000&&j<=cnt_pr;j++) {
vis[pri[j]*i]=1;
if(i%pri[j]==0) break;
}
}
}
signed main()
{
n=read();
if(n==2) return puts("4 7\n23 10")&0;
eushai();
R(i,0,n+1) ans[0][i]=ans[i][0]=ans[n+1][i]=ans[i][n+1]=1;
R(i,1,n) R(j,1,n) if(!((i+j)%2)) ans[i][j]=pri[(i+j)/2]*pri[(i-j)/2+n+n];
R(i,1,n)
{
R(j,1,n)
{
if((i+j)%2)
{
ans[i][j]=1;
ans[i][j]=lcm(ans[i][j],ans[i-1][j]);
ans[i][j]=lcm(ans[i][j],ans[i+1][j]);
ans[i][j]=lcm(ans[i][j],ans[i][j+1]);
ans[i][j]=lcm(ans[i][j],ans[i][j-1]);
ans[i][j]++;
}
}
}
R(i,1,n) {
R(j,1,n) printf("%lld ",ans[i][j]);puts("");
}
}
AGC027F
给定两棵树\(A,B\),你每次可以把\(A\)的某个叶节点接到其他节点上。每个节点最多只能被操作一次。
问\(A\)能否操作到\(B\),如果能输出最小操作次数。
\(n\leq 50\)
如果\(A\)到\(B\)存在某个节点没有被操作过(设为\(r\)),那么两棵树都以\(r\)为根,不难发现一定是从有根树的叶节点开始做起操作。
并且由于一个点最多被操作一次,因此一个点被操作当且仅当他在两棵树中的父亲不同。且它的操作时间必然在\(A\)中它的父亲操作之前,\(B\)中的父亲操作之后。
因此连边拓扑排序即可,不难发现只要能拓扑排序出来,必然就是一个合法解。
如果不存在节点没有操作过,可以直接暴力枚举第一次操作的叶子以及它操作之后的父亲,这样在之后它就是个不动点(不能被第二次操作了),提根做上述拓扑排序即可。
总复杂度\(O(n^3)\)。
int n;
vector<int>a[66],b[66],e[66];
int mp[66][66],vis[66];
int ans;
int cnt;
void dfs1(int u,int f)
{
vis[u]=1;++cnt;
for(int v:a[u]) if(v^f&&mp[u][v]) dfs1(v,u);
}
void dfs2(int u,int f)
{
for(int v:a[u]) if(v^f)
{
dfs2(v,u);
if(!vis[u]) e[v].pb(u);
}
}
void dfs3(int u,int f)
{
for(int v:b[u]) if(v^f)
{
dfs3(v,u);
if(!vis[u]) e[u].pb(v);
}
}
int in[66];
int topo()
{
R(u,1,n) for(int v:e[u]) in[v]++;
static int tot;tot=0;
deque<int>q;
R(i,1,n) if(!in[i]) q.pb(i),++tot;
while((int)q.size()>0)
{
int u=q.front();q.pop_front();
for(int v:e[u])
{
--in[v];
if(!in[v]) q.pb(v),++tot;
}
}
return (tot==n);
}
signed main()
{
for(int _=read();_;_--)
{
n=read();
R(i,1,n)
{
a[i].clear(),b[i].clear();
R(j,1,n) mp[i][j]=0;
}
int u,v;
R(i,2,n) u=read(),v=read(),a[u].pb(v),a[v].pb(u);
R(i,2,n) u=read(),v=read(),b[u].pb(v),b[v].pb(u),mp[u][v]=mp[v][u]=1;
ans=n+1;
R(i,1,n)
{
cnt=0;
R(j,1,n) vis[j]=0;
dfs1(i,0);
R(j,1,n) e[j].clear(),in[j]=0;
dfs2(i,0),dfs3(i,0);
if(topo()) ckmin(ans,n-cnt);
}
R(i,1,n) if((int)a[i].size()==1)
{
R(j,1,n)
{
R(k,1,n) e[k].clear(),in[k]=0,vis[k]=0;
dfs2(j,0),dfs3(i,0);
if(topo()) ckmin(ans,n);
}
}
if(ans==n+1) puts("-1");
else printf("%lld\n",ans);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号