汽车质心绝对加速度数学推导和滑模控制实例

1. 线性二自由度汽车质心绝对加速度在车辆坐标系下的公式

在汽车线性二自由度微分方程那篇博客中，我具体推导了$a_y$，但是用了近似和忽略。下面将用向量的方法，详细推导出$a_x、a_y$。

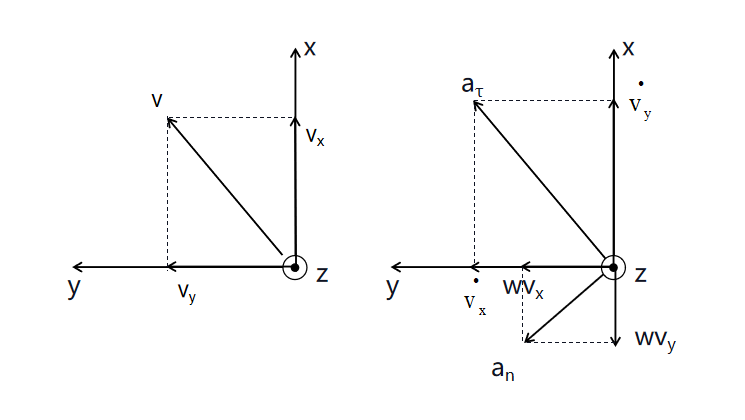
下面是推导的过程：

$$\begin{aligned} a&=a_\tau+a_n\\ &=\overset{·}{v_x}\overset{\rarr}{x}+\overset{·}{v_y}\overset{\rarr}{y}+w\overset{\rarr}{z}\times(v_x\overset{\rarr}{x}+v_y\overset{\rarr}{y})\\ &=\overset{·}{v_x}\overset{\rarr}{x}+\overset{·}{v_y}\overset{\rarr}{y}+wv_x\overset{\rarr}{z}\times\overset{\rarr}{x}+wv_y\overset{\rarr}{z}\times\overset{\rarr}{y}\\ &=\overset{·}{v_x}\overset{\rarr}{x}+\overset{·}{v_y}\overset{\rarr}{y}+wv_x\overset{\rarr}{y}-wv_y\overset{\rarr}{x}\\ &=(\overset{·}{v_x}-wv_y)\overset{\rarr}{x}+(\overset{·}{v_y}+wv_x)\overset{\rarr}{y}\\ &=a_x \overset{\rarr}{x}+a_y \overset{\rarr}{y} \end{aligned}$$

其中$\tau$向就是切向，而$n$向就是法向。

2. 一个汽车跟踪问题的滑模控制实例

例：汽车队列跟踪问题可以抽象出如下的模型：$\overset{··}{x}=-\overset{·}{x}\ ^2+u$, 设计控制律$u$，使$x\rarr x_d\quad (t\rarr \infty)$

解：设$\epsilon=x-x_d$，则$\overset{·}{\epsilon}=\overset{·}{x}-\overset{·}{x_d}$，$\overset{··}{\epsilon}=\overset{··}{x}-\overset{··}{x_d}$

可以设计切换函数$S(\epsilon)=k\epsilon+\overset{·}{\epsilon}\quad (k>0)$

接下来可以证明切换函数的滑模稳定性、存在性、可达性。

2.1 滑模稳定性

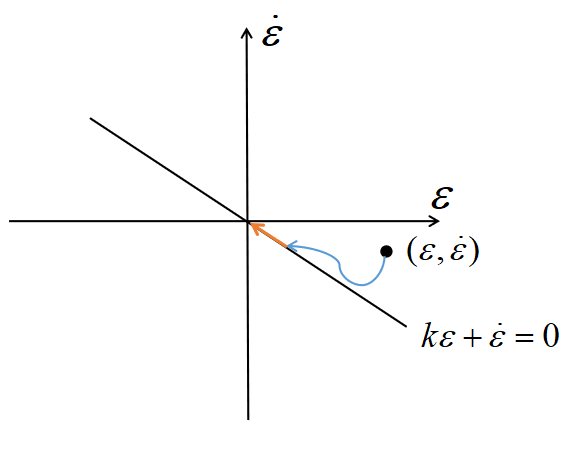
滑模稳定性是指$S\rarr0$时，$\epsilon\rarr0$且$\overset{·}{\epsilon}\rarr0$，即点$(\epsilon,\overset{·}{\epsilon})$会沿着滑模面$k\epsilon+\overset{·}{\epsilon}=0$到达原点。如下图中的黄线所示。

可以很快证明滑模稳定性，根据$k\epsilon+\overset{·}{\epsilon}=0$，可以解得$\epsilon=ce^{-kt}$，$\overset{·}{\epsilon}=-cke^{-kt}$

当$t\rarr \infty$时，可知$\epsilon\rarr0$，$\overset{·}{\epsilon}\rarr0$，滑模存在稳定性。

2.2 滑模存在性与可达性

滑模控制系统存在性的充分条件是 $\underset{S\rarr0}{lim}S\overset{·}{S}<0$，该条件可以保证系统在滑模面附近的任意初始状态，都能到达滑模面，是局部到达的条件。

滑模控制系统可达性的充分条件是 $S\overset{·}{S}<0$，该条件可以保证系统在状态空间的任意位置，都能到达滑模面，是全局可达条件。

上面两个要素都是指如何到达滑模面的事情，如上图的蓝线所示。

接下来证明滑模可达性（也就证明了存在性）。

可以采用等速趋近律$\overset{·}{S}=-\lambda sgn(s)\quad(\lambda>0)$，在该趋近律下，$S\overset{·}{S}<0$成立。因为$S>0$时，$\overset{·}{S}<0$；$S<0$时，$\overset{·}{S}>0$。

将切换函数$S(\epsilon)=k\epsilon+\overset{·}{\epsilon}$左右两边求导，得到

$$\overset{·}{S}=k\overset{·}{\epsilon}+\overset{··}{\epsilon}$$

再将$\overset{··}{\epsilon}=\overset{··}{x}-\overset{··}{x_d}$带入上式，得到

$$\overset{·}{S}=k\overset{·}{\epsilon}+\overset{··}{x}-\overset{··}{x_d}$$

得到的$\overset{··}{x}$与控制律$u$存在关系$\overset{··}{x}=-\overset{·}{x}\ ^2+u$，所以将它代入上式就引入了控制律。

$$\overset{·}{S}=k\overset{·}{\epsilon}-\overset{··}{x_d}-\overset{·}{x}\ ^2+u$$

将上式与等速趋近律联立消去$\overset{·}{S}$，得到

$$u=-\lambda sgn(s)-k\overset{·}{\epsilon}+\overset{··}{x_d}+\overset{·}{x}\ ^2$$

$u$可以看成$u_{equ}$和$u_N$两部分：

• 等效控制部分 $u_{equ}=-k\overset{·}{\epsilon}+\overset{··}{x_d}+\overset{·}{x}\ ^2$

• 反馈控制部分 $u_N=-\lambda sgn(s)$