【DeepLearning】基本概念:卷积、池化、Backpropagation
终于有了2个月的空闲时间,给自己消化沉淀,希望别有太多的杂事打扰。在很多课程中,我都学过卷积、池化、dropout等基本内容,但目前在脑海中还都是零散的概念,缺乏整体性框架,本系列博客就希望进行一定的归纳和梳理,谋求一个更清晰的思路。
## Outline
## Notes
【卷积(Convolution)】
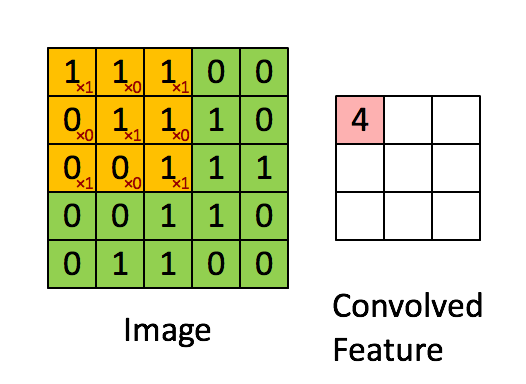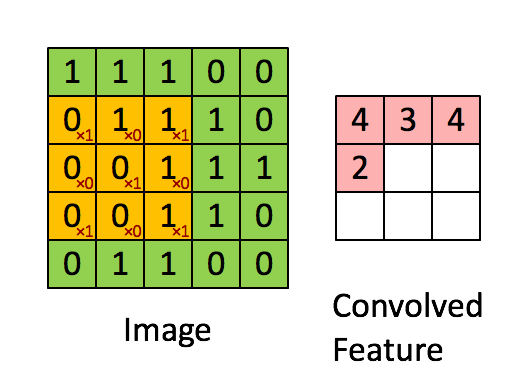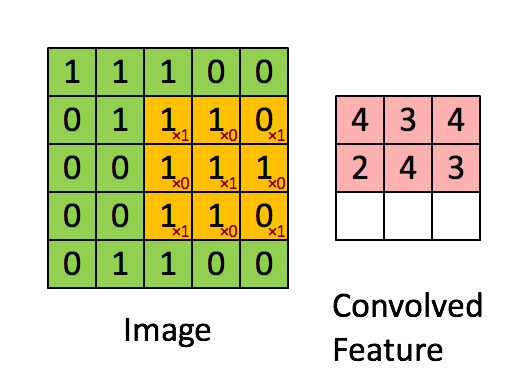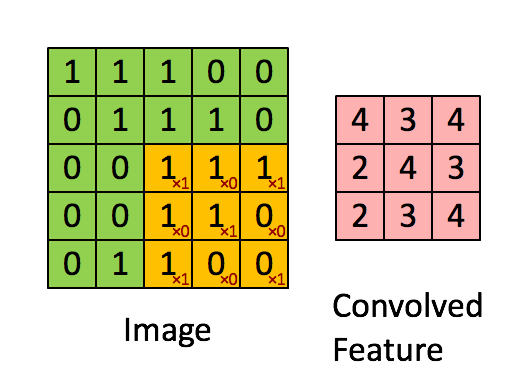
卷积的目的就是从原始数据中提取出特征,过程是利用卷积核(kernel)按照下面动图的规则进行计算(做点乘),得到的结果称为卷积特征(Convolved Feature)。其中卷积核又叫过滤器(Filter),他是一个W核矩阵,而W矩阵中各个元素的值正是我们进行模型训练时要训练的参数。即CNN的一个主要任务就是学习出卷积核。
很有趣的是,一个卷积核往往只对图中的某一特征感兴趣(如边缘信息、斜线、特定颜色等等),下图就展示了经过不同的kernel处理后得到的特征图。而在我们实际分析时,往往要综合很多内容,这就需要多个卷积核同时工作,如下图动图所示,就是在处理实际问题时的一个例子。


值得注意的是,我们在上述分析时使用的都是黑白图像,其对应的卷积核都是二维的。而对于彩色图像,这个图像的数据往往是一个三维的数组(每个像素对应有RGB三个颜色通道),这个时候对应的卷积核就也是三维的了,对于更高维的数据,卷积核的维度也相应地改变。下图来自cs231n课程,展示的就是这样的过程:

我们可以看到,在这个例子中:
- Input size:输入图片的大小为 5*5*3
- Filter size:使用了W0、W1两个filter,大小均为3*3*3
- Stride:卷积时的步长为2
- padding:填充大小为1
根据上述的公式,我们可以计算出特征图的大小为3.
值得注意的是:
- 左边数据在变化,每次滤波器都是针对某一局部的数据窗口进行卷积,这就是所谓的CNN中的局部感知机制。
- 数据窗口滑动,导致输入在变化,但中间滤波器Filter w0的权重(即每个神经元连接数据窗口的权重)是固定不变的,这个权重不变即所谓的CNN中的权重共享机制。
【tensorflow-conv】
tf.nn.conv2d(input,filter, strides, padding, data_format=’NHWC’)
- input: 4-D 的Tensor, 每个dimension的意思由data_format指定,默认是[batch, Height, Width, Channel]。
- batchsize 表示样本数量。
- Height/Width是图片的高度/宽度
- Channel是深度,即决定了图片是灰度图还是彩色图。若是灰度图则为1,若是彩色图则为3。
- filter: 这个filter也是一个4-D的Tensor,每个dimension分别表示 [filter_height, filter_width, in_channels, out_channels]。
- 通常地称[filter_height, filter_width, in_channels]为单个filter的size,而且filter_height, filter_width一般为奇数并且相等。
- in_channel必须跟input参数中的Channel相等,卷积运算时,从input中取一个大小为[filter_height, filter_width, in_channels]的slice window跟 单个filter做卷积运算。
- out_channels表示有多少个这样的filter。因为filter一般用于特征的抽取,所以out_channels决定了卷积层最终输出的channel(depth)。
- strides: 4-D的Tensor, 表示在对input做卷积运算时,在每个dimension上的步长。
- 跟input参数一样,每个dimension的顺序由data_format决定。
- 通常地在Height, Width上步长为1或者2,而batch, Channel的步长设置为1。
- padding: “SAME” 或者 “Valid”。
- Same表示边缘自动补零,卷积层的输出的height/width 跟input层的height/width相同。
- Valid表示no padding,不自动填充,输出层的公式为 (height−filter_heigth)/stride_height+1 (width也是一样)。
weights = {
'wc1': tf.Variable(tf.random_normal([3,3,1,64],stddev = 0.1))
}
_input = tf.reshape(input,shape = [-1,28,28,1])
_conv1 = tf.nn.con2v(_input , w['wc1'],strides = [1,1,1,1],padding='Same')
【池化(Pooling)】
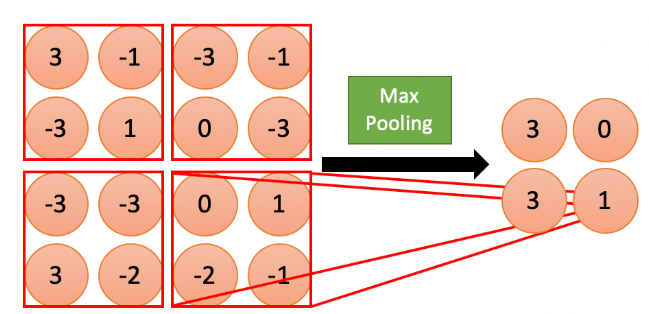
池化操作(pooling)的本质就是采样,可以采取的操作有:最大化、平均化、加和等。最常用并且被证明效果很好的池化操作为最大池化。
所谓最大池化就是,我们定义一个空间临域(比如一个2X2的窗口),并从窗口内的特征图中取出最大的元素。
池化的意义如下:
- 有效地减少参数但又能保留主要特征
- 有效的防止过拟合(使得卷积核偏好的特征得到保留和增强,削弱其他干扰)
- 发挥特征图的“不变性”(invariance),特征的平移、旋转、尺寸变化对网络的影响可以得到一定程度上的缓解
tf.nn.max_pool(value, ksize = [1,f,f,1], strides = [1,s,s,1], padding = ‘SAME’, data_format=’NHWC’)
- value: 4-D的tensor, 一般地就是上面conv2d的输出,所以输入通常是feature map,依然是
[batch, height, width, channels]这样的shape; - ksize: 定义了池化窗口的大小,取一个四维向量,一般是
[1, height, width, 1],因为我们不想在batch和channels上做池化,所以这两个维度设为了1; - strides:和卷积类似,窗口在每一个维度上滑动的步长,一般也是
[1, stride,stride, 1] - padding:和卷积类似,可以取'VALID' 或者'SAME'
input = tf.reshape(input,[1,4,4,2]) pooling=tf.nn.max_pool(input,[1,2,2,1],[1,2,2,1],padding='VALID')
反向传播是在求解损失函数L对参数w求导时候用到的方法,目的是通过链式法则对参数进行一层一层的求导,进而实现对 W 的更新。
有一个博客很好的总结了相关的内容:https://blog.csdn.net/u014688145/article/details/78691262
- (基本概念)靠近输入的神经元会比靠近输出的神经元的梯度成指数级衰减。总的来说,就是在这个深度网络中,梯度相当不稳定(unstable)。
-
靠近输出层的hidden layer 梯度大,参数更新快,所以很快就会收敛;而靠近输入层的hidden layer 梯度小,参数更新慢,几乎就和初始状态一样,随机分布。这种现象就是梯度弥散(vanishing gradient problem)。
-
而在另一种情况中,前面layer的梯度通过训练变大,而后面layer的梯度指数级增大,这种现象又叫做梯度爆炸(exploding gradient problem)。
-
- (问题一)sigmoid时,消失和爆炸哪个更易发生?
- 最普遍发生的是梯度消失问题。
- 量化分析梯度爆炸出现时a的输出范围:因为sigmoid导数最大为1/4,故只有当abs(w)>4时才可能出现。由此计算出a的数值变化范围很小,仅仅在此窄范围内会出现梯度爆炸问题。
- (问题二)如何解决梯度消失和梯度爆炸?
- 梯度消失:使用ReLU,maxout等替代sigmoid。
- 梯度爆炸:使用Gradient Clipping(梯度裁剪)。通过Gradient Clipping,将梯度约束在一个范围内,这样不会使得梯度过大。
- (问题三)为何用Relu好使?即Relu和sigmoid区别:
- sigmoid函数值在[0,1],ReLU函数值在[0,+无穷],所以sigmoid函数可以描述概率,ReLU适合用来描述实数;
- sigmoid函数的梯度随着x的增大或减小和消失,而ReLU不会。

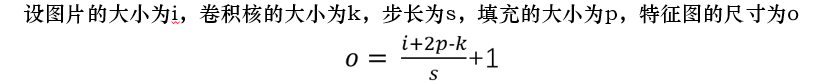

 浙公网安备 33010602011771号
浙公网安备 33010602011771号