【每日算法】位运算之N皇后问题

位运算技巧

x&(-x) 获取二进制位中最后一个1的位置
x&(x-1) 把二进制位中的最低位的1置成0

题目

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

普通解法

class Solution(object):
    def solveNQueens(self, n):
        res=[]#定义返回的结果
        def helper(row,hang,pie,na,path):
            if row==n:#如果遍历到最后一行了，则把结果保存起来
                res.append(path)
                return
            #开始进行一行的逐个尝试放置皇后
            for j in range(n):
                #如果一个位置的同列，右斜 左斜已经有元素了，则此位置不能放置皇后
                if j in hang or row-j in pie or row+j in na:
                    continue
                #找到一个放置皇后的位置后，计算出棋盘的布局
                tmp="."*j+"Q"+"."*(n-1-j)
                #一行确定一个皇后位置后，开始进行下一行的查找，并把当前的位置信息分别保存集合里
                helper(row+1,hang|{j},pie|{row-j},na|{row+j},path+[tmp])
        #从第0行开始往下找
        helper(0,set(),set(),set(),[])
        return res

位运算的解法

可以利用位运算记录皇后的信息，n*n的棋盘，则用n位的二进制位表示，位运算从右向左依次低位到到位，为了对应我们遍历棋盘从右向左遍历。

有上面的解法可知，我们需要三个变量来保存曾经的皇后信息，columns记录每列的上的皇后信息、diagonals1记录左斜线上的皇后信息、diagonals2记录右斜线上的皇后信息，以8行

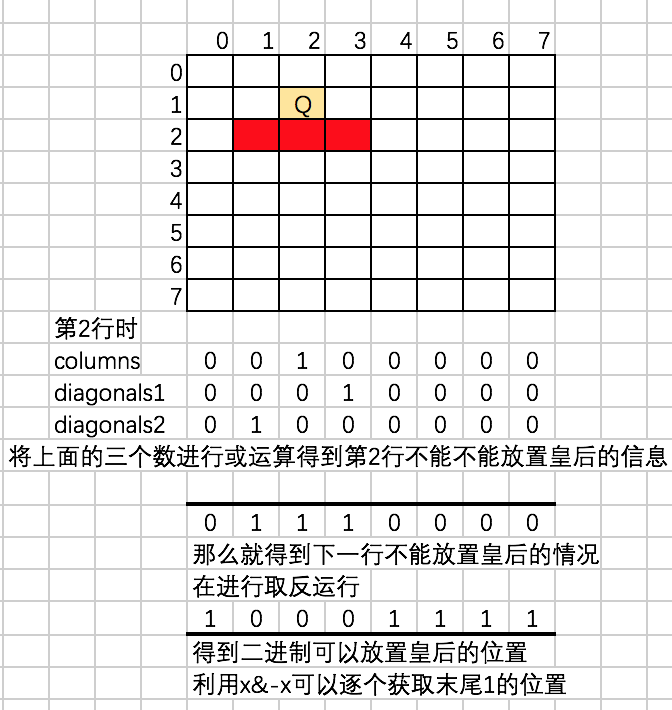
代码如下

class Solution:
    def solveNQueens(self, n):
        res=[]#定义返回的结果
        def helper(row,columns,diagonals1,diagonals2,path):
            if row==n:#如果遍历到最后一行了，则把结果保存起来
                res.append(path)
                return
            #获取有效的皇位的位置
            availablePositions=((1<<n)-1)&(~(columns|diagonals1|diagonals2))
            while availablePositions:
                #获取最一个1的
                position=availablePositions&-availablePositions
                index=bin(position - 1).count("1")
                tmp="."*index+"Q"+"."*(n-index-1)
                helper(row+1,columns|position, (diagonals1|position)<<1 ,(diagonals2|position)>>1 ,path+[tmp])
                availablePositions=availablePositions&(availablePositions-1)
        #从第0行开始往下找
        helper(0,0,0,0,[])
        return res