[Luogu2730] 魔板 Magic Squares

Description

在魔方风靡全球之后，RUBIK先生发明了它的简化版——魔板

如上表所示，魔板由8个同样大小的方块组成，每个方块的颜色均不相同，本题中分别用数字1-8表示，它们可能出现在魔板的任一位置。任一时刻魔板的状态都可以用方块的颜色序列表示：从魔板的左上角开始，按顺时针方向依次写下各方块的颜色代号，得到数字序列即可表示此时魔板的状态。例如，序列（1、2、3、4、5、6、7、8）表示上表中魔板的状态，这也是本题中魔板的初始状态。对于魔板，可以施加三种不同操作，分别以A、B、C标识。具体操作如下：

A：上下行互换；

B：每一行同时循环右移一格；

C：中间4个方块顺时针旋转一格。

应用这三种基本操作，可以由任一状态达到任意另一状态。操作方法如下：

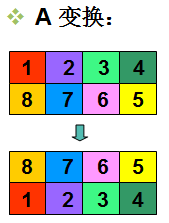
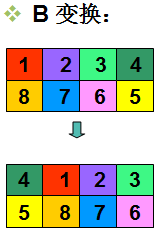
上表描述了上述3种操作的具体含义。表中方格外面的数字标识魔板的8个方块位置，方格内的数字表示此次操作前该方块所在位置。即：如果位置P中有数字I，则表示此次操作前方块所在位置I。

对于每种可能的状态，这三种基本操作都可以使用。

你要编程计算用最少的基本操作完成基本状态到目标状态的转换，输出基本操作序列。

Input

只有一行，包括8个整数，用空格分开（这些整数在范围 1—8 之间）不换行，表示目标状态。

Output

Line 1: 包括一个整数，表示最短操作序列的长度

Line 2: 在字典序中最早出现的操作序列，用字符串表示

Sample Input

2 6 8 4 5 7 3 1 

Sample Output

7 
BCABCCB

题解

这题很明显，是\(BFS\)，对于可能出现重复状态，我们需要判重，我用的是\(Hash\)中常用的康托展开

以下是康托展开部分

int Calc(node q)
{
	int Res=0,c;
	for(int i=1;i<8;++i)
	{
		c=0;
		for(int j=i+1;j<=8;++j)
			if(q.mp[i]<q.mp[j]) ++c;
		Res+=c*fac[8-i];
	}
	return Res;
}

还可以写成

int Calc(node q)
{
	int Res=0,c;
	for(int i=8;i>1;--i)
	{
		c=0;
		for(int j=1;j<i;++j)
			if(q.mp[i]<q.mp[j]) ++c;
		Res+=c*fac[i-1];
	}
	return Res;
}

但需要注意的是无论怎样做，都需要让可能大一些的\(c\)乘以大阶乘，因为这样才能避免重复，一把辛酸泪…

---

\(my~code\)

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<iomanip>
#include<vector>
#include<map>
#include<set>
#include<bitset>
using namespace std;

const int Max_Size=1e+6;
struct node
{
	int mp[9],cnt,nx;
	char c;
}Q[Max_Size];
int l,r;
int goal[9];
int fac[]={1,1,2,6,24,120,720,5040,40320};
int Hash[40321];

int Calc(node q)
{
	int Res=0,c;
	for(int i=1;i<8;++i)
	{
		c=0;
		for(int j=i+1;j<=8;++j)
			if(q.mp[i]<q.mp[j]) ++c;
		Res+=c*fac[8-i];
	}
	/*
	for(int i=8;i>1;--i)
	{
		c=0;
		for(int j=1;j<i;++j)
			if(q.mp[i]<q.mp[j]) ++c;
		Res+=c*fac[i-1];
	}
	*/
	return Res;
}

bool Check(node q)
{
	for(int i=1;i<=8;++i)
		if(q.mp[i]!=goal[i]) return 0;
	return 1;
}

void Output(int id)
{
	if(id==1) return;
	Output(Q[id].nx);
	printf("%c",Q[id].c);
}

void BFS()
{
	l=r=1;
	for(int i=1;i<=8;++i) Q[1].mp[i]=i;
	Q[1].cnt=0,Q[1].nx=-1,Hash[Calc(Q[1])]=1;
	node q; int tmp;
	while(l<=r)
	{
		if(Check(Q[l]))
		{
			printf("%d\n",Q[l].cnt),
			Output(l);
			return;
		}
		q=Q[l],++q.cnt,q.nx=l;
		//A
		for(int i=1;i<=8;++i) q.mp[i]=Q[l].mp[9-i];
		tmp=Calc(q);
		if(!Hash[tmp])
		{
			Hash[tmp]=1,q.c='A';
			++r,Q[r]=q;
		}
		//B
		q.mp[1]=Q[l].mp[4];
		for(int i=2;i<=4;++i) q.mp[i]=Q[l].mp[i-1];
		q.mp[8]=Q[l].mp[5];
		for(int i=5;i<=7;++i) q.mp[i]=Q[l].mp[i+1];
		tmp=Calc(q);
		if(!Hash[tmp])
		{
			Hash[tmp]=1,q.c='B';
			++r,Q[r]=q;
		}
		//C
		q.mp[1]=Q[l].mp[1],
		q.mp[4]=Q[l].mp[4],
		q.mp[5]=Q[l].mp[5],
		q.mp[8]=Q[l].mp[8],
		q.mp[2]=Q[l].mp[7],
		q.mp[3]=Q[l].mp[2],
		q.mp[6]=Q[l].mp[3],
		q.mp[7]=Q[l].mp[6],
		tmp=Calc(q);
		if(!Hash[tmp])
		{
			Hash[tmp]=1,q.c='C';
			++r,Q[r]=q;
		}
		++l;
	}
}

int main()
{
	for(int i=1;i<=8;++i) scanf("%d",&goal[i]);
	BFS();
	return 0;
}