CF27D

前言

其实这道题是可以不用 2-SAT 的但是我是从 2-SAT 题单中进来的所以还是使用了 2-SAT。

思路

其实可以发现对于一条边只可能出现两种情况在圈内和在圈外所以我们只需要想如何连边即可，首先判断出矛盾的情况，再连边最后跑一遍 Tarjan 即可。这里重点就在于如何判断矛盾情况，如下图就是矛盾情况。

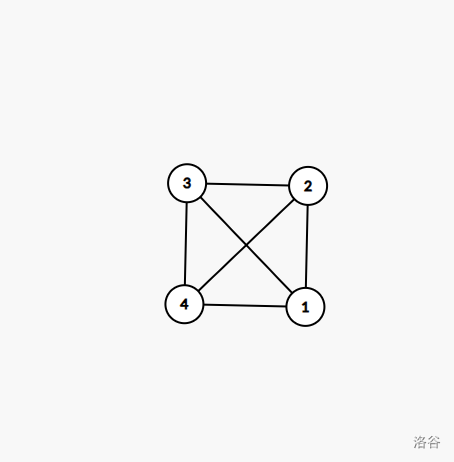
那么我们能得出结论如果两条边 \(i\) 和 \(j\) 矛盾，那么一定有 \(x_i<x_j<y_i<y_j\) 或者 \(x_j<x_i<y_j<y_i\) 这里只需要遍历 \(i\) 和 \(j\) 一遍和 \(j\) 和 \(i\) 一遍即可。

然后代码也就呼之欲出了。

代码

#include <bits/stdc++.h>
using namespace std ;
#define int long long
#define rep(i,x,y) for(int i=x;i<=y;i++)
#define rep1(i,x,y) for(int i=x;i>=y;i--)
#define fire signed
#define kong putchar(' ')
#define end putchar('\n')
#define in(x) scanf("%lld",&x)
#define lcm(x,y) x*y/__gcd(x,y)
#define pb push_back
#define il inline
il void print(int x) {
	if(x>=10) print(x/10);
	putchar(x%10+'0');
}
pair<int,int>p[222];
/*
1~m 选
m+1~2*m 不选 
*/
int n,m;
vector<int>v[222];
int dfn[201],low[201],is[210];
stack<int>s;
int idx,val[210],cnt;
void tarjan(int x) {
	low[x]=dfn[x]=++idx;
	s.push(x);
	is[x]=1;
	for(auto to:v[x]) {
		if(!dfn[to]) tarjan(to),low[x]=min(low[x],low[to]);
		else if(is[to]) low[x]=min(low[x],dfn[to]);
	}
	if(low[x]==dfn[x]) {
		int p;
		cnt++;
		do{
			p=s.top();
			s.pop();
			is[p]=false;
			val[p]=cnt;
		} while(p!=x);
	} 
}
fire main() {
	in(n),in(m);
	rep(i,1,m) in(p[i].first),in(p[i].second);
	rep(i,1,m) if(p[i].first>p[i].second) swap(p[i].first,p[i].second);
	rep(i,1,m) {
		rep(j,1,m) {
			if(p[i].first<p[j].first&&p[i].second>p[j].first&&p[i].second<p[j].second&&p[j].first<p[i].second) {
				v[i].push_back(j+m);
				v[i+m].push_back(j);
				v[j].push_back(i+m);
				v[j+m].push_back(i);
			}
		}
	}
	rep(i,1,2*m) if(!dfn[i]) tarjan(i);
	rep(i,1,m) {
		if(val[i]==val[i+m]) {
			puts("Impossible");
			return false;
		}
	}
	rep(i,1,m) {
		if(val[i]<val[i+m]) cout<<'o';
		else cout<<'i';
	}
	return false;
}
/*
5 3
4 2
1 3
5 2
*/