d2l-优化算法

1. 优化和深度学习

优化和深度学习的目标是不同的：

• 优化关注的是最小化目标
• 深度学习关注的是在给定有限数据量的情况下寻找合适的模型

例如：

• 优化问题的目标通常是减少训练误差。
• 深度学习的目标通常是减少泛化误差。为了实现该目标，除了使用优化算法，还需要注意过拟合。

1.1 局部最小值

深度学习模型的目标函数通常有许多局部最优解。随着目标函数解的梯度接近或变为0时，迭代可能会停止。
最终得到的数值解可能只是局部最优解，而非全局最优解。
一定程度的噪声可能会使参数跳出局部最小值，这是小批量随机梯度下降的优点之一。

1.2 鞍点

除了局部最小值，鞍点(saddle point)是梯度消失的另一个原因。
鞍点是指函数的所有梯度消失，但既不是全局最小值，也不是局部最小值的位置。
例如\(f(x) = x^3\)，在\(x = 0\)处，函数的一阶和二阶倒数消失。

• 一个问题可能有很多的鞍点，因为问题通常不是凸的。
• 梯度消失可能会导致优化停滞，重参数化通常会有所帮助。对参数进行良好的初始化也可能是有益的。

2. 梯度下降

2.1 梯度下降

最简单的迭代求解算法：

\[\mathbf{x}_t = \mathbf{x}_{t-1} - \eta \nabla{f(\mathbf{x}_{t-1})} \]

其中，\(\eta\)为学习率，选取合适的学习率很重要。

2.2 随机梯度下降 SGD

有\(n\)个样本时，每次计算\(f(x) = \frac{1}{n} \sum_{i=1}^{n}l_i(x)\)的导数，代价很大，时间复杂度为\(O(n)\)。

随机梯度下降：每次从数据样本中随机均匀采样一个索引\(i\)，并计算\(\nabla f_i(x)\)来更新\(x\)：

\[x \leftarrow x - \eta \nabla f_i(x) \]

时间复杂度从\(O(n)\)降为\(O(1)\)。
理论保证：随机梯度\(\nabla f_i(x)\)是对完整梯度\(\nabla f(x)\)的无偏估计

\[E[\nabla l_i (x)] = E[\nabla f(x)] \]

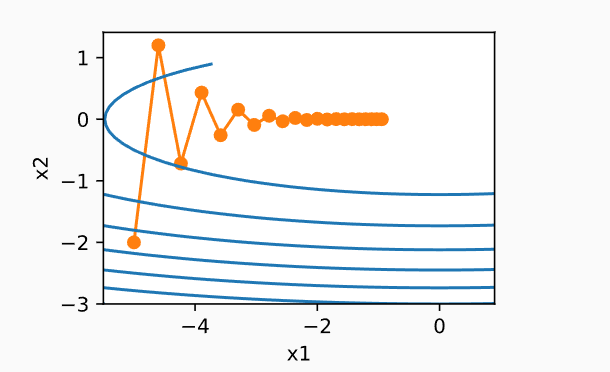
缺点：

• 由于梯度的随机性质，即使接近最小值，仍然受到单个样本点的瞬间梯度所注入的不确定性的影响。
• 选取合适的学习率对SGD仍然是一个重要的问题。

解决办法：在优化过程中动态降低学习率，例如：分段常数、指数衰减、多项式衰减（比较流行）。

2.3 小批量随机梯度下降

• 梯度下降：对所有样本点计算梯度是一件很贵的操作。
• 随机梯度下降：计算单样本的梯度难以完全利用硬件资源（GPU）
• 小批量计算梯度：两者的折中，能够提高计算效率。一般来说，小批量随机梯度下降比梯度下降和随机梯度下降的速度更快，收敛风险更小。

小批量随机梯度下降：在时间\(t\)采样一个随机子集\(I_t \in {1, \ldots, n}\)，使得\(\|I_t\| = b\)

\[x_t = x_{t-1} - \frac{\eta}{b}\nabla l_i(x_{t-1}) \]

同样，这是一个无偏近似，但标准差降低了\(b^{-\frac{1}{2}}\).

\[E[\frac{1}{b}\sum_{i \in I_t} \nabla l_i(x)] = \nabla f(x) \]

3. 动量法 Momentum

动量法使用平滑过的梯度对权重更新

\[g_t = \frac{1}{b} \sum_{i \in I_t}\nabla l_i(x_{t-1}) \]

\[v_t = \beta v_{t-1} + g_t \]

其中，\(\beta \in (0, 1)\)，\(v\)被称为动量(momentum)，它积累了过去的梯度。

递归地展开，可以写成：

\[v_t = g_t + \beta g_{t-1} + \beta^2 g_{t-2} + \beta^3 g_{t-3} + \ldots \]

\[x_t = x_{t-1} - \eta v_t \]

• \(\beta\)常见取值为[0.5, 0.9, 0.95, 0.99].
• 较大的\(\beta\)相当于长期平均值。新的梯度指向的是过去梯度的加权平均值的方向。

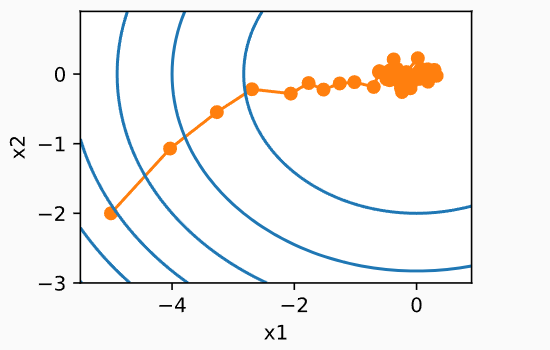
下面考虑一个函数 \(f(x) = 0.1 x_1^2 + 2x_2^2\)

梯度下降法：由于\(x_2\)方向的梯度比\(x_1\)方向的梯度大得多，变化也快得多。

• 如果学习率较小，\(x_1\)方向移动缓慢。
• 如果学习率较大，\(x_2\)方向会发散。

动量法：

• 在\(x_1\)方向，会聚合非常对齐的梯度，从而增加每一步覆盖的距离。
• 在\(x_2\)方向，由于上下振荡会互相抵消，聚合梯度将减小步长大小。

下面是\(\beta = 0.5\)的优化图，如果\(\beta=0\)则退化为梯度下降法。

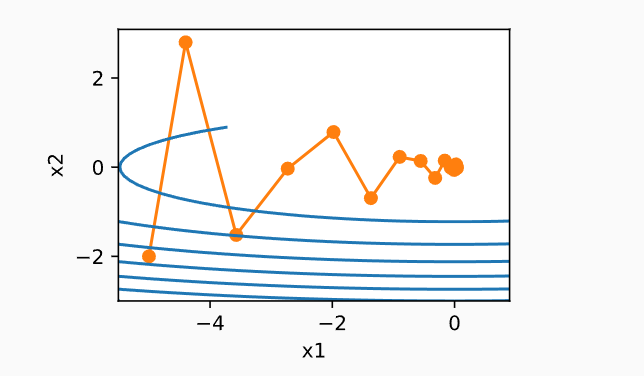
• 对于无噪声梯度下降和嘈杂随机梯度下降，动量法都是可取的。

4. Adam算法

Adam集成了之前许多优化算法的技术，是一个很流行的学习算法。

• Adam对学习率\(\eta\)没有那么敏感。
• 对于具有显著差异的梯度，可能会遇到收敛性问题。可以通过使用更大的小批量或者切换到改进的估计值\(s_t\)来修正。Yogi提供了这样的替代方案。