d2l-注意力机制

1. 注意力提示

人的注意力是有限的、有价值和稀缺的资源
受试者使用非自主性和自主性提示有选择性地引导注意力。前者基于突出性，后者则依赖于意识。

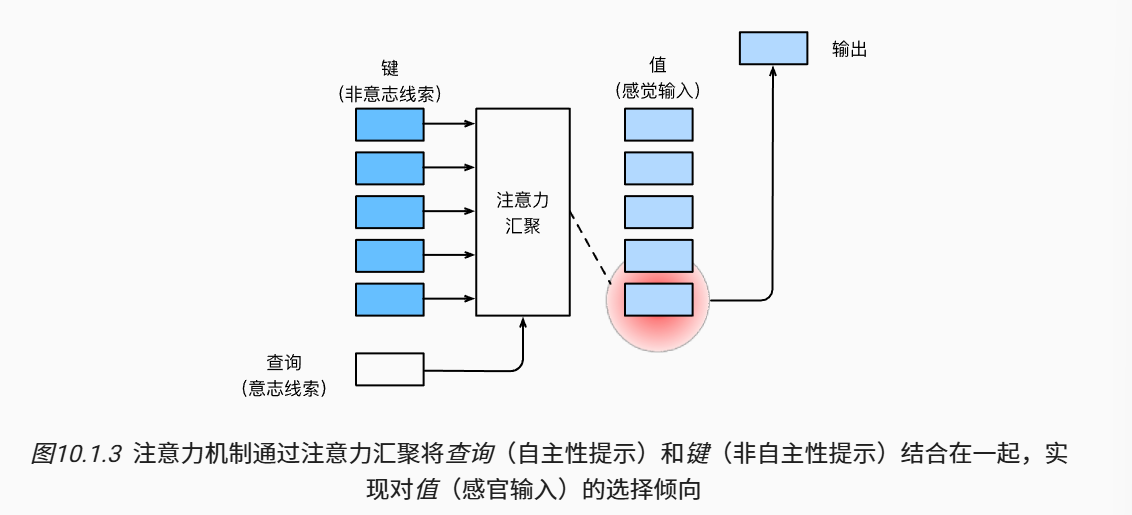
• 注意力机制与全连接层或汇聚层的区别在于增加的自主提示(query)。
• 注意力机制通过注意力汇聚是实现对值(value)的偏向性选择，其中包含查询（自主性提示）和键（非自住性提示）。
• 可以通过热图(heat map)对注意力进行可视化。

2. 注意力汇聚：Nadaraya-Watson 核回归

2.1 平均汇聚

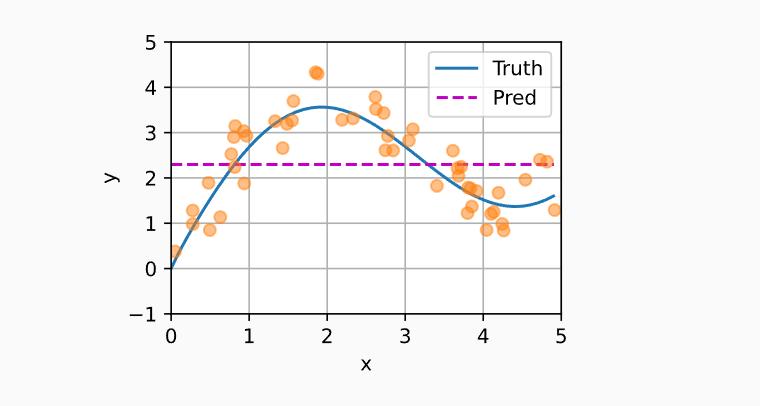
平均汇聚是一种最简单的估计器

\[f(x) = \frac{1}{n}\sum_{i=1}^{n}y_i \]

这个估计器的效果不佳。

2.2 非参数注意力汇聚

平均汇聚没有考虑输入\(x_i\)。1964年，Nadaraya和Watson根据输入位置对输出\(y_i\)进行加权：

\[f(x) = \sum_{i=1}^{n} \frac{K(x-x_i)}{\sum_{j=1}^{n} K(x-x_j)}y_i \]

其中，\(K\)称为核，是一种函数。

如果采用高斯核(Gaussian kernel)：\(K(u) = \frac{1}{\sqrt{2\pi}}exp(-\frac{u^2}{2})\)
带入到式子中，可以得到：

\[f(x) = \sum_{i=1}^{n} softmax(-\frac{1}{2}(x - x_i)^2)y_i \]

• 直观的理解：\(x_i\)越接近\(x\)，\(y_i\)被分配到的注意力权重更大

可以从注意力机制框架的角度重写称为一个更通用的形式，注意力汇聚 (attention pooling)公式：

\[f(x) = \alpha(x, x_i)y_i \]

• \(\alpha(x, x_i)\)被称为注意力权重，权重被分配给每个对应值\(y_i\)
• 对于任何查询，模型在所有键值对注意力权重都是一个有效的概率分布：
  • 它们是非负的
  • 总和为1

2.3 带参数注意力汇聚

非参数的Nadaraya-Watson核回归具有一致性：如果有足够的数据，模型会收敛到最优结果。

但是，现实中往往没有足量的数据，可以将可学习参数加入到注意力汇聚中，加速模型的拟合。

\[f(x) = \sum_{i=1}^{n} softmax(-\frac{1}{2}((x - x_i)\omega)^2)y_i \]

3. 注意力评分函数

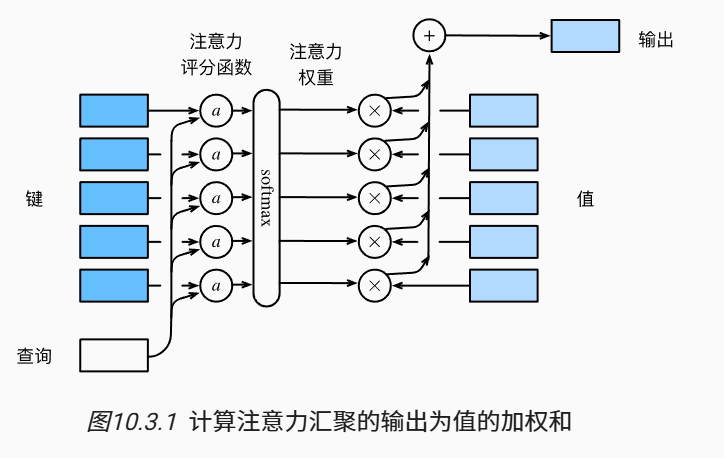
• softmax之前的是注意力分数 score
• softmax之后的是注意力权重 weight 表示概率分布
• 注意力汇聚输出的是加权和

假设有1个查询\(\mathbf{q} \in R^q\)和\(m\)个键值对，其中k和v的长度分别为\(\mathbf{k_i} \in R^k\), \(\mathbf{v_i} \in R_v\)

\[f(\mathbf{q}, (\mathbf{k}_1, \mathbf{v}_1), ..., (\mathbf{k}_m, \mathbf{v}_m)) = \sum_{i=1}^m\alpha(\mathbf{q}, \mathbf{k}_i)\mathbf{v}_i \in R^v \]

其中，

\[\alpha(\mathbf{q}, \mathbf{k}_i) = softmax(a(\mathbf{q}, \mathbf{k}_i)) = \frac{exp(a(\mathbf{q}, \mathbf{k}_i))}{\sum_{j=1}^m exp(a(\mathbf{q}, \mathbf{k}_j))} \in R \]

• \(\alpha\)是注意力权重，为标量
• \(f\)的输出为预测的value，长度为\(v\)

本节将介绍2种注意力的计算方法：加性注意力、缩放点积注意力。

3.1 masked_softmax

为了仅在有意义的词元上作注意力汇聚，可以指定一个valid_len，在计算softmax的时候过滤掉超出范围的内容。
任何超出范围的位置都被置为0.

def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
                              value=-1e6)
        return nn.functional.softmax(X.reshape(shape), dim=-1)

3.2 加性注意力

当查询(query)和键(key)是长度不同的向量时，可以使用加性注意力。加性注意力的评分函数为

\[a(\mathbf{q}, \mathbf{k}) = \mathbf{w}_v^{\top} tanh(\mathbf{W}_q\mathbf{q} + \mathbf{W}_k\mathbf{k}) \in R \]

其中，可学习的参数为\(\mathbf{W}_q \in R^{h * q}\), \(\mathbf{W}_k \in R^{h * k}\), \(\mathbf{w}_v \in R^h\)。

相当于将query和key拼接后输入到单隐藏层的mlp中，隐藏单元个数为h，激活函数为tanh，不使用bias。

class AdditiveAttention(nn.Module):
    """加性注意力"""
    def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
        self.w_v = nn.Linear(num_hiddens, 1, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, queries, keys, values, valid_lens):
        queries, keys = self.W_q(queries), self.W_k(keys)
        # 在维度扩展后，
        # queries的形状：(batch_size，查询的个数，1，num_hidden)
        # key的形状：(batch_size，1，“键－值”对的个数，num_hiddens)
        # 使用广播方式进行求和
        features = queries.unsqueeze(2) + keys.unsqueeze(1)
        features = torch.tanh(features)
        # self.w_v仅有一个输出，因此从形状中移除最后那个维度。
        # scores的形状：(batch_size，查询的个数，“键-值”对的个数)
        scores = self.w_v(features).squeeze(-1)
        self.attention_weights = masked_softmax(scores, valid_lens)
        # values的形状：(batch_size，“键－值”对的个数，值的维度)
        return torch.bmm(self.dropout(self.attention_weights), values)

查询、键和值的形状为（批量大小，步数或词元序列长度，特征大小），假设

• 查询的形状为(2, 1, 20)
• 键的形状为(2, 10, 2)
• 值的形状为(2, 10 ,4)

则注意力汇聚(attention pooling)的输出的形状为(2, 1, 4)。(batch_size, num_query, value_len)

3.3 缩放点积注意力

如果query和key的长度相同，都为\(d\)，则可以使用缩放点积注意力，计算效率更高。

缩放点积注意力(scaled dot-product attention)评分函数：

\[a(\mathbf{q}, \mathbf{k}) = \frac{\mathbf{q}^\top \mathbf{k}}{\sqrt{d}} \]

缩放点积注意力为：

\[softmax(\frac{\mathbf{q}^\top \mathbf{k}}{\sqrt{d}})\mathbf{V} \in R^{n * v} \]

可以通过dropout 对模型正则化。

class DotProductAttention(nn.Module):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        d = queries.shape[-1]
        # 设置transpose_b=True为了交换keys的最后两个维度
        scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
        self.attention_weights = masked_softmax(scores, valid_lens)
        return torch.bmm(self.dropout(self.attention_weights), values)

4. 使用注意力机制的seq2seq模型 (Bahdanau 注意力)

机器翻译中，每个生成的词可能像关于源句子中的不同的词。

• 之前讲的seq2seq，在每个解码步骤中都使用相同的上下文变量
• Bahdanau等人提出，如果不是所有输入词元都相关，模型将仅对齐输入序列中与当前预测相关的部分。

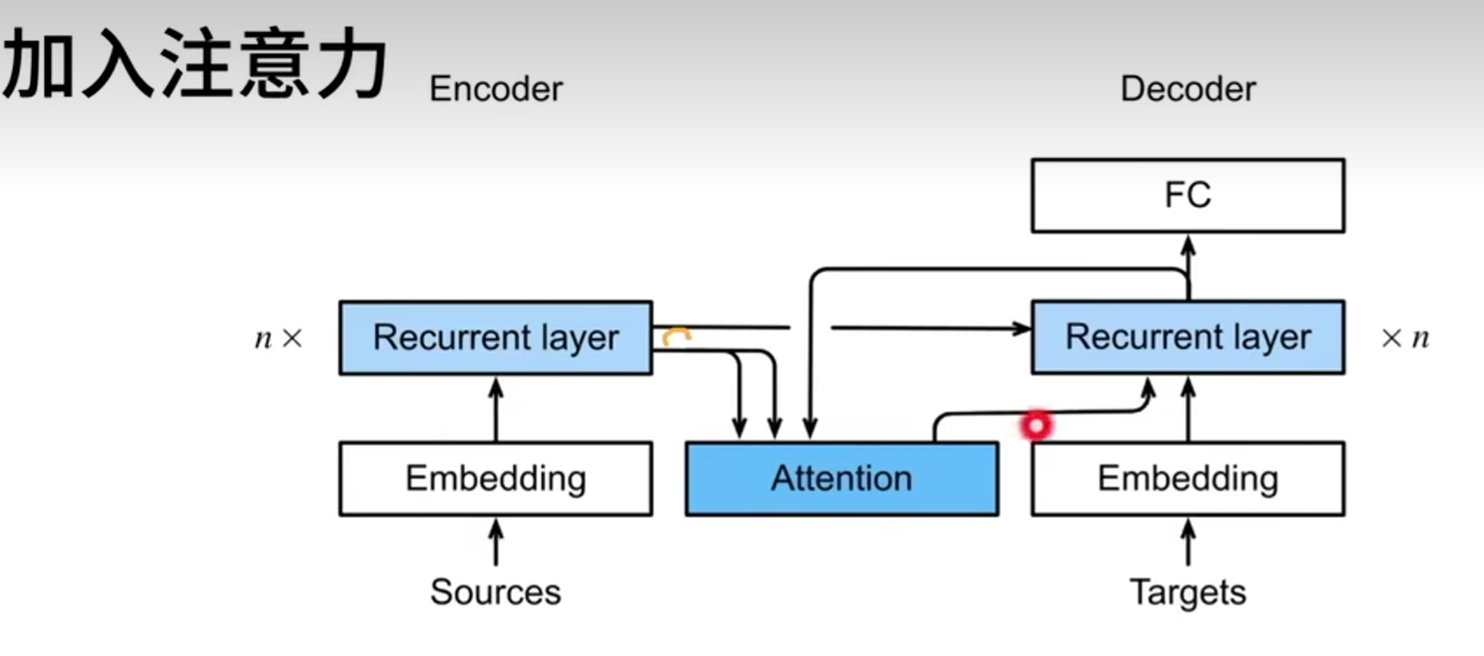
• 编码器对每次词的输出作为key和value(它们是一样的)
• 解码器RNN对上一个词的输出是query
• 注意力的输出和下一个词的embedding合并进入RNN
• 注意力机制考验根据解码器RNN的输出来匹配到合适的编码器RNN的输出来更有效的传递信息。

编码器不变，需要修改解码器

class Seq2SeqAttentionDecoder(AttentionDecoder):
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0, **kwargs):
        super(Seq2SeqAttentionDecoder, self).__init__(**kwargs)
        self.attention = d2l.AdditiveAttention(
            num_hiddens, num_hiddens, num_hiddens, dropout)
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(
            embed_size + num_hiddens, num_hiddens, num_layers,
            dropout=dropout)
        self.dense = nn.Linear(num_hiddens, vocab_size)

    def init_state(self, enc_outputs, enc_valid_lens, *args):
        # outputs的形状为(batch_size，num_steps，num_hiddens).
        # hidden_state的形状为(num_layers，batch_size，num_hiddens)
        outputs, hidden_state = enc_outputs
        return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)

    def forward(self, X, state):
        # enc_outputs的形状为(batch_size,num_steps,num_hiddens).
        # hidden_state的形状为(num_layers,batch_size,
        # num_hiddens)
        enc_outputs, hidden_state, enc_valid_lens = state
        # 输出X的形状为(num_steps,batch_size,embed_size)
        X = self.embedding(X).permute(1, 0, 2)
        outputs, self._attention_weights = [], []
        for x in X:
            # query的形状为(batch_size,1,num_hiddens)
            query = torch.unsqueeze(hidden_state[-1], dim=1)
            # context的形状为(batch_size,1,num_hiddens)
            context = self.attention(
                query, enc_outputs, enc_outputs, enc_valid_lens)
            # 在特征维度上连结
            x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
            # 将x变形为(1,batch_size,embed_size+num_hiddens)
            out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
            outputs.append(out)
            self._attention_weights.append(self.attention.attention_weights)
        # 全连接层变换后，outputs的形状为
        # (num_steps,batch_size,vocab_size)
        outputs = self.dense(torch.cat(outputs, dim=0))
        return outputs.permute(1, 0, 2), [enc_outputs, hidden_state,
                                          enc_valid_lens]

    @property
    def attention_weights(self):
        return self._attention_weights

训练模型

embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10
lr, num_epochs, device = 0.005, 250, d2l.try_gpu()

train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = d2l.Seq2SeqEncoder(
    len(src_vocab), embed_size, num_hiddens, num_layers, dropout)
decoder = Seq2SeqAttentionDecoder(
    len(tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
net = d2l.EncoderDecoder(encoder, decoder)
d2l.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)

5. 自注意力和位置编码

给定词元序列\(x_1, x_2, ... ,x_n\)，其中\(x_i \in R^d\)。即序列长度为\(n\)，每个词元的维度为\(d\)。
自注意力输出为一个长度为\(n\)的序列\(y_1, y_2, ... , y_n\)，其中：

\[y_i = f(x_1, (x_1, x_1), ..., (x_n, x_n)) \]

• 自注意力池化层将\(x_i\)当作key, value, query来对序列抽取特征

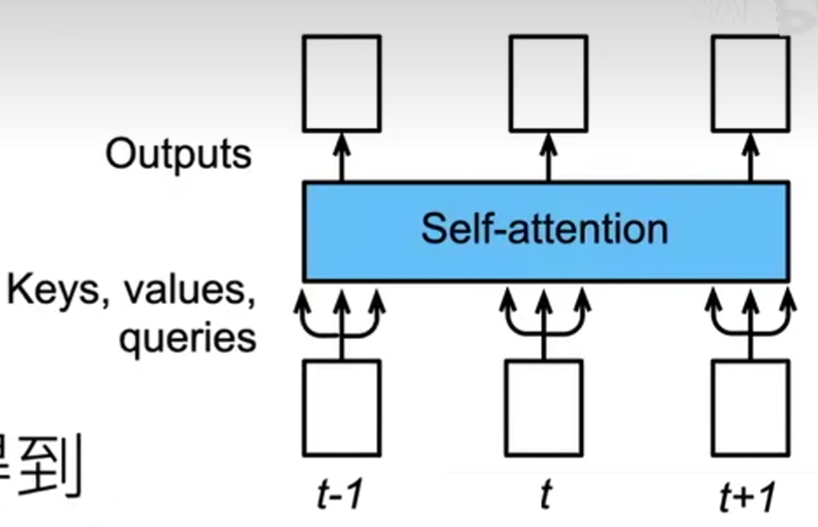
5.1 CNN、RNN和self-attention的比较

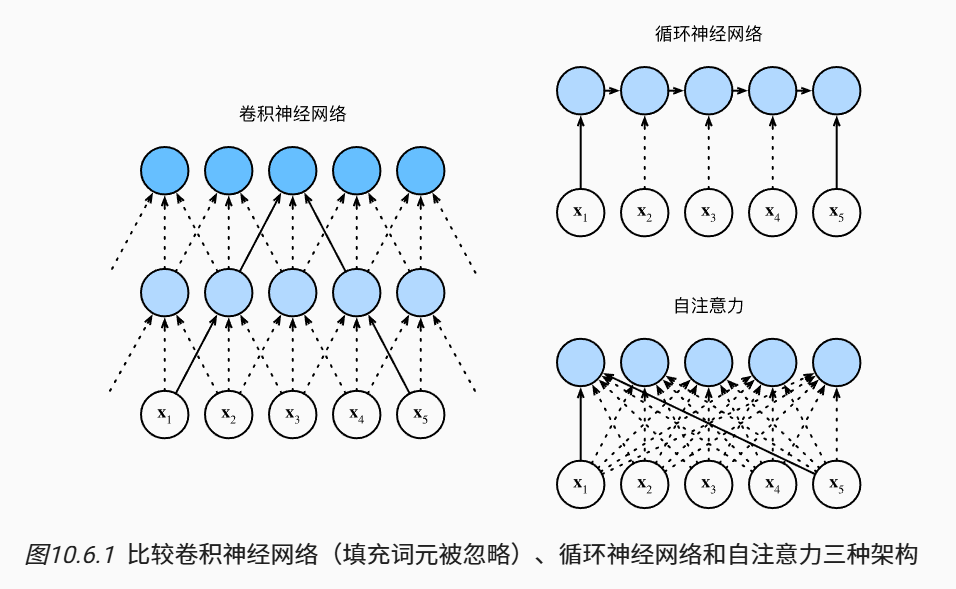
	CNN	RNN	self-attention
计算复杂度	\(O(knd^2)\)	\(O(nd^2)\)	\(O(n^2d)\)
并行度	\(O(n)\)	\(O(1)\)	\(O(n)\)
最长路径	\(O(\frac{n}{k})\)	\(O(n)\)	\(O(1)\)

• \(n\)为序列的长度，\(k\)为CNN的窗口大小，\(d\)为词元的维度。
• self-attention在处理长序列时（\(n\)很大时），计算复杂度高。
• CNN和self-attention的并行度好；RNN由于顺序操作，并行度不好。
• 任何的序列位置组合之间的路径越短，能更轻松地学习序列中的远距离依赖关系。

5.2 位置编码 (positional encoding)

为了使用序列的顺序信息，可以通过在输入表示中添加位置编码，来注入绝对的或相对的位置信息。
位置编码

• 可以通过学习得到
• 也可以通过公式得到固定位置编码

下面介绍的是基于正弦函数和余弦函数的固定位置编码。

• 假设输入\(X \in R^{n \times d}\)，则位置编码为形状相同的矩阵，即\(P \in R^{n \times d}\)。输入为\(X + P\).

位置编码 \(P\)矩阵 的第\(i\)行、第\(2j\)列和第\(2j+1\)列上的元素为：

\[p_{i, 2j} = sin(\frac{i}{10000^{2j/d}}) \]

\[p_{i, 2j+1} = cos(\frac{i}{10000^{2j/d}}) \]

除了绝对位置信息，上述固定编码还能学习到输入序列中的相对位置信息。
给定位置偏移\(\delta\)，位置\(i + \delta\)的位置编码可以通过位置\(i\)处的位置编码进行线性变换得到。

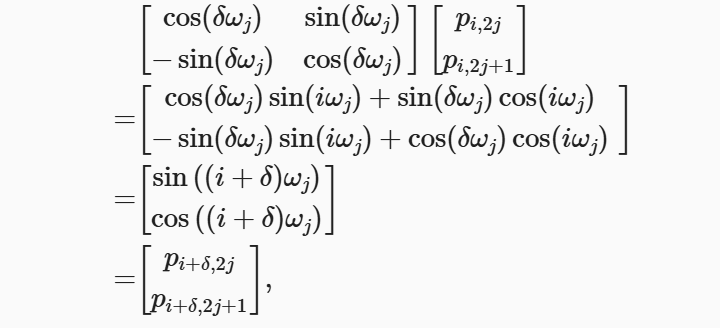
6. 多头注意力 (multihead attention)

给定相同的key, value, query时，我们希望基于相同的注意力机制学习到不同的行为，然后将不同的行为作为知识组合起来（如短距离依赖、长距离依赖）。
这些知识的不同来源于相同query, key, value的不同的子空间表示(representation subspaces)。

• 独立学习得到\(h\)组不同的线性投影(linear projections)来变换key, value, query
• 将这\(h\)组变换后的key, value, query并行地送入注意力汇聚
• 最后将注意力汇聚地输出拼接到一起，再送入一个全连接层

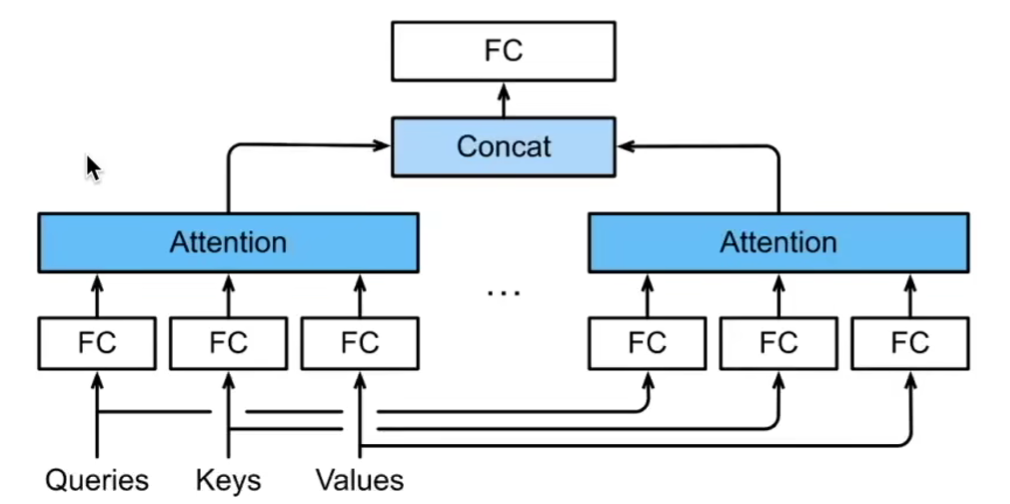
每个注意力头\(h_i (i = 1, ..., h)\)的计算方式：

\[h_i = f(W_i^{(q)}q, W_i^{(k)}k, W_i^{(v)}v) \in R^{p_v} \]

• query, key, value的维度分别是：\(d_q, d_k, d_v\).
• 可学习参数\(W_i^{(q)}, W_i^{(k)}, W_i^{(v)}\)的维度分别是\(p_q \times d_q, p_k \times d_k, p_v \times d_v\).
• \(f\)为注意力汇聚，如加性注意力、缩放点积注意力

将\(h\)个头输出拼接(concat)之后，再通过一个全连接层，可以得到多头注意力的输出。

\[W_o \begin{bmatrix} h_1 \\ h_2 \\ ... \\ h_h\end{bmatrix} \in R^{p_o} \]

• 通常选用缩放点积注意力作为注意力头
• 为了并行计算\(h\)个头，全连接层的维度通常选择为\(p_q \cdot h = p_k \cdot h = p_v \cdot h = p_o\).
• 在下面的实现中，通过num_hiddens指定\(p_o\)

class MultiHeadAttention(nn.Module):
    """多头注意力"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 num_heads, dropout, bias=False, **kwargs):
        super(MultiHeadAttention, self).__init__(**kwargs)
        self.num_heads = num_heads
        self.attention = d2l.DotProductAttention(dropout)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
        self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)

    def forward(self, queries, keys, values, valid_lens):
        # queries，keys，values的形状:
        # (batch_size，查询或者“键－值”对的个数，num_hiddens)
        # valid_lens　的形状:
        # (batch_size，)或(batch_size，查询的个数)
        # 经过变换后，输出的queries，keys，values　的形状:
        # (batch_size*num_heads，查询或者“键－值”对的个数，
        # num_hiddens/num_heads)
        queries = transpose_qkv(self.W_q(queries), self.num_heads)
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads)

        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次，
            # 然后如此复制第二项，然后诸如此类。
            valid_lens = torch.repeat_interleave(
                valid_lens, repeats=self.num_heads, dim=0)

        # output的形状:(batch_size*num_heads，查询的个数，
        # num_hiddens/num_heads)
        output = self.attention(queries, keys, values, valid_lens)

        # output_concat的形状:(batch_size，查询的个数，num_hiddens)
        output_concat = transpose_output(output, self.num_heads)
        return self.W_o(output_concat)

def transpose_qkv(X, num_heads):
    """为了多注意力头的并行计算而变换形状"""
    # 输入X的形状:(batch_size，查询或者“键－值”对的个数，num_hiddens)
    # 输出X的形状:(batch_size，查询或者“键－值”对的个数，num_heads，
    # num_hiddens/num_heads)
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)

    # 输出X的形状:(batch_size，num_heads，查询或者“键－值”对的个数,
    # num_hiddens/num_heads)
    X = X.permute(0, 2, 1, 3)

    # 最终输出的形状:(batch_size*num_heads,查询或者“键－值”对的个数,
    # num_hiddens/num_heads)
    return X.reshape(-1, X.shape[2], X.shape[3])

def transpose_output(X, num_heads):
    """逆转transpose_qkv函数的操作"""
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    X = X.permute(0, 2, 1, 3)
    return X.reshape(X.shape[0], X.shape[1], -1)

最终输出的形状为(batch_size, num_queries, num_hiddens).