d2l-GRU-LSTM

1. 门控循环单元 GRU

GRU和RNN的区别：

• GRU支持对隐状态的门控。模型有专门的机制来决定何时更新隐状态，何时重置隐状态
• GRU的数值稳定性更强，能够处理更长的文本
• GRU的功能是LSTM的变种，两者功能类似

重置门 (reset gate)，更新门 (update gate)：这两个门和隐状态的形状相同，因此GRU的可学习参数是RNN的3倍。

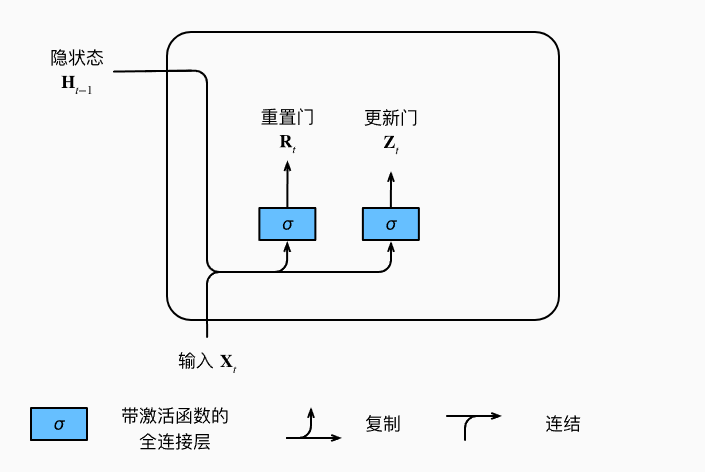
$$R_t=\sigma (X_t{W}_{xr}+H_{t-1}{W}_{hr}+b_r)$$

$$Z_t=\sigma (X_t{W}_{xz}+H_{t-1}{W}_{hz}+b_z)$$

其中，$\sigma$为sigmoid激活函数

候选隐状态 (candidate hidden state)：由重置门$R_t$与常规隐状态更新机制集成得到

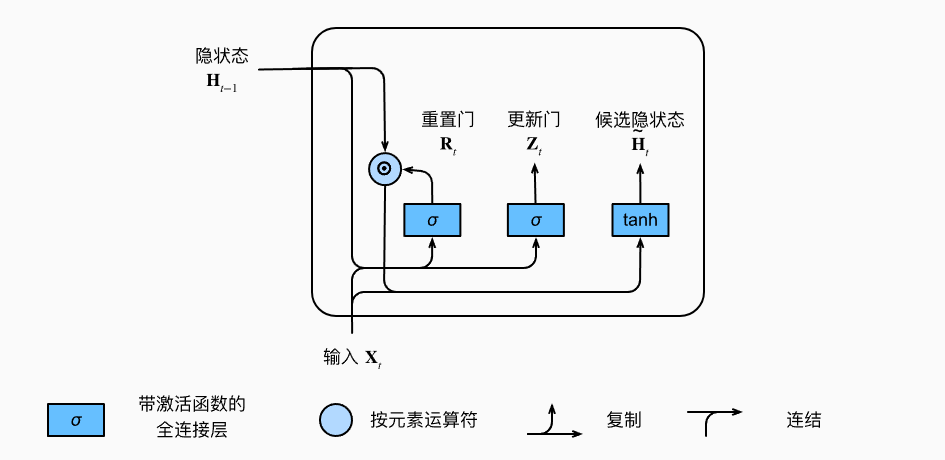
$${\tilde{H}}_t=tanh(X_t{W}_{xh}+(R_t\odot H_{t-1})W_{hh}+b_h)$$

其中，$\odot$为Hadamard积（按元素乘积）。

• $R_t$接近1时，类似于普通的RNN
• $R_t$接近0时，${\tilde{H}}_t$ 是以 $X_t$ 为输入的多层感知机的结果。先前的隐状态被重置为默认值。

隐状态$H_t$还取决于$H_{t-1}$, ${\tilde{H}}_t$, 更新门$Z_t$。

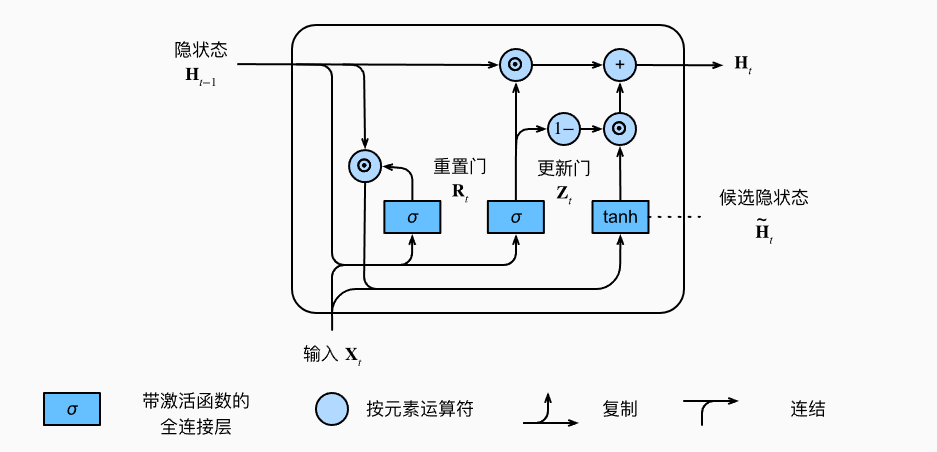
$$H_t=Z_t\odot H_{t-1}+(1-Z_t)\odot {\tilde{H}}_t$$

• $Z_t$接近1时，模型倾向于保留就状态，从而忽略$X_t$的信息
• $Z_t$接近0时，新的隐状态$H_t$接近候选状态${\tilde{H}}_t$

# Pytorch 简洁实现
num_inputs = vocab_size
gru_layer = nn.GRU(num_inputs, num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

综上所述：

• 重置门有助于模型捕获序列中的短期依赖关系
• 更新门有助于模型捕获序列中的长期依赖关系

2. 长短期记忆网络 LSTM

LSTM中有3种门：遗忘门 F，输入门 I，输出门 O

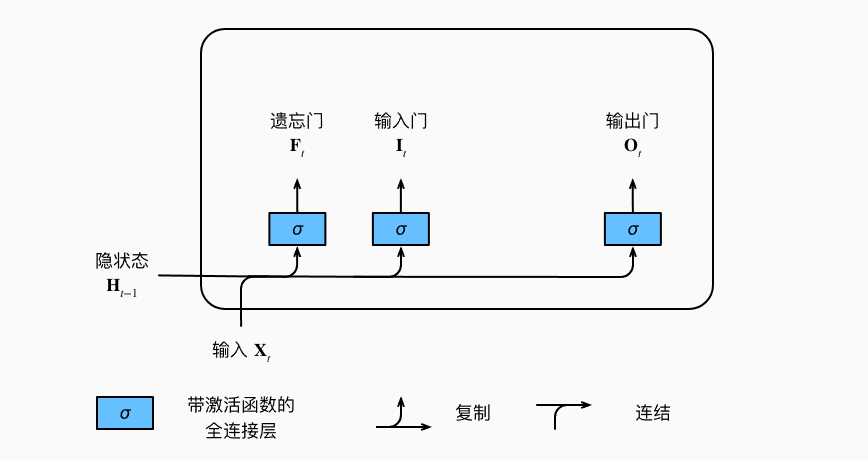
$$I_t=\sigma (X_t{W}_{xi}+H_{t-1}{W}_{hi}+b_i)$$

$$F_t=\sigma (X_t{W}_{xf}+H_{t-1}{W}_{hf}+b_f)$$

$$O_t=\sigma (X_t{W}_{xo}+H_{t-1}{W}_{ho}+b_o)$$

其中，$\sigma$为sigmoid激活函数

候选记忆元${\tilde{C}}_t$使用tanh作为激活函数。

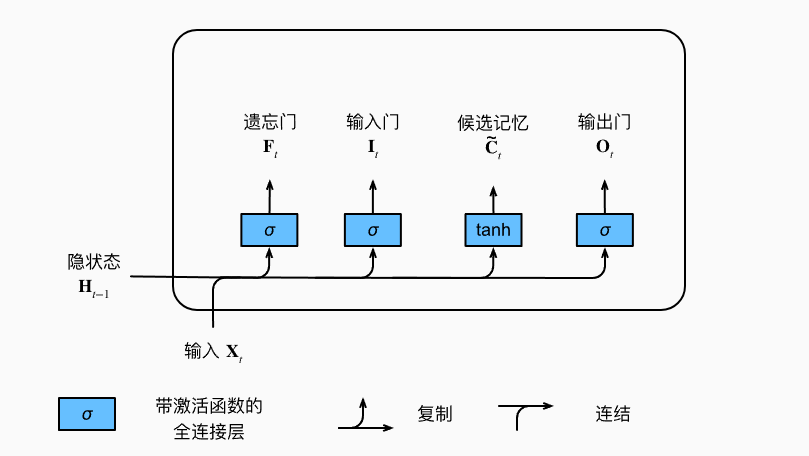
$${\tilde{C}}_t=tanh(X_t{W}_{xc}+H_{t-1}{W}_{hc}+b_c)$$

记忆元$C_t$：

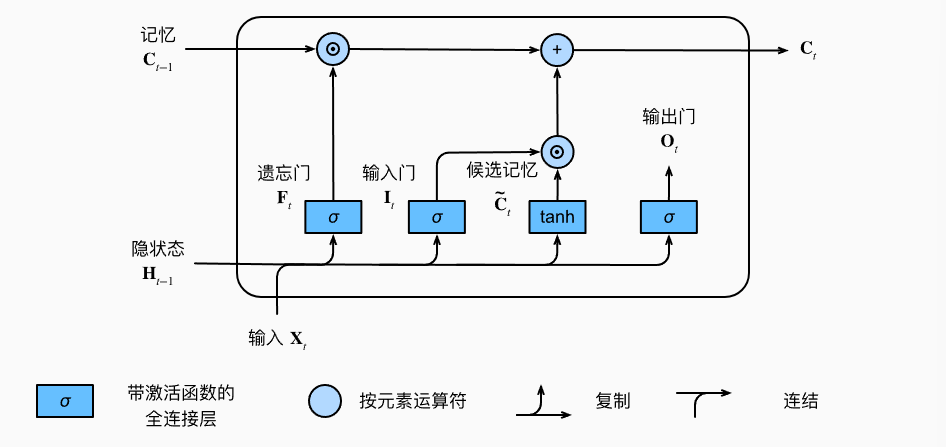
$$C_t=F_t\odot C_{t-1}+I_t\odot {\tilde{C}}_t$$

• 遗忘门$F_t$控制保留过去多少的记忆元 $C_{t-1}$
• 输入门$I_t$控制采用多少来自${\tilde{C}}_t$的新数据

隐状态$H_t$：

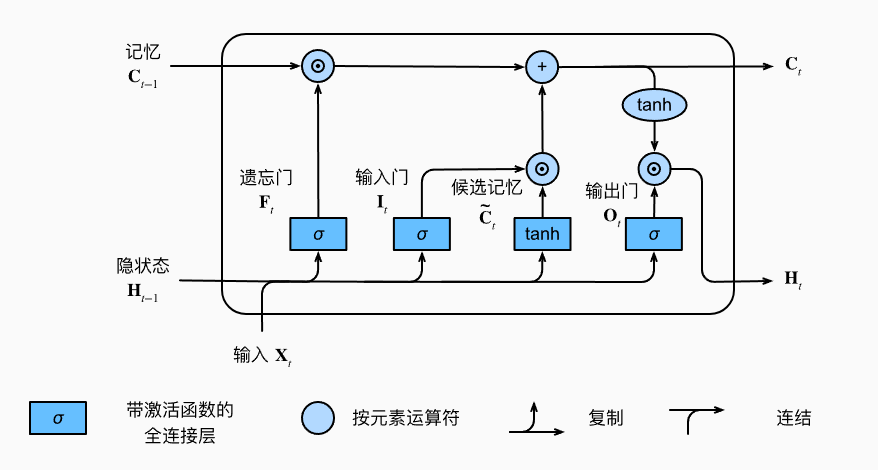
$$H_t=O_t\odot tanh(C_t)$$

• tanh函数保证了$H_t$始终在(-1, 1)内，防止梯度爆炸
• 输出门$O_t$接近1时，能够将所有记忆传递给预测部分
• 输出门$O_t$接近0时，只保留记忆元内的信息，而不更新隐状态

综上所述：

• LSTM中有3种门：遗忘门、输入门、输出门
• LSTM的隐藏层输出包括：
  1. 隐状态H：会传递到输出层
  2. 记忆元C：属于内部信息