d2l-循环神经网络
1. 序列模型
之前讨论的表格数据和图像数据,我们都默认数据来自于某种分布,并且所有样本都是独立同分布的(independently and identically distributed, i.i.d.).
然而,大部分数据并非如此。例如:文章中的单词、视频中的图像帧、对话中的音频信号、网站上的浏览行为
都是有顺序的。因此针对此类数据设计特定模型,可能效果会更好。
同时,我们不仅需要可以接收一个序列作为输入,还希望能够继续预测序列的后续。例如预测股市的波动、患者的体温曲线。
- 卷积神经网络 -> 空间信息
- 循环神经网络 -> 序列信息
- 自回归模型:使用自身过去数据来预测未来
- 马尔可夫模型:假设当前只跟最近少数数据(\(\tau\)个)相关,从而简化模型
- \(p(x_t | x_1, ..., x_{t-1}) = p(x_t | x_{t-\tau}, ..., x_{t-1}) = p(x_t | f(x_{t-\tau}, ..., x_{t-1}))\)
- 潜变量模型:使用潜变量\(h_t\)来概括历史信息
- \(h_t = f(x_1, ..., x_{t-1})\)
- \(x_t = p(x_t | h_t)\)
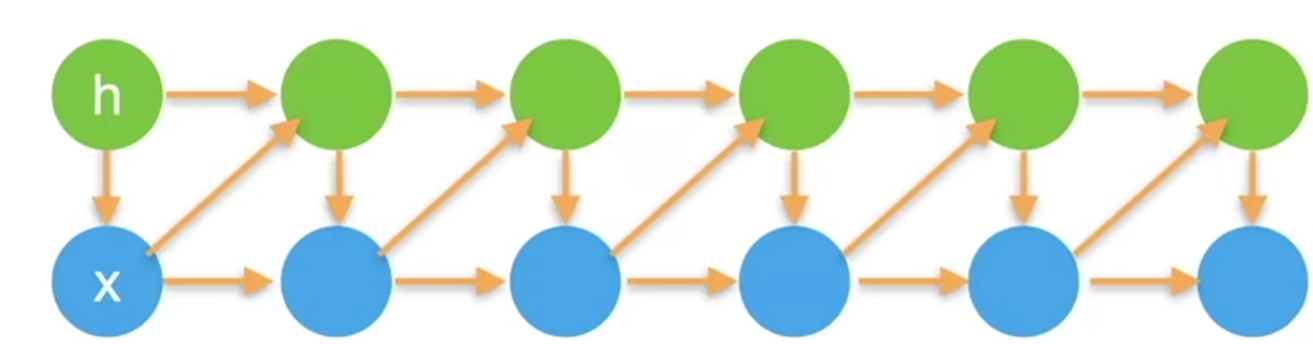
潜变量(latent variable)和隐变量(hidden variable):通常认为
- 隐变量(hidden variable)是现实生活中存在的,但是没有被观察到。
- 潜变量(latent variable)包含隐变量,潜变量可能在现实中不存在,例如标签信息。
- 在神经网络领域,两者有时会混用。
2. 文本预处理
文本预处理的常见步骤:
- 读取数据集:将文本作为字符串加载进内存
- 词元化:将字符串拆分为
词元 token(如单词或字符) - 词表 vocabulary:将词元映射到从0开始的数字索引上
- 对训练集中的文档合并,对唯一词元进行统计,统计结果称为
语料 corpus - 根据词元出现的频率,分配数字索引
- 很少出现的词元会被移除,用
<unk>记录
- 对训练集中的文档合并,对唯一词元进行统计,统计结果称为
- 将文本转化为数字索引序列,方便模型操作
3. 语言模型
自然语言统计
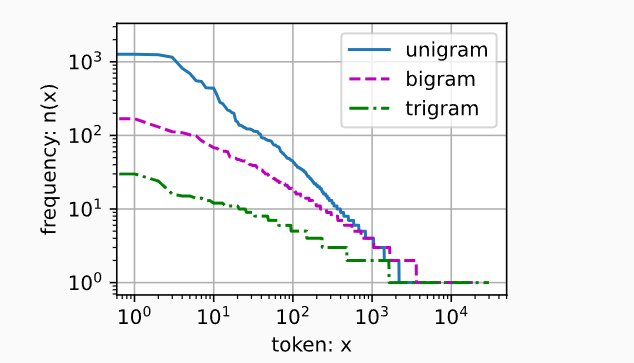
- 单词的频率满足
齐普夫定律 (Zipf's law),第\(i\)个最常用单词的频率\(n_i\)为:$ n_i \propto \frac{1}{i^\alpha}$ - n元组也遵循齐普夫定律。
- n元组的数量没有那么大,说明语言中存在相当多的结构。
读取长序列数据
数据与标签:对于语言建模,目标时基于目前为止看到的词元来预测下一个词元,因此标签是移位了一个词元的原始序列。
- 随机采样:确定
num_steps,每次随机丢弃开头的0 - num_steps-1个token- 相邻两个batch在原始序列上不一定相邻
X: tensor([[13, 14, 15, 16, 17],
[28, 29, 30, 31, 32]])
Y: tensor([[14, 15, 16, 17, 18],
[29, 30, 31, 32, 33]])
X: tensor([[ 3, 4, 5, 6, 7],
[18, 19, 20, 21, 22]])
Y: tensor([[ 4, 5, 6, 7, 8],
[19, 20, 21, 22, 23]])
X: tensor([[ 8, 9, 10, 11, 12],
[23, 24, 25, 26, 27]])
Y: tensor([[ 9, 10, 11, 12, 13],
[24, 25, 26, 27, 28]])
- 顺序采样:同样是随机丢弃开头的
0 - num_steps-1个token- 相邻两个batch在原始序列上是相邻的。
X: tensor([[ 0, 1, 2, 3, 4],
[17, 18, 19, 20, 21]])
Y: tensor([[ 1, 2, 3, 4, 5],
[18, 19, 20, 21, 22]])
X: tensor([[ 5, 6, 7, 8, 9],
[22, 23, 24, 25, 26]])
Y: tensor([[ 6, 7, 8, 9, 10],
[23, 24, 25, 26, 27]])
X: tensor([[10, 11, 12, 13, 14],
[27, 28, 29, 30, 31]])
Y: tensor([[11, 12, 13, 14, 15],
[28, 29, 30, 31, 32]])
4. 循环神经网络 RNN
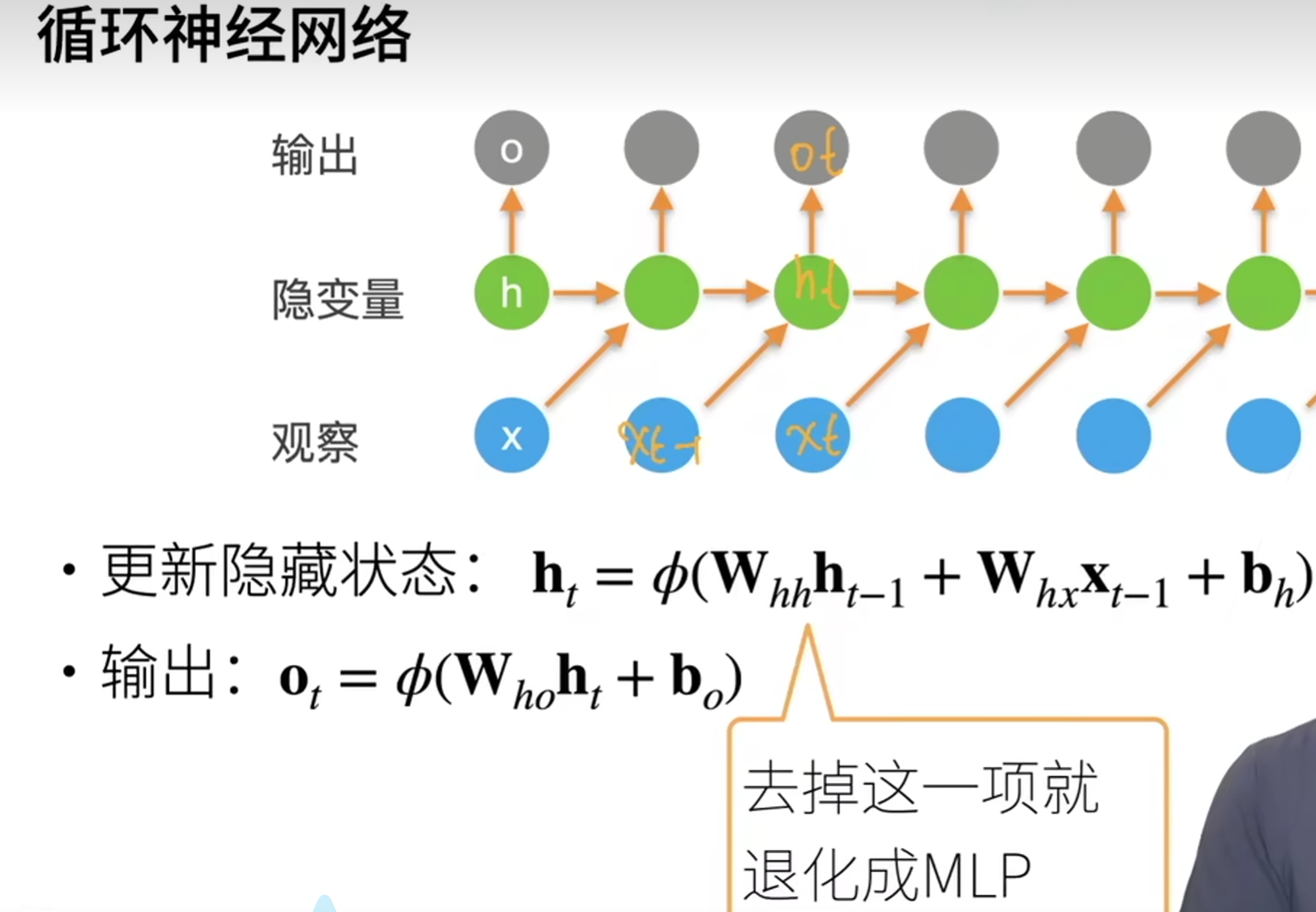
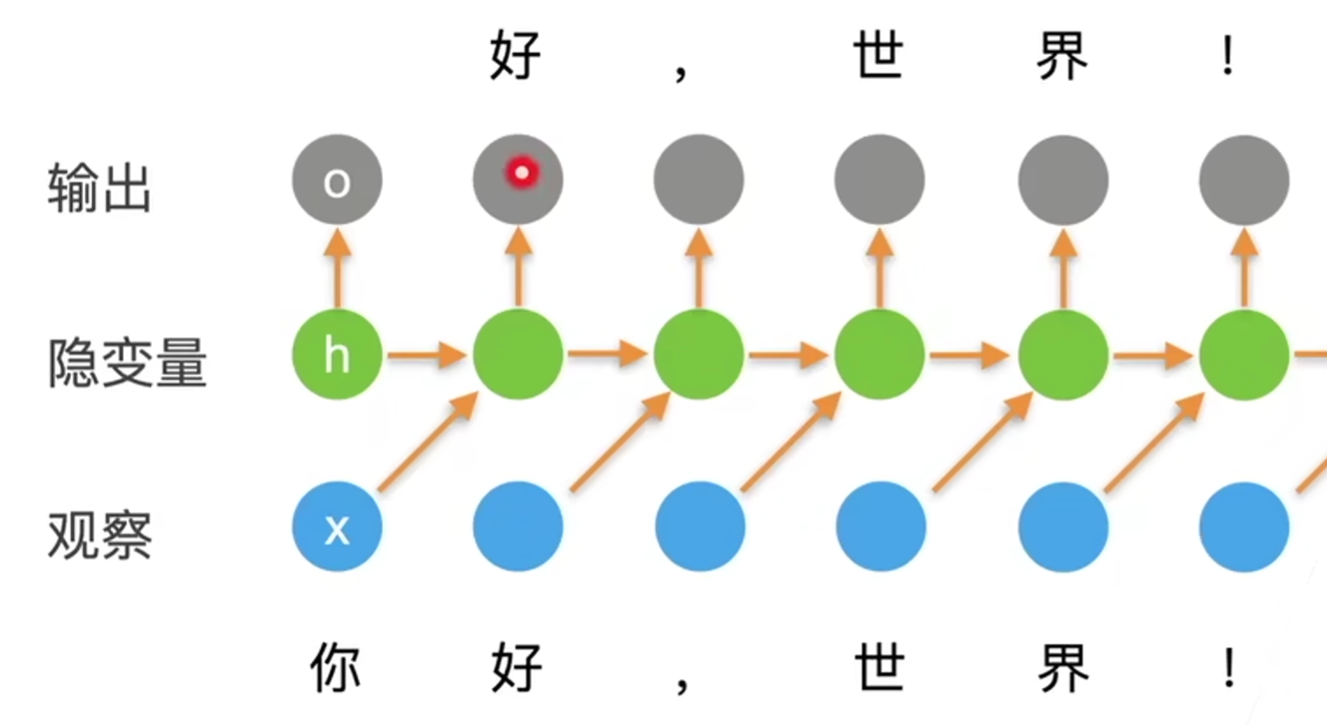
- \(o_t\)是根据\(h_t\)得到的,而\(h_t\)依赖的是\(x_{t-1}\)及之前的输入
- 即输出\(o_t\)之前,不能看到\(x_t\)
- 通过\(o_t\)和\(x_t\)之间的误差,计算损失函数
- RNN是通过\(W_{hh}\)来存储时序信息的(即,隐变量的横向箭头)
困惑度 perplexity
语言模型可以视为一个多分类任务(预测词汇,有len(vocab)个类别)。
衡量一个语言模型的好坏可以用平均交叉熵:
\[\pi = \frac{1}{n} \sum_{i=1}^n\log p(x_t|x_{t-1}, ...)
\]
其中,\(p\)是语言模型的预测模型,\(x_t\)是真实词。
由于历史原因,NLP使用困惑度 \(exp(\pi)\) 来衡量,其中
- 1表示完美
- 无穷大表示最差情况
李普希茨连续 Lipschitz continuous
假设在向量形式的\(\mathbf{x}\)中,使用\(\eta > 0\)作为学习率,我们将\(\mathbf{x}\)更新为\(\mathbf{x}-\eta \mathbf{g}\)。
如果我们进一步假设目标函数\(f\)表现良好,即函数\(f\)在常数\(L\)下是李普希茨连续的:
\[|f(\mathbf{x}) - f(\mathbf{x} - \eta \mathbf{g})| \leq L\eta||\mathbf{g}||
\]
这意味着我们不会观察到超过\(L\eta||\mathbf{g}||\)的变化。这既是坏事也是好事。
- 坏的方面:限制了取得进展的速度。
- 好的方面:限制了事情变遭的程度,尤其当我们朝着错误的方向前进时。
梯度剪裁 gradient clipping
梯度剪裁能够有效防止梯度爆炸。
如果梯度范数超过\(\theta\),则将梯度投影回半径为\(\theta\)的球。
\[\mathbf{g} \leftarrow min(1, \frac{\theta}{||\mathbf{g}||})\mathbf{g}
\]
RNN的Pytorch实现
- Y是每个时间步的隐状态,这些隐状态可以作为后续输出层(Linear)的输入
- state,state_new分别是更新前后的隐状态
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
# 批量大小,时间步长
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# 构造一个具有256个隐藏单元的单隐藏层
num_hiddens = 256
rnn_layer = nn.RNN(len(vocab), num_hiddens)
# 初始化隐状态h
state = torch.zeros((1, batch_size, num_hiddens))
# 形状为(隐藏层数,批量大小,隐藏单元数)
# state.shape
# torch.Size([1, 32, 256])
X = torch.rand(size=(num_steps, batch_size, len(vocab)))
Y, state_new = rnn_layer(X, state)
# Y.shape, state_new.shape
# (torch.Size([35, 32, 256]), torch.Size([1, 32, 256]))
class RNNModel(nn.Module):
"""循环神经网络模型"""
def __init__(self, rnn_layer, vocab_size, **kwargs):
super(RNNModel, self).__init__(**kwargs)
self.rnn = rnn_layer
self.vocab_size = vocab_size
self.num_hiddens = self.rnn.hidden_size
# 如果RNN是双向的(之后将介绍),num_directions应该是2,否则应该是1
if not self.rnn.bidirectional:
self.num_directions = 1
self.linear = nn.Linear(self.num_hiddens, self.vocab_size)
else:
self.num_directions = 2
self.linear = nn.Linear(self.num_hiddens * 2, self.vocab_size)
def forward(self, inputs, state):
X = F.one_hot(inputs.T.long(), self.vocab_size)
X = X.to(torch.float32)
# 隐状态层
Y, state = self.rnn(X, state)
# 全连接层首先将Y的形状改为(时间步数*批量大小,隐藏单元数)
# 它的输出形状是(时间步数*批量大小,词表大小)。
# 输出层
output = self.linear(Y.reshape((-1, Y.shape[-1])))
return output, state
def begin_state(self, device, batch_size=1):
if not isinstance(self.rnn, nn.LSTM):
# nn.GRU以张量作为隐状态
return torch.zeros((self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens),
device=device)
else:
# nn.LSTM以元组作为隐状态
return (torch.zeros((
self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens), device=device),
torch.zeros((
self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens), device=device))


 浙公网安备 33010602011771号
浙公网安备 33010602011771号