算法-动态规划-完全背包

0. 动态规划五部曲：

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

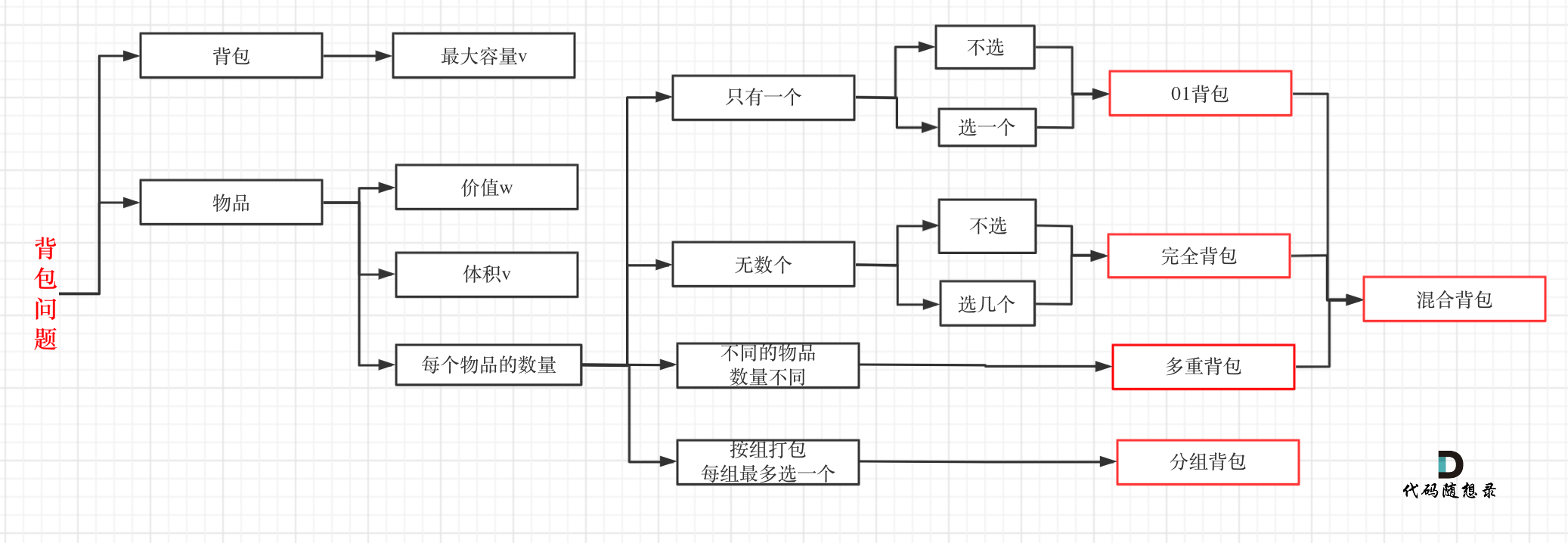
1. 完全背包问题

完全背包问题中，每个物品都有无数个，可以重复选择。

二维dp数组

    int[][] dp = new int[n][totalWeight+1];
    
    // 初始化第一行
    for(int j = weight[0]; j<=totalWeight; ++j) {
        dp[0][j] = value[0] * (j/weight[0]);
    }
    
    for(int i = 1; i<n; ++i) {
        for(int j = 0; j<=totalWeight; ++j) {
            if(j < weight[i])
                dp[i][j] = dp[i-1][j];
            else 
                dp[i][j] = Math.max(dp[i-1][j], dp[i][j-weight[i]]+value[i]);
        }
    }

一维dp数组：顺序遍历，允许同种物品被重复选择。

    int[] dp = new int[totalWeight+1];
    for(int i = 0; i<n; ++i) {
        for(int j = weight[i]; j<=totalWeight; ++j) {
            dp[j] = Math.max(dp[j], dp[j-weight[i]] + value[i]);
        }
    }

import java.util.Scanner;

public class Main{
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int totalWeight = scanner.nextInt();
        int[] weight = new int[n];
        int[] value = new int[n];
        
        for(int i = 0; i<n; ++i) {
            weight[i] = scanner.nextInt();
            value[i] = scanner.nextInt();
        }
        
        int[] dp = new int[totalWeight+1];
        for(int i = 0; i<n; ++i) {
            // 顺序遍历，同一个物品可以重复选
            for(int j = weight[i]; j<=totalWeight; ++j) {
                dp[j] = Math.max(dp[j], dp[j-weight[i]]+value[i]);
            }
        }
        
        System.out.println(dp[totalWeight]);
    }
}

2. 零钱兑换II (LeetCode 518)

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。

注意：

背包问题的递推式会根据题意而变化
完全背包不是仅依赖于左边，可以依赖所有在dp[i][j]之前计算出来的数值

class Solution {
    public int change(int amount, int[] coins) {
        int n = coins.length;
        int[][] dp = new int[n][amount+1];
        // 初始化第一行
        for(int j = coins[0]; j<=amount; ++j) {
            if(j % coins[0] == 0)
                dp[0][j] = 1;
        }

        for(int i = 0; i<n; ++i) {
            dp[i][0] = 1;
        }

        for(int i = 1; i<n; ++i) {
            for(int j = 1; j<=amount; ++j) {
                if(j < coins[i])
                    dp[i][j] = dp[i-1][j];
                else 
                    // 不选/选coins[i]
                    dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]];
            }
        }

        return dp[n-1][amount];
    }
}

3. 组合总和 IV (LeetCode 377)

给你一个由不同整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

注意：

顺序不同的序列被视作不同的组合，即本题求的是排列数
可以看成是爬楼梯，递推公式为if(nums[i] > j) dp[j] += dp[j-nums[i]]

class Solution {
    // 可以看成有n种步长的爬楼梯问题
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target+1];
        dp[0] = 1;
        for(int j = 1; j<=target; ++j) {
            for(int num : nums) {
                if(j >= num) {
                    dp[j] += dp[j-num];
                }
            }
        }

        return dp[target];
    }
}

4. 零钱兑换(LeetCode 322)

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。
计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。
你可以认为每种硬币的数量是无限的。

class Solution {
    public int coinChange(int[] coins, int amount) {
        if(amount == 0) return 0;

        int n = coins.length;
        int[][] dp = new int[n][amount+1];

        for(int i = coins[0]; i<=amount; i+=coins[0]) {
            dp[0][i] = i/coins[0];
        }

        for(int i = 1; i<n; ++i) {
            for(int j = 1; j<=amount; ++j) {
                if(j < coins[i])
                    dp[i][j] = dp[i-1][j];
                else if(j == coins[i])
                    dp[i][j] = 1;
                else 
                    // 先满足能够凑满，再考虑用最少的个数，避免min中取到0（错误地将可实现变为不可实现）
                    if(dp[i][j-coins[i]] == 0)
                        dp[i][j] = dp[i-1][j];
                    else if(dp[i-1][j] == 0) 
                        dp[i][j] = dp[i][j-coins[i]] + 1;
                    else 
                        dp[i][j] = Math.min(dp[i-1][j], dp[i][j-coins[i]] + 1);
            }
        }

        return (dp[n-1][amount] == 0) ? -1 : dp[n-1][amount];
    }
}

5. 完全平方数(LeetCode 279)

给你一个整数 n ，返回和为 n 的完全平方数的最少数量。
完全平方数是一个整数，其值等于另一个整数的平方；

class Solution {
    // 二维dp数组
    public int numSquares(int n) {
        int m = (int) Math.sqrt(n);
        int[][] dp = new int[m+1][n+1];

        for(int j = 0; j<=n; ++j) {
            dp[1][j] = j;
        }

        for(int i = 2; i<=m; ++i) {
            for(int j = 1; j<=n; ++j) {
                if(j < i * i)
                    dp[i][j] = dp[i-1][j];
                else 
                    dp[i][j] = Math.min(dp[i-1][j], dp[i][j-i*i] + 1);
            }
        }

        return dp[m][n];
    }

    // 一维dp数组
    public int numSquares(int n) {
        int m = (int) Math.sqrt(n);
        int[] dp = new int[n+1];

        for(int j = 0; j<=n; ++j) {
            dp[j] = j;
        }

        for(int i = 2; i<=m; ++i) {
            for(int j = i*i; j<=n; ++j) {
                dp[j] = Math.min(dp[j], dp[j-i*i]+1);
            }
        }

        return dp[n];
    }
}

6. 单词拆分(LeetCode 139)

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
     注意，你可以重复使用字典中的单词。

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        int n = wordDict.size();
        int len = s.length();
        // 长度为i的串是否能够拆分维wordDict中的拼接
        boolean[] dp = new boolean[len+1];

        dp[0] = true;

        int wordLen;
        for(int j = 1; j<=len; ++j) {
            for(int i = 0; i<n; ++i) {
                wordLen = wordDict.get(i).length();
                if(j >= wordLen) {
                    dp[j] = (dp[j] || (dp[j-wordLen] && wordDict.get(i).equals(s.substring(j-wordLen, j)))); 
                }
            }
        }

        return dp[len];
    }
}

posted @ 2024-08-29 11:55 Frank23 阅读(54) 评论(0) 收藏举报

刷新页面返回顶部

Keep moving.