相似度调研&&O(1)时间内获得栈或队列最小值
思考题1:调研学习相似度的定义方法。
思考题2: 给出方案实现O(1)时间内获得栈中最小值的函数?假如是队列呢?
思考题1题解:
相似度就是比较两个事物的相似性。查阅现有的方法发现,一般都是通过计算事物的特征之间的距离来度量相似度,如果距离小,那么相似度大;如果距离大,那么相似度小。关于相似度的计算,现有的几种基本方法都是基于向量(Vector)的。
1.Minkowski distance
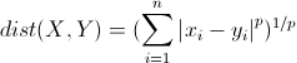
(1)当p=1时,“闵可夫斯基距离”变成“曼哈顿距离”
假设在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离显然不是两点间的直线距离吗,除非能穿越大楼。实际驾驶距离就是“曼哈顿距离”。这也是曼哈顿距离名称的来源, 曼哈顿距离也称为城市街区距离(City Block distance)。
(2)当p=2时,“闵可夫斯基距离”变成“欧几里得距离”
欧氏距离(也称欧几里得度量)指在n维空间中两个点之间的真实距离。
(3)当p=∞时,“闵可夫斯基距离”变成“切比雪夫距离”
二个点之间的切比雪夫距离定义是指各坐标数值差绝对值的最大值。若将国际象棋棋盘放在二维直角坐标系中,格子的边长定义为1,座标的x轴及y轴和棋盘方格平行,原点恰落在某一格的中心点,则王从一个位置走到其他位置需要的步数恰为二个位置的切比雪夫距离,因此切比雪夫距离也称为棋盘距离。
(4)闵氏距离的缺点主要有两点:
①将各个分量的量纲当作相同的看待。
②没有考虑各个分量的分布(期望,方差等)可能是不同的。
2.Hamming distance
两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
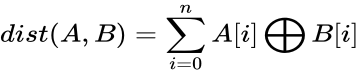
应用:信息编码(为了增强容错性,应使得编码间的最小汉明距离尽可能大)。
3.Cosine Similarity
余弦距离,也称为余弦相似度,是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。
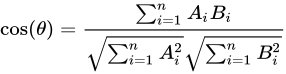
应用:判断两段文本的语义相似度,用余弦值衡量文本相似度。
4.Pearson Correlation Coefficient
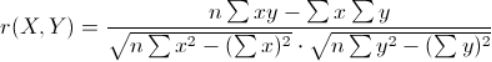
应用:计算相关相似性,通过Peason相关系数来度量两个用户的相似性。计算时,首先找到两个用户共同评分过的项目集,然后计算这两个向量的相关系数。
5.Jaccard Similarity
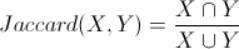
应用:Jaccard系数主要用于计算符号度量或布尔值度量的个体间的相似度,因为特征属性都是由符号度量或者布尔值标识,因此无法衡量差异具体值的大小,只能获得“是否相同”这个结果,所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。
思考题2题解:
1.O(1)时间内获得栈的最小值
①问题分析:
如果只是考虑当前栈的最小值,那么直接添加一个辅助变量Min,在入栈时实时更新Min即可,可以在O(1)时间内获得当前栈的最小值。
这样做的问题在于,如果最小值出栈,那么最小值Min必须要更新,就必须重新遍历栈获得最小值,这样做最坏的情况下是O(n)的时间复杂度。
那么能不能既获得当前栈的最小值,又记录历史栈的最小值?
之前在LeetCode上刷过一道寻找下一个更大元素。
题目用单调栈记录了历史和现在的最值。
本题不过是这道题的简化版。
②求解思路:
借助一个单调不增栈,记录历史和现在的最小值。
如果单调栈为空或者单调栈栈顶元素小于要入栈的元素,则当前元素入数据栈和单调栈,否则,只入单调栈。
③代码
class MinStack{
List<Integer> stack;
List<Integer> minStack;
public MinStack(){
stack = new LinkedList<Integer>();
minStack = new LinkedList<Integer>();;
}
void push(int val){
//如果单调栈为空或者当前入栈元素小于单调栈栈顶元素,则当前入栈元素进单调栈
if(minStack.isEmpty()||val<=minStack.get(minStack.size()-1)){
minStack.add(val);
}
stack.add(val);
}
int pop(){
if(stack.get(stack.size()-1)==minStack.get(minStack.size()-1)) {
//如果当前出栈是最小元素,单调栈出栈
minStack.remove(minStack.size()-1);
}
return stack.remove(stack.size()-1);
}
int getMin(){
return minStack.get(minStack.size()-1);
}
boolean isEmpty(){
return stack.size() == 0;
}
@Override
public String toString() {
StringBuffer sb = new StringBuffer();
sb.append("Stack:{");
for(int i:stack){
sb.append(i+",");
}
sb.deleteCharAt(sb.length()-1);
sb.append("}");
return sb.toString();
}
}
④测试:
测试1最小值唯一:
public class Test {
public static void main(String[] args) {
MinStack stack = new MinStack();
stack.push(2);
stack.push(4);
stack.push(1);
stack.push(9);
stack.push(3);
stack.push(7);
while(!stack.isEmpty()){
System.out.println(stack);
System.out.println("当前最小值为"+stack.getMin());
stack.pop();
}
}
}
输出1:
Stack:{2,4,1,9,3,7}
当前最小值为1
Stack:{2,4,1,9,3}
当前最小值为1
Stack:{2,4,1,9}
当前最小值为1
Stack:{2,4,1}
当前最小值为1
Stack:{2,4}
当前最小值为2
Stack:{2}
当前最小值为2
测试2最小值不唯一:
public class Test {
public static void main(String[] args) {
MinStack stack = new MinStack();
stack.push(7);
stack.push(4);
stack.push(-1);
stack.push(9);
stack.push(-1);
stack.push(0);
while(!stack.isEmpty()){
System.out.println(stack);
System.out.println("当前最小值为"+stack.getMin());
stack.pop();
}
}
}
输出2:
Stack:{7,4,-1,9,-1,0}
当前最小值为-1
Stack:{7,4,-1,9,-1}
当前最小值为-1
Stack:{7,4,-1,9}
当前最小值为-1
Stack:{7,4,-1}
当前最小值为-1
Stack:{7,4}
当前最小值为4
Stack:{7}
当前最小值为7
2.O(1)时间内获得队列的最小值
①解题思路:
与栈相似的思路,只需把单调不增栈改成单调不减双向队列。
若单调队列为空或队尾元素小于等于入队元素,则当前入队元素进数据队列和单调队列;否则,若队尾元素大于入队元素,则单调队列队尾一直出队直到队尾元素小于等于入队元素。
若出队元素等于单调队列队首元素,则单调队列队首元素出队。
获得最小元素,只需要获得单调队列的队首元素。
②代码:
class MinQueue{
List<Integer> queue;
List<Integer> minQueue;
public MinQueue(){
queue = new LinkedList<Integer>();
minQueue = new LinkedList<Integer>();;
}
void append(int val){
if(minQueue.isEmpty()||val>=minQueue.get(minQueue.size()-1)){
//如果单调队列为空或者当前入队列元素大于等于单调队列队尾元素,则当前入队列元素进单调队列
minQueue.add(val);
}else{
while(!minQueue.isEmpty()&&minQueue.get(minQueue.size()-1)>val){
minQueue.remove(minQueue.size()-1);
}
//若队尾元素大于入队元素,则单调队列队尾一直出队直到队尾元素小于等于入队元素或单调队列为空。
minQueue.add(val);
}
queue.add(val);
}
int get(){
if(queue.get(0)==minQueue.get(0)) {
//如果当前出队列是最小元素,单调队列队首元素出队
minQueue.remove(0);
}
return queue.remove(0);
}
int getMin(){
return minQueue.get(0);
}
boolean isEmpty(){
return queue.size() == 0;
}
@Override
public String toString() {
StringBuffer sb = new StringBuffer();
sb.append("Queue:{");
for(int i:queue){
sb.append(i+",");
}
sb.deleteCharAt(sb.length()-1);
sb.append("}");
return sb.toString();
}
}
③测试:
测试1最小值唯一:
public class Test {
public static void main(String[] args) {
MinQueue queue = new MinQueue();
queue.append(1);
queue.append(2);
queue.append(11);
queue.append(0);
queue.append(8);
queue.append(4);
while(!queue.isEmpty()){
System.out.println(queue);
System.out.println("当前最小值为"+queue.getMin());
queue.get();
}
}
}
测试1输出:
Queue:{1,2,11,0,8,4}
当前最小值为0
Queue:{2,11,0,8,4}
当前最小值为0
Queue:{11,0,8,4}
当前最小值为0
Queue:{0,8,4}
当前最小值为0
Queue:{8,4}
当前最小值为4
Queue:{4}
当前最小值为4
测试2最小值不唯一:
public class Test {
public static void main(String[] args) {
MinQueue queue = new MinQueue();
queue.append(1);
queue.append(-2);
queue.append(8);
queue.append(15);
queue.append(-2);
queue.append(3);
while(!queue.isEmpty()){
System.out.println(queue);
System.out.println("当前最小值为"+queue.getMin());
queue.get();
}
}
}
测试2输出:
Queue:{1,-2,8,15,-2,3}
当前最小值为-2
Queue:{-2,8,15,-2,3}
当前最小值为-2
Queue:{8,15,-2,3}
当前最小值为-2
Queue:{15,-2,3}
当前最小值为-2
Queue:{-2,3}
当前最小值为-2
Queue:{3}
当前最小值为3


 浙公网安备 33010602011771号
浙公网安备 33010602011771号