230th Weekly Leetcode Contest

题目二

题目描述

5690. 最接近目标价格的甜点成本  难度：中等-中等

题解

解法一：三进制状态压缩

　　考虑到baseCosts、toppingCosts的长度最多都为10，每一种辅料都有加0、1、2份的选择，因此可以考虑三进制状态压缩求解。类似二进制的状态压缩。

以10种辅料为例。

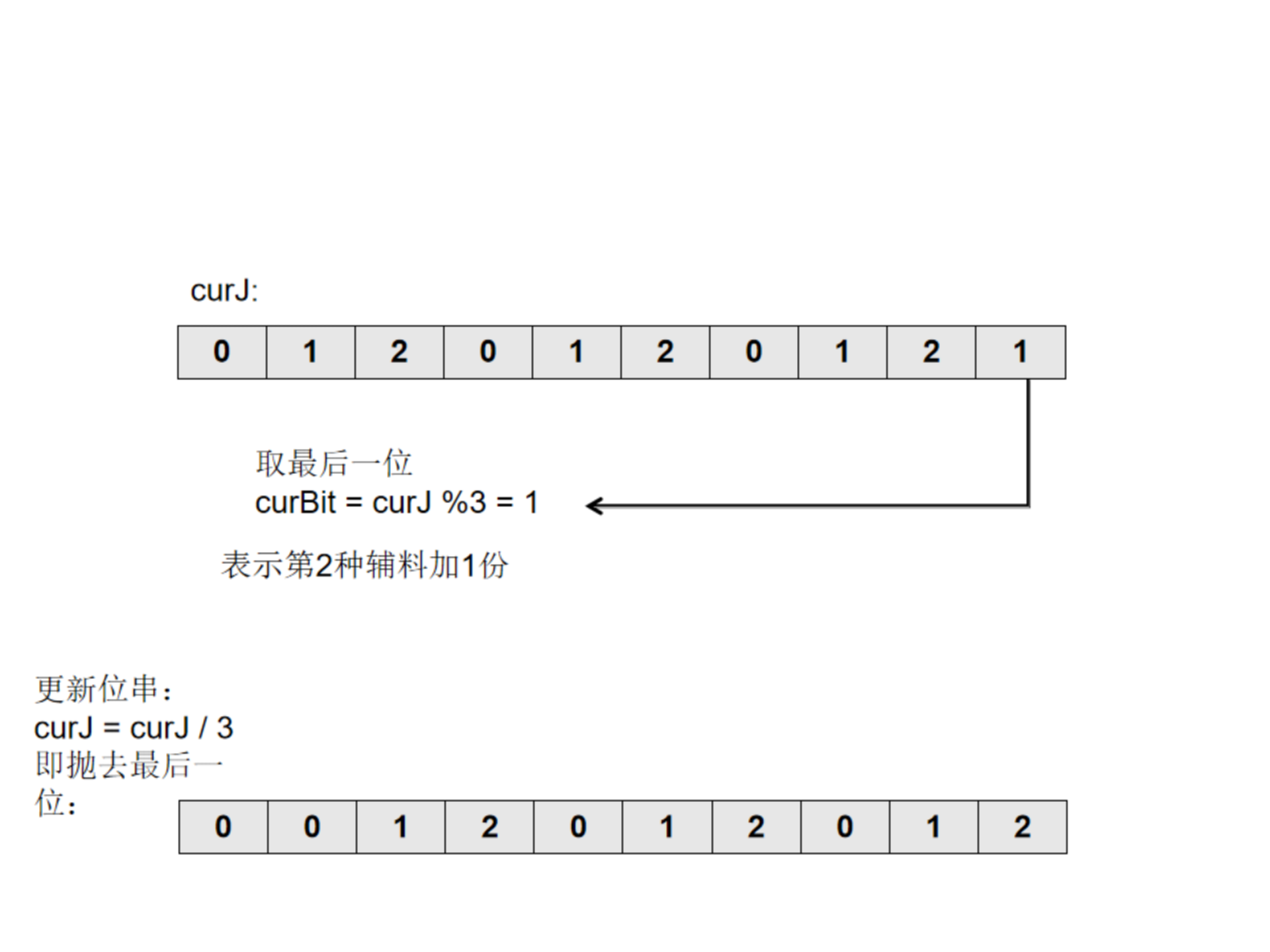
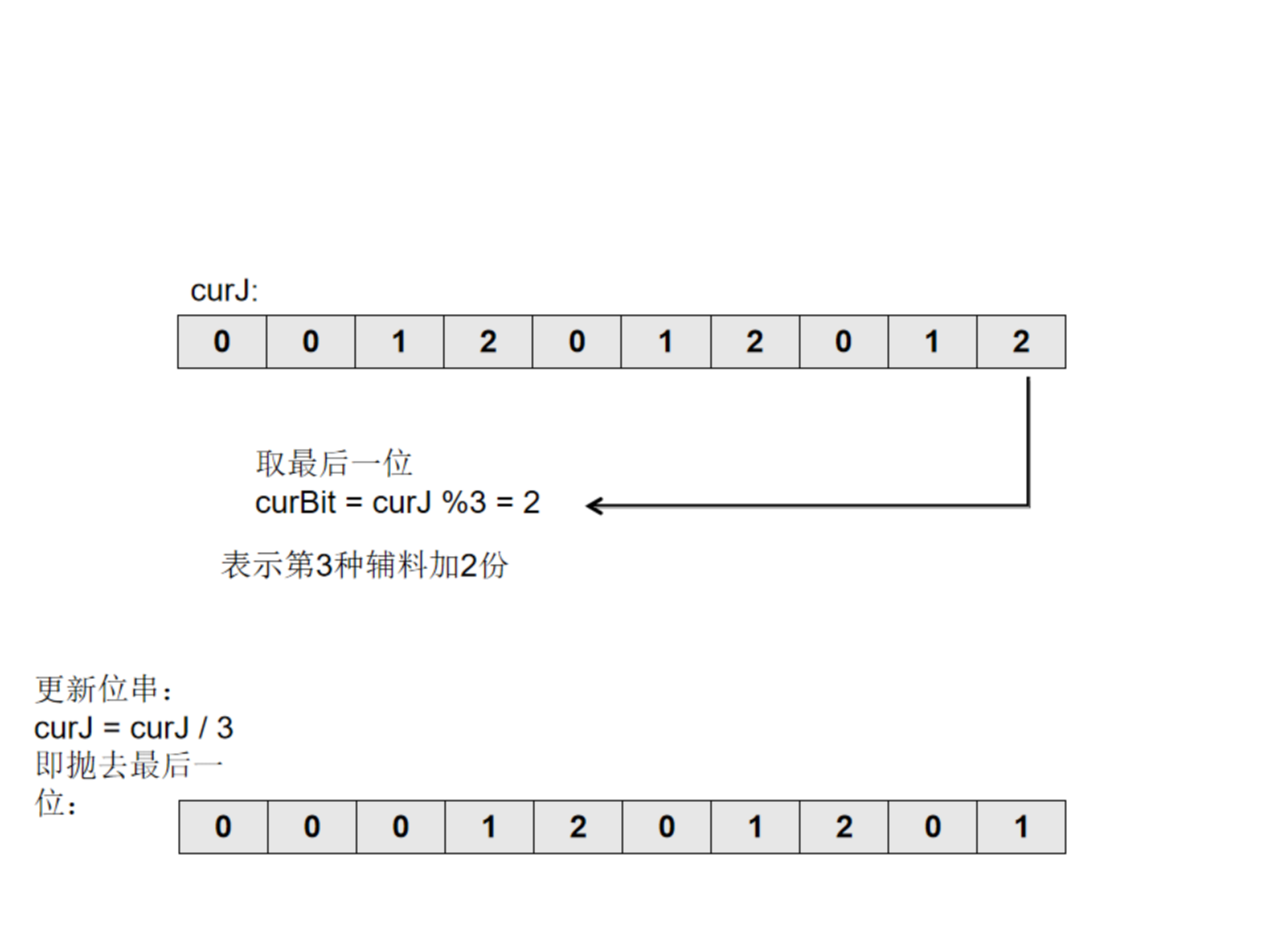
  直到curJ为0。

代码：

class Solution {
    public int closestCost(int[] baseCosts, int[] toppingCosts, int target) {
        Arrays.sort(baseCosts);
        Arrays.sort(toppingCosts);
        int nearestCost=0;//记录最接近的成本
        int minGap = Integer.MAX_VALUE;//记录目前最接近的成本和目标成本target的差
        for(int i=0;i<baseCosts.length;i++){//每一种基料
            for(int j=0;j<Math.pow(3,toppingCosts.length);j++){//三进制位串
                int cost = baseCosts[i];
                int curJ = j;//现在的位串
                int index = 0;
                while(curJ!=0){//取位串的每一位
                    int curBit = curJ % 3;//位串的当前一位
                    curJ /= 3;
                    cost += toppingCosts[index]*curBit;
                    index++;
                }
                if(Math.abs(cost-target)==0){//若现在的成本恰好是target，直接返回
                    return target;
                }else if(Math.abs(cost-target)<minGap){//若目前的成本更接近target，更新nearestCost和minGap;
                    minGap = Math.abs(cost-target);
                    nearestCost = cost;
                }else if(Math.abs(cost-target)==minGap){//若目前的成本和已经找到的最接近成本与目标成本的差距相等，取成本较小者（题目要求）
                    if(cost<nearestCost){
                        nearestCost = cost;
                    }
                }
            }
        }
        return nearestCost;
    }
}

略微优化代码：

　　当目前的cost>target 且 Math.abs(cost-target)>minGap时，由于cost随着位串的遍历单调不减，这种方案可以不再考虑，肯定不优于已经求得的成本，因此可以剪枝。

　　

class Solution {
    public int closestCost(int[] baseCosts, int[] toppingCosts, int target) {
        Arrays.sort(baseCosts);
        Arrays.sort(toppingCosts);
        int nearestCost=Integer.MAX_VALUE;//记录最接近的成本
        int minGap = Integer.MAX_VALUE;//记录目前最接近的成本和目标成本target的差
        for(int i=0;i<baseCosts.length;i++){//每一种基料
            for(int j=0;j<Math.pow(3,toppingCosts.length);j++){//三进制位串
                int cost = baseCosts[i];
                int curJ = j;//现在的位串
                int index = 0;
                boolean isCut = false;
                while(curJ!=0){//取位串的每一位
                    int curBit = curJ % 3;//位串的当前一位
                    curJ /= 3;
                    cost += toppingCosts[index]*curBit;
                    index++;
                    if(cost>target&&Math.abs(cost-target)>minGap){//剪枝
                        isCut = true;
                        break;
                    }
                }
                if(isCut==true){//剪枝
                    continue;
                }
                if(Math.abs(cost-target)==0){//若现在的成本恰好是target，直接返回
                    return target;
                }else if(Math.abs(cost-target)<minGap){//若目前的成本更接近target，更新nearestCost和minGap;
                    minGap = Math.abs(cost-target);
                    nearestCost = cost;
                }else if(Math.abs(cost-target)==minGap){//若目前的成本和已经找到的最接近成本与目标成本的差距相等，取成本较小者（题目要求）
                    if(cost<nearestCost){
                        nearestCost = cost;
                    }
                }
            }
        }
        return nearestCost;
    }
}

解法二：动态规划

本题数据范围很小，暴力枚举辅料组合就可以通过，但时间复杂度为指数级。

把问题转化为背包问题，可以将时间复杂度降低到多项式级别。

• 因为每种辅料最多可以用两次，所以直接把每种辅料变成两个。
• 基料必须且只能选一种，可以首先处理好。

题目三

题目描述

5691. 通过最少操作次数使数组的和相等 难度：中等-中等

题解-贪心法

看到题目后，总结出以下要点：

• 总和大的数组中元素减小等同于总和小的数组中元素增大（这样转化后，我们在求得每个数组的总和后，两个总和不再狭义地代表每个数组的总和）
• 要实现最小操作次数，考虑从最小的元素开始增大，增大到最大，如1直接变成6；或从最大的元素开始减小，减小到最小，如6直接变成1。
• 如何判断是否已经满足条件呢？既然我们是保证每次改变量都是最大，那么，如果这次改变后，最好是两个总和相等，那么功德圆满，即使不相等，但若实现了两个总和的反转（即大小关系反转），那么因为我们是最大的改变量，我们只需在心中将这次的改变量减小一点，如原来是2直接到6，我们可以改变2到5、4等等，肯定能实现两个总和的相等。
• 题目中固定1-6的数据范围，我们可以指定一个大小为6的数组inc[] (为了方便,inc[0]不用),inc[1]代表两个数组中1或6的个数（总和大的数组中的1可以增大到6、总和小的数组中的6可以减小到1），inc[2]代表两个数组中2或5的个数（总和大的数组中的2可以增大到6、总和小的数组中的5可以减小到1）

class Solution {
    public int minOperations(int[] nums1, int[] nums2) {
        if(Math.min(nums1.length,nums2.length)*6<Math.max(nums1.length,nums2.length)*1){
            return -1;
        }
        int nums1Sum = 0;
        int nums2Sum = 0;
        for(int i=0;i<nums1.length;i++){//统计nums1的和
            nums1Sum += nums1[i];
        }
        for(int i=0;i<nums2.length;i++){//统计nums2的和
            nums2Sum += nums2[i];
        }
        if(nums1Sum==nums2Sum){
            return 0;
        }
        int[] inc = new int[6];//统计nums1 和 nums2中可以增大或减小的数的个数，即1 ~ 5的个数；为了方便，数组容量多1，inc[0]不用
        if(nums1Sum<nums2Sum){
            for(int i=0;i<nums1.length;i++){//nums1Sum较小，考虑nums1中可以增大的数
                if(nums1[i]<6){ // 1 ~ 5
                    inc[nums1[i]]++;
                }
            }
            for(int i=0;i<nums2.length;i++){//nums2Sum较大，考虑nums2中可以减小的数
                if(nums2[i]>1){ // 2 ~ 6    nums2减小相当于nums1增大,如6减小到1，同1增加到6t；又如5减小到1同2增加到6
                    inc[7-nums2[i]]++;
                }
            }
            int cnt=0;
            for(int i=1;i<=5;i++){//此后的nums1Sum已经不是真正意义上的nums1的和
                while(inc[i]!=0){
                    nums1Sum += 6 - i;
                    inc[i]--;
                    cnt++;
                    if(nums1Sum>=nums2Sum){
                        return cnt;
                    }
                }
            }
        }else if(nums1Sum>nums2Sum){
            for(int i=0;i<nums2.length;i++){//nums2Sum较小，考虑nums2中可以增大的数
                if(nums2[i]<6){ // 1 ~ 5
                    inc[nums2[i]]++;
                }
            }
            for(int i=0;i<nums1.length;i++){//nums1Sum较大，考虑nums1中可以减小的数
                if(nums1[i]>1){ // 2 ~ 6    nums1减小相当于nums2增大,如6减小到1，同1增加到6；又如5减小到1同2增加到6
                    inc[7-nums1[i]]++;
                }
            }
            int cnt=0;
            for(int i=1;i<=5;i++){
                while(inc[i]!=0){
                    nums2Sum += 6 - i;
                    inc[i]--;
                    cnt++;
                    if(nums2Sum>=nums1Sum){
                        return cnt;
                    }
                }
            }
        }
         return -1;
    }
}

题目三

题目描述

5691. 通过最少操作次数使数组的和相等  难度：困难-简单

题解