向量求导
因变量为标量,自变量为向量
参考
\(y\) 为因变量,标量;\(X=[x_1,x_2,\dots,x_n]^T\) 为自变量是向量,n维。
\(y=f(X)\),即!!\(y = f(x_1,x_2,\dots,x_n)\)
因此可以直接求导:
\[\frac{\partial y}{\partial X} = (\frac{\partial y}{\partial x_1};\frac{\partial y}{\partial x_2};\dots;\frac{\partial y}{\partial x_n})
\]
求导结果为n维向量
以\(y = \vec a ^T\vec x\):表示y为两个向量的内积,结果为一个标量
则求\(\frac{\partial y}{\partial \vec x}\),只需求出所有的\(\frac{\partial y}{\partial \vec x_i}\)即可。
具体方法为:
将\(y\)的表达式展开成累加和的形式,然后套用标量的求导法则即可,这一方法适用于所有多维情况的求导。
解:
\[y = \vec a^T\vec x=\sum_{i=1}^n a_i x_i
\]
故对\(\forall i\):
\[\frac{\partial y}{\partial x_i} = a_i
\]
故:
\[\begin{aligned}
\frac{\partial y}{\partial \vec x}&=(\frac{\partial y}{\partial x_1};\frac{\partial y}{\partial x_2};\dots;\frac{\partial y}{\partial x_n}) \\
~&=(a_1;a_2;\dots ;a_n) \\
~&=a
\end{aligned}
\]
注意:若\(y=\vec x 点乘 \vec x\), 则求导结果是\(2\vec x\)
例子:
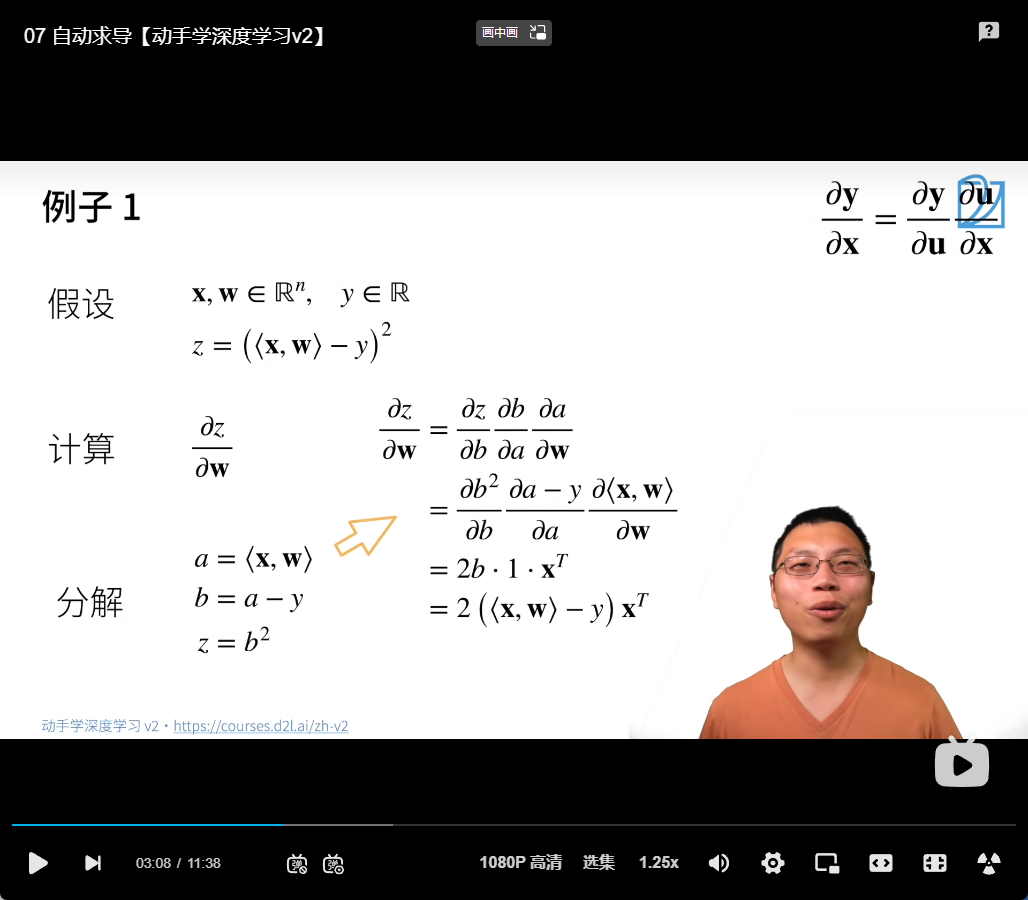
注意图中,向量\(x\)与\(w\)均写成了1n的形式,而不是我们通常的n1,因此最终算出来的结果里面为\(x^T\),而不是\(x\)
因变量、自变量均为向量
当自变量和因变量均为向量时,求导结果为一个矩阵,我们称该矩阵为雅可比矩阵(Jacobian Matrix)。
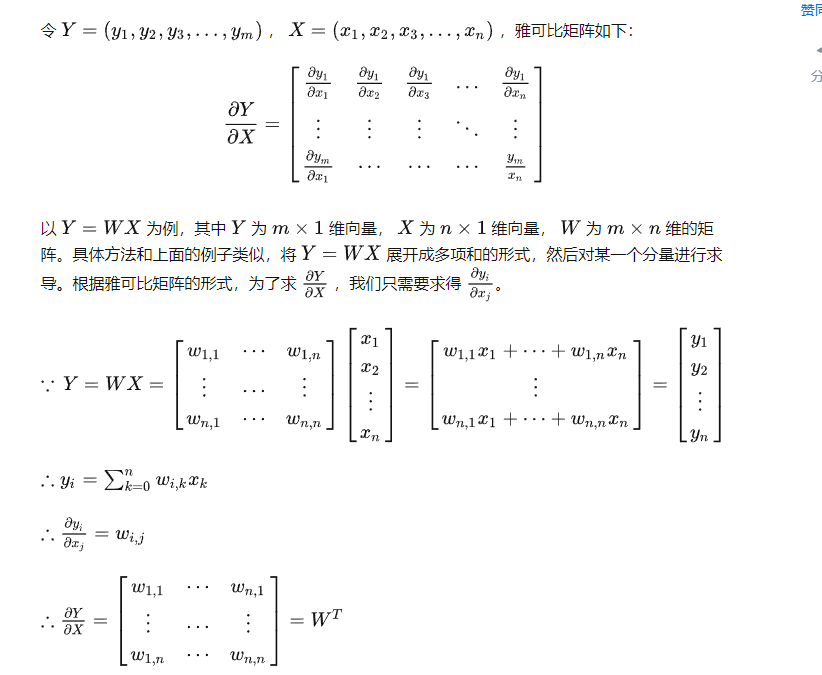
特别的,如果X为n*m的矩阵,w为m维向量,则
\[\frac{\partial X}{\partial \vec w} = X
\]
证明:
设
\[X = \begin{bmatrix}
x_{11}&x_{12}&\dots&x_{1m}\\
x_{21}&x_{22}&\dots&x_{2m}\\
\vdots&\vdots&\ddots&\vdots\\
x_{n1}&x_{n2}&\dots&x_{nm}
\end{bmatrix},
w = \begin{bmatrix}
w_{1}\\
w_2\\
\vdots\\
w_m
\end{bmatrix}
\]
则,
\[\vec z=Xw=\begin{bmatrix}
x_{11}w_1+x_{12}w_2+\dots+x_{1m}w_m\\
x_{21}w_1+x_{22}w_2+\dots+x_{2m}w_m\\
\vdots\\
x_{n1}w_1+x_{n2}w_2+\dots+x_{nm}w_m
\end{bmatrix}=\begin{bmatrix}
z_1\\
z_2\\
\vdots\\
z_n
\end{bmatrix}
\]
则
\[\begin{aligned}
\frac{\partial X\vec w}{\partial \vec w} &= \frac{\partial \vec z}{\partial \vec w}\\
&=\begin{bmatrix}
\frac{\partial z_1}{\partial w_1}&\frac{\partial z_1}{\partial w_2}&\dots&\frac{\partial z_1}{\partial w_m}\\
\frac{\partial z_2}{\partial w_1}&\frac{\partial z_2}{\partial w_2}&\dots&\frac{\partial z_2}{\partial w_m}\\
\vdots&\vdots&\ddots&\vdots\\
\frac{\partial z_n}{\partial w_1}&\frac{\partial z_n}{\partial w_2}&\dots&\frac{\partial z_n}{\partial w_m}\\
\end{bmatrix}\\
&=\begin{bmatrix}
x_{11}&x_{12}&\dots&x_{1m}\\
x_{21}&x_{22}&\dots&x_{2m}\\
\vdots&\vdots&\ddots&\vdots\\
x_{n1}&x_{n2}&\dots&x_{nm}
\end{bmatrix}\\
&=X
\end{aligned}
\]
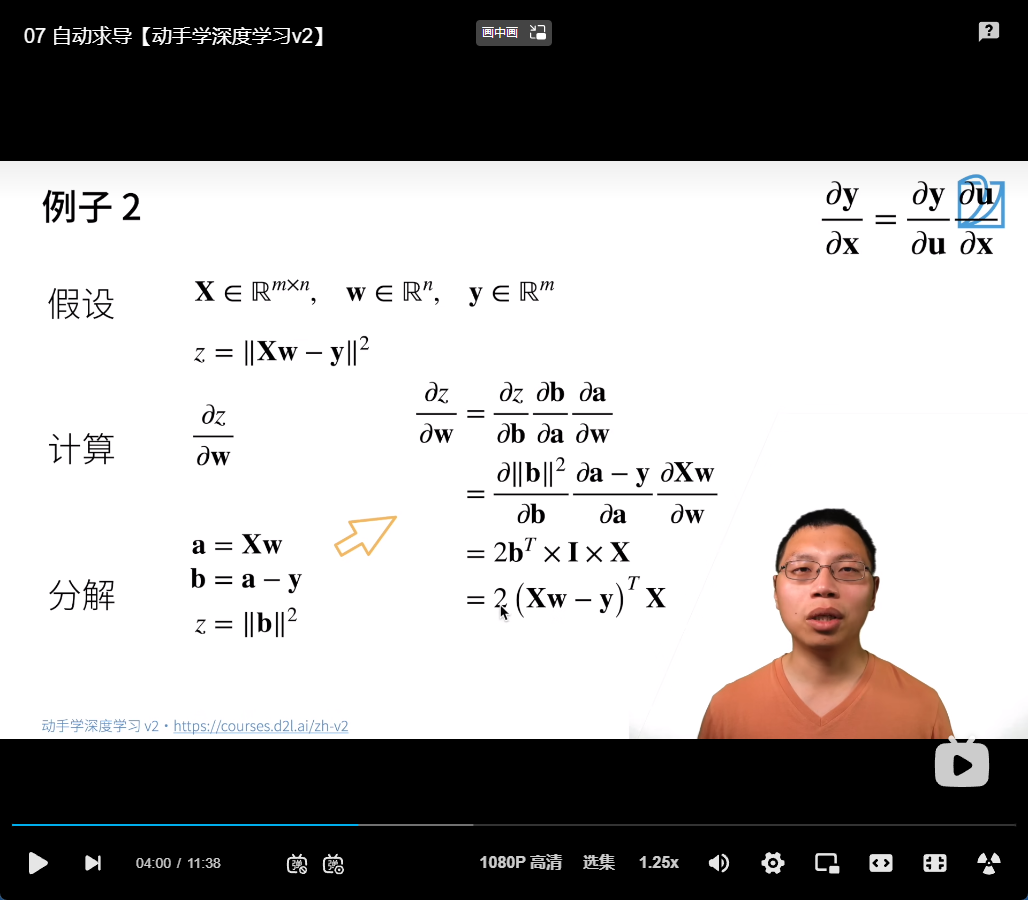
例子:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号