最小生成树(prime+kruskal)
1.prime算法
prime算法类似于bfs,就是判断每次连接的点中距离最短的,加入到树中,具体如下:
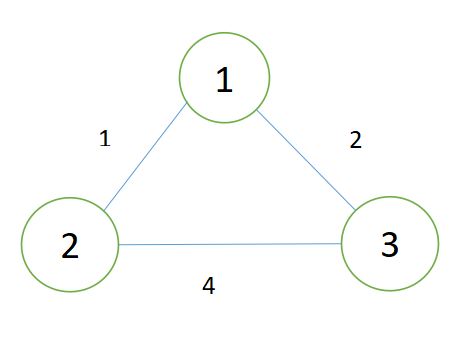
prime算法要求一开始随便选择一个点作为起点,因为最小生成树包括所有点,所以起点随机即可(一般选1),将该点加入一个集合,然后判断集合中所有点与之相连的点中最小的,将其加入集合中,加入集合的点都要用一个vis数组判断是否重复出现过,如果重复出现,就说明你要连接的这两个点已经是连通的了,不需要再直接连接。
比如: 图中三条边,分别为1,2,3,从1开始,1的连接的边两条<1,3>,<1,2>,很明显后者小,所以将后者放入集合,直接在以2为起点时候,判断2是否走过,没走过就说明可以加入树中,然后加入的是<1,3>判断3是否走过,没有加入树,然后就是<2,3>,这里不用纠结<2,3>还是<3,2>,无向图,存边存了两遍,正反各一遍,然后发现3走过,不能加入树,结束,最小生成树的大小是3。
2.kruskal算法
kruskal算法是并查集和贪心的应用,开始时将所有路径的起点,终点,权值加入到一个集合中,然后将集合排序,从小到大以此选择边加入树,为了保证最优,每次要判断加入的边的两端端点是否是相连的( 就是判断两个端点的最顶层父节点是否相同 ),如果不同,则加入树中。
模板
priority_queue<pll,vector<pll>,greater<pll> > q;
ll prime(){//prime算法,用链式前向星储存,堆优化
ll ans=0; memset(dis,0x3f,sizeof(dis)); dis[1]=0; memset(vis,0,sizeof(vis)); q.push(make_pair(0,1)); while(!q.empty()&&sum<n){ int u=q.top().first; int v=q.top().second; q.pop(); if(vis[v]) continue; sum++; ans+=u; vis[v]=1; for(int i=head[v];i;i=e[i].next) if(e[i].w<dis[e[i].to]) dis[e[i].to]=e[i].w,q.push(make_pair(dis[e[i].to],e[i].to)); } return ans;
ll kru(){//kruskal模板 int ans=0; sort(a+1,a+1+n*(n-1)/2,cmp); for(int i=1;i<=n*(n-1)/2;i++){ ll px=find(a[i].x);ll py=find(a[i].y); if(px!=py){ pre[px]=py; if(a[i].w>0) ans+=a[i].w; sum++; } if(sum==m-1) return ans; } return ans; }
例题:畅通工程(模板题)
链接:Problem - 1863 (hdu.edu.cn)
题意:找出最小生成树,如过不能构成,就输出'?'。
代码: //kruskal写法
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=1e5+5; struct ss{ ll x,y,w; }a[N]; ll pre[N]; ll n,m; ll find(ll x){ if(pre[x]==x) return x; return pre[x]=find(pre[x]); } bool cmp(ss a,ss b){ return a.w<b.w; } ll cnt; ll kru(){ int ans=0; for(int i=1;i<=m;i++) pre[i]=i; sort(a+1,a+1+n,cmp); for(int i=1;i<=n;i++){ ll px=find(a[i].x);ll py=find(a[i].y); if(px!=py){ pre[px]=py; if(a[i].w>0) ans+=a[i].w; cnt++; } if(cnt==m-1) return ans; } return -1; } signed main(){ while(cin>>n>>m&&n){ for(int i=1;i<=n;i++){ cin>>a[i].x>>a[i].y>>a[i].w; } cnt=0; ll t=kru(); if(t==-1) cout<<"?"<<endl; else cout<<t<<endl; } }
prime 写法
#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<ll,ll> pll; const int N=1e5+5; struct ss{ ll to,w,next; }e[N]; ll pre[N]; ll n,m; ll cnt;ll head[N]; ll dis[N],vis[N]; void add(ll x,ll y,ll w){ e[++cnt].to=y; e[cnt].w=w; e[cnt].next=head[x]; head[x]=cnt; } priority_queue<pll,vector<pll>,greater<pll> > q; ll sum; ll prime(){ ll ans=0; memset(dis,0x3f,sizeof(dis)); dis[1]=0; memset(vis,0,sizeof(vis)); q.push(make_pair(0,1)); while(!q.empty()&&sum<n){ int u=q.top().first; int v=q.top().second; q.pop(); if(vis[v]) continue; sum++; ans+=u; vis[v]=1; for(int i=head[v];i;i=e[i].next) if(e[i].w<dis[e[i].to]) dis[e[i].to]=e[i].w,q.push(make_pair(dis[e[i].to],e[i].to)); } return ans; } signed main(){ while(cin>>n>>m&&n){ cnt=0; memset(head,0,sizeof(head)); for(int i=1;i<=n;i++){ ll x,y,w;cin>>x>>y>>w; add(x,y,w);add(y,x,w); } sum=0; ll t=prime(); if(sum==m) cout<<t<<endl; else cout<<"?"<<endl; } }
例题:继续畅通工程
链接:Problem - 1879 (hdu.edu.cn)
题意:开始已经建造了一些路径,找最小生成树
思路:kruskal就是输入的时候将已经存在的边直接放到并查集中,链接他们的父节点,让他们相通。
prime就是输入的时候将存在的边的权值按0输入即可。
代码:prime算法
#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<ll,ll> pll; const int N=1e5+5; struct ss{ ll to,w,next; }e[N]; ll pre[N]; ll n,m; ll cnt;ll head[N]; ll dis[N],vis[N]; void add(ll x,ll y,ll w){ e[++cnt].to=y; e[cnt].w=w; e[cnt].next=head[x]; head[x]=cnt; } priority_queue<pll,vector<pll>,greater<pll> > q; ll sum; ll prime(){ ll ans=0; memset(dis,0x3f,sizeof(dis)); dis[1]=0; memset(vis,0,sizeof(vis)); q.push(make_pair(0,1)); while(!q.empty()&&sum<n){ int u=q.top().first; int v=q.top().second; q.pop(); if(vis[v]) continue; sum++; ans+=u; vis[v]=1; for(int i=head[v];i;i=e[i].next) if(e[i].w<dis[e[i].to]) dis[e[i].to]=e[i].w,q.push(make_pair(dis[e[i].to],e[i].to)); } return ans; } signed main(){ ios::sync_with_stdio(false); cin.tie(0); while(cin>>n&&n){ cnt=0; memset(head,0,sizeof(head)); for(int i=1;i<=n*(n-1)/2;i++){ ll x,y,w,p;cin>>x>>y>>w>>p; if(p==1) { add(x,y,0),add(y,x,0); } else add(x,y,w),add(y,x,w); } sum=0; cout<<prime()<<endl; } }
kruskal算法
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=1e5+5; struct ss{ ll x,y,w; }a[N]; ll pre[N]; ll n,m; ll find(ll x){ if(pre[x]==x) return x; return pre[x]=find(pre[x]); } bool cmp(ss a,ss b){ return a.w<b.w; } ll cnt,sum; ll kru(){ int ans=0; sort(a+1,a+1+n*(n-1)/2,cmp); for(int i=1;i<=n*(n-1)/2;i++){ ll px=find(a[i].x);ll py=find(a[i].y); if(px!=py){ pre[px]=py; if(a[i].w>0) ans+=a[i].w; sum++; } if(sum==m-1) return ans; } return ans; } signed main(){ while(cin>>n&&n){ for(int i=1;i<=n;i++) pre[i]=i; cnt=0; for(int i=1;i<=n*(n-1)/2;i++){ ll x,y,w,p;cin>>x>>y>>w>>p; if(p==1){ ll px=find(x);ll py=find(y); pre[px]=py; } else a[++cnt].x=x,a[cnt].y=y,a[cnt].w=w; } sum=0; cout<<kru()<<endl; } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号