【最短路】 八数码

传送门

题意

在一个 \(3\times 3\) 的网格中有一个空格其余是 \(1\sim 8\) 的数字不重不漏，每一次操作可以将空格和上下左右进行交换（如果存在）
使之最后变为

过程如下

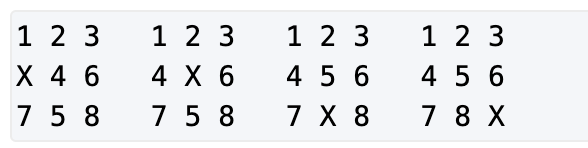
求出最小的交换步骤

数据范围

\(|g| =3\times 3\)

题解

将所有的状态看作图中的一个节点，如果某一个状态通过变换后能变成另一个状态，两个节点之间就连接一条边，bfs 求最短路
每个状态都是 \(3\times 3\) 的矩阵，

• 用字符串表示状态, 存入队列
• 如何记录每一个状态的距离，dist 用 hash
• 每次移动都是还原在矩阵中的坐标表然后再压缩回来

Code

#include<bits/stdc++.h> 
using namespace std;

unordered_map<string, int>dist;
string start;

int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};

int bfs(string start) {      
   queue <string> q;
   string end = "12345678x";
   q.push(start);
   dist[start] = 0;

   while(q.size()) {
      auto t = q.front();
      q.pop();

      int d = dist[t];
      if(t == end) return d;

      int k = t.find('x');
      int x = k / 3, y = k % 3;
      for(int i = 0; i < 4; i ++) { // 上下左右交换
         int tx = x + dx[i], ty = y + dy[i];
         if(tx >= 0 && tx < 3 && ty >= 0 && ty < 3) {
            swap(t[k], t[tx * 3 + ty]);
            if(!dist[t]) {
               dist[t] = d + 1;
               q.push(t);
            }
            swap(t[k], t[tx * 3 + ty]); // 换回来
         }
      }
   }
   return -1;
}

int main() {
   for(int i = 0; i < 9 ; ++i) {
      char c; cin>>c;
      getchar();
      start += c;
   }
   cout<<bfs(start);
}