分布函数

1 正态分布

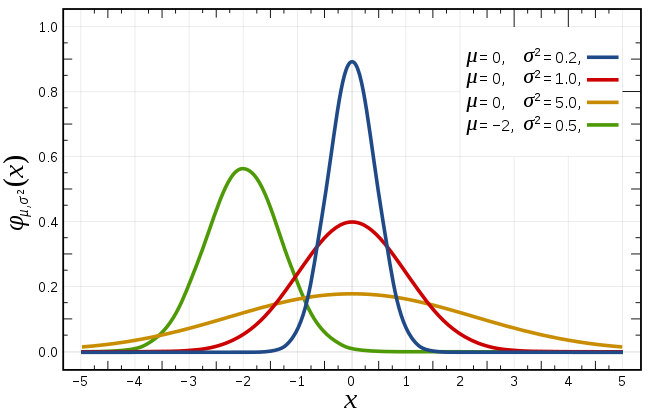
• 又叫高斯分布，一个常见的连续概率密度函数，用于表示一个不明的随机变量，若随机变量\(X\)服从一个位置参数为\(\mu\)，尺度参数为\(\sigma\)的参数
• 记为\(X \sim N\left(\mu, \sigma^{2}\right)\)，

1）概率密度函数

\[f(x ; \mu, \sigma)=\frac{1}{\sigma \sqrt{2 \pi}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) \]

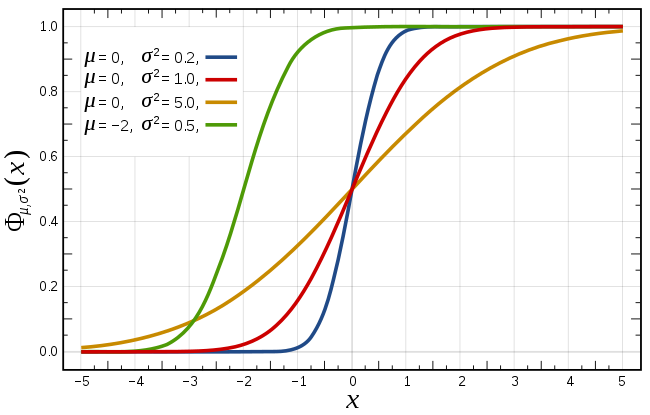
2）累积分布函数

\[F(x ; \mu, \sigma)=\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{x} \exp \left(-\frac{(t-\mu)^{2}}{2 \sigma^{2}}\right) d t \]

3）正态分布的一些性质

• 通常样本分布的均值是近似正态的，即使样本的总体不服从正态分布
• 正态分布的信息熵在所有已知均值和方差的分布中最大，这使得它作为一种均值以及方差已知的分布的自然选择
• 如果\(X \sim N\left(\mu, \sigma^{2}\right)\)，\(a,b\)为实数，那么\(a X+b \sim N\left(a \mu+b,(a \sigma)^{2}\right)\)
• 如果\(X \sim N\left(\mu_{X}, \sigma_{X}^{2}\right)\)与\(Y \sim N\left(\mu_{Y}, \sigma_{Y}^{2}\right)\)是相互独立的统计量
  • 二者的和也满足正态分布\(U=X+Y \sim N\left(\mu_{X}+\mu_{Y}, \sigma_{X}^{2}+\sigma_{Y}^{2}\right)\)
  • 二者的差也满足正态分布\(V=X-Y \sim N\left(\mu_{X}-\mu_{Y}, \sigma_{X}^{2}+\sigma_{Y}^{2}\right)\)
  • 若\(X、Y\)的方差相等，那么\(U、V\)二者是相互独立的

4）中心极限定理

\[定理：在特定条件下，大量统计独立的随机变量的平均值的分布趋近于正态分布 \]

• 根据中心极限定理，当随机变量足够大的时候可以用正态分布来做其他分布的近似
• 参数为\(n\)和\(p\)的二项分布，在\(n\)相当大且\(p\)接近\(0.5\)的时候近似于正态分布
  • 正态分布平均值\(\mu=np\)，方差为\(\sigma^{2}=n p(1-p)\)
• 泊松分布带有参数\(\lambda\)，当样本数量很大的时候近似于正态分布
  • 正态分布的平均值\(\mu=\lambda\)，方差为\(\sigma^{2} = \lambda\)

2 均匀分布

如果连续性变量\(X\)服从一下的概率密度函数，则称\(X\)服从\([a,b]\)上的均匀分布，记做\(X \sim U[a, b]\)

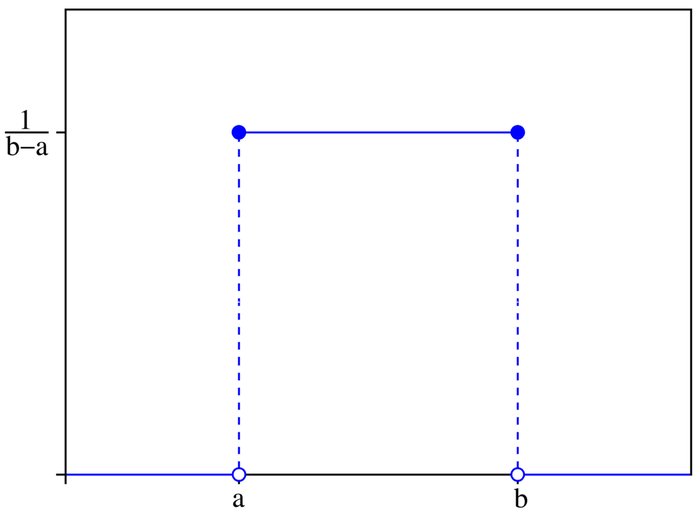
1）概率密度函数

\[f(x)=\left\{\begin{array}{cc}\frac{1}{b-a} & \text { for } a \leq x \leq b \\ 0 & \text { elsewhere }\end{array}\right. \]

2）累积分布函数

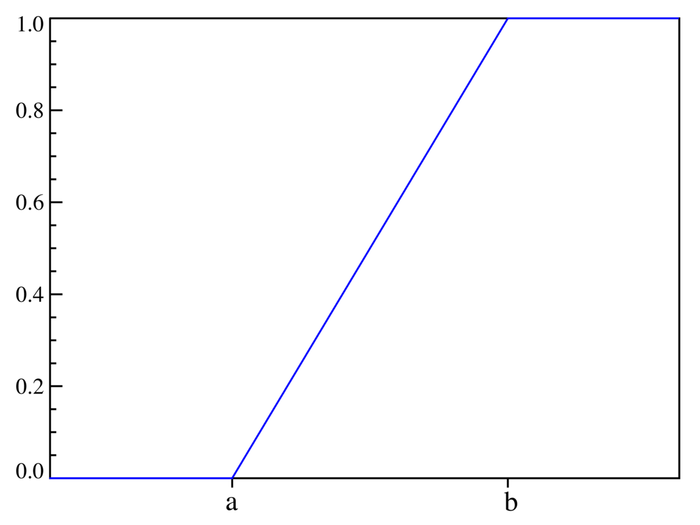
3）期望值和中值

\[E[X]=\frac{(a+b)}{2} \]

4）方差

\[VAR[X]=\frac{(b-a)^{2}}{12} \]

5）子区间概率计算

• 均匀分布具有下属意义的等可能性。
• 若\(X\sim U[a,b]\)，则\(X\)落在\([a,b]\)区间内任意一个子区间\([c,d]\)上的概率为

\[P(c \leq x \leq d)=F(d)-F(c)=\int_{c}^{d} \frac{1}{b-a} d x=\frac{d-c}{b-a} \]

• 概率只与区间的长度有关，与区间的位置无关

3 泊松分布

• 主要用来描述单位时间内随机事件发生的次数的概率分布
• \(X\)服从泊松分布记为\(X \sim \pi(\lambda)\)或\(X \sim P(\lambda)\)

1）概率质量函数（离散的概率密度）

\[P(X=k)=\frac{e^{-\lambda} \lambda^{k}}{k !} \]

2）累积分布函数

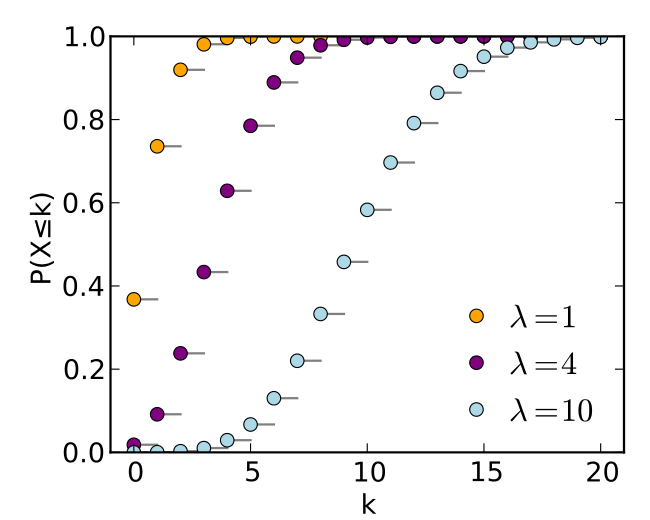
3）方差与期望

• 皆为参数\(\lambda\)

4）泊松过程

泊松过程是随机过程的一种，是以事件的发生事件为定义的
如果一个随机过程\(N(t)\)是一个时间齐次的一维泊松过程，那么它满足以下两个条件

• 在两个互斥（不重叠）的区间内所发生的时间数目是互相独立的随机变量
• 在区间\([t, t+\tau]\)内发生时间的数目的概率分布为

\[P[(N(t+\tau)-N(t))=k]=\frac{e^{-\lambda \tau}(\lambda \tau)^{k}}{k !} \quad k=0,1, \ldots \]

• 其中\(\lambda\)是一个正数，是固定的参数，通常称为抵达率或强度，如果给定时间区间\([t, t+\tau]\)，则事件发生的数目的随机变量\(N(t+\tau)-N(t)\)呈现泊松分布，其参数为\(\lambda \tau\)
• 一个泊松过程的总时间区间内任意两个互斥的子区间满足以下性质
  • 发生的事件数是相互独立的
  • 每一个区间发生的事件数都服从泊松分布

4 指数分布

用来描述独立事件发生的时间间隔，例如旅客进入机场的时间间隔，打进客服中心电话的时间间隔

1）概率密度函数

\[f(x ; \lambda)=\left\{\begin{array}{cc}\lambda e^{-\lambda x} & , x \geq 0 \\ 0 & , x<0\end{array}\right. \]

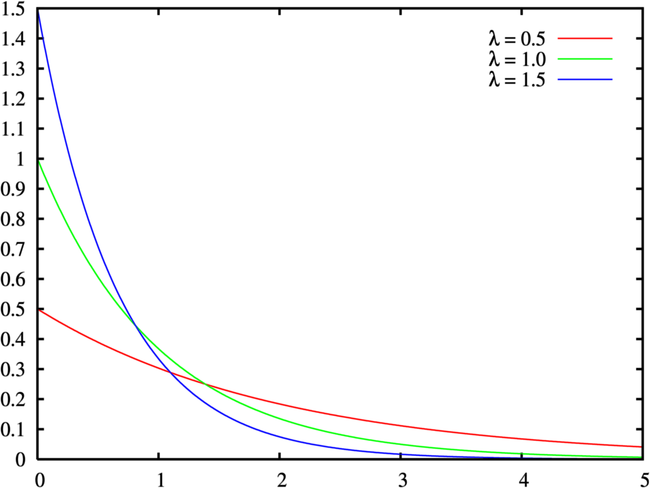
• 其中\(\lambda > 0\)是分布的一个参数，称作率参数，即单位时间发生此事件次数，指数分布的区间为\([0, \infty)\)

2）累计分布函数

\[F(x ; \lambda)=\left\{\begin{array}{cc}1-e^{-\lambda x} & , x \geq 0 \\ 0 & , x<0\end{array}\right. \]

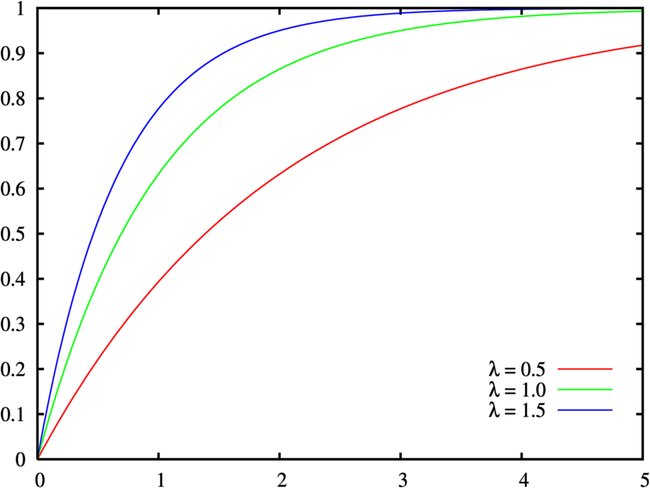
3）期望与方差

• 期望值为：\(\mathbf{E}[X]=\frac{1}{\lambda}\)
  • 比如每个小时接到2个电话，那么接到电话的期望时间就是半个小时
• 方差为：\(\mathbf{D}[X]=\frac{1}{\lambda^{2}}\)

4）无记忆性

• 无记忆性表明如果一个随机变量呈现指数分布，那么它的条件概率服从
  • \(P(T>s+t \mid T>t)=P(T>s) \text { for all } s, t \geq 0\)