插值与拟合

1. 拟合

1.1 线性拟合

1.1.1 多项式拟合

• 采用最小二乘法对于给定的离散或连续的数据求近似函数
• polyfit(x,y,n) ，求出自变量x、因变量y，最高次为n的拟合多项式
• [p,E] = polyfit(x,y,n) ，返回同上的多项式p和矩阵E，矩阵E用于在polyval中计算误差
• ployval(fun , x) ,求变量x在得到的拟合函数处的值
• sym2poly(f),将给定的多项式表示转化从高阶到低阶的系数
• poly2sym([系数]，p),将给定的多项式系数和最高阶转化为多项式
• 拟合的最大阶为length(x)-1

clear;
clc;
digits(5);%设置精度
x=[0.3  0.4  0.7  0.9  1.2  1.9  2.8  3.2  3.7  4.5];
y=[1  2  3  4  5  2  6  9  2  7];

res5 = polyfit(x,y,5); %求得给定自变量为x，因变量为y 的数据，最高阶项为5 的拟合值
% res 中存的是多项式次数从高到低的系数
y_res5 = polyval(res5,x); %得到x在拟合函数处的取值
a5 = vpa(poly2sym(res5),5); %vpa 将系数的精度定位给定的值

res9 = polyfit(x,y,9); 
y_res9 = polyval(res9,x); 
a9 = vpa(poly2sym(res9),9); 
figure;
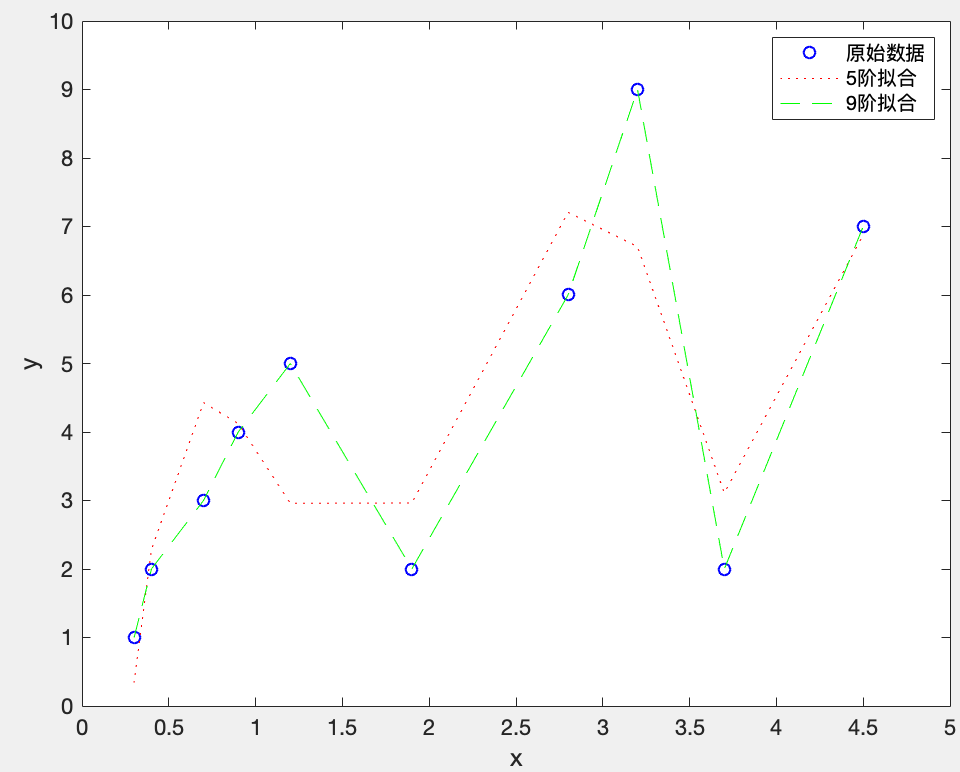
plot(x,y,'bo'); %原始数据，每个点上用空心圆标注
hold on;
plot(x,y_res5,'r:');
plot(x,y_res9,'g--');
axis( [0,5,0,10] ); %设置坐标轴范围[x_st,x_ed,y_st,y_ed]
legend('原始数据','5阶拟合','9阶拟合')
xlabel('x');
ylabel('y');

1.1.2 加权最小方差拟合

1.2 非线性曲线拟合

• 适用于知道输入向量 xdata、输出向量 ydata，并知道输入与输出的函数关系为 ydata=F(x,xdata)，但不清楚系数向量X
• 拟合的目标函数为
• x = lsqcurvefit(fun , x0 , xdata , ydata , opitons)
  • x0为初始解向量，xdata、ydata为满足关系ydata = fun(x , xdata)的数据, options处指明优化参数
  • fun(x , xdata) 为自定义的m文件，用来表示函数关系
• x = lsqcurvefit(fun , x0 , xdata , ydata , lb , ub , opitons)
  • 其中lb为下界，ub为上界，即\(ub \leq x\leq lb\)
• [x , resnorm] = lsqcurvefit(···)
  • resnorm 指的是在每一个x处的平方残差
• [x , resnorm , residual] = lsqcurvefit(···)
  • residual 为每一处x 的残差
• [x , resnorm , residual , exitflag] = lsqcurvefit(···)
  • exitflag 为终止迭代的条件
• [x , resnorm , residual , exitflag , output] = lsqcurvefit(···)
  • output为输出的优化信息

已知输入向量xdata和输出向量ydata，且长度都是n，使用最小二乘非线性拟合函数
\(ydata(i) = x(1) · xdata(i)^{2} + x(2) · sin( xdata( i ) ) +x(3) · xdata(i)^{3}\)

• 定义函数

function f = function_of_min(x,xdata)
    %xdata 是系数
    f = x(1) *xdata.^2 + x(2) * sin(xdata) + x(3) *xdata.^3;
end

• 调用库函数求解

clc,clear,close all;

xdata = [3.6 7.7 9.3 4.1 8.6 2.8 1.3 7.9 10.0 5.4];
ydata = [16.5 150.6 263.1 24.7 208.5 9.9 2.7 163.9 325.0 54.3];

x0=[10,10,10];
[x,resnorm] = lsqcurvefit(@function_of_min,x0,xdata,ydata)

1.3 拟合优度

• 拟合优度(可决系数)：\(R^{2}\)
• 总体平方和\(SST\)：\(S S T=\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}\)
• 误差平方和\(SSE\)：\(S S E=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}\)
• 回归平方和\(SSR\)：\(S S R=\sum_{i=1}^{n}\left(\hat{y}_{i}-\bar{y}\right)^{2}\)
• 可以证明： \(S S T=S S E+S S R\)
• 拟合优度：\(0 \leq R^{2}=\frac{S S R}{S S T}=\frac{S S T-S S E}{S S T}=1-\frac{S S E}{S S T} \leq 1\)
  • \(R^{2}\)越接近1，说明误差平方和越接近0，误差越小说明拟合的越好

2. 插值

• Runge现象
  • 通常使用多项式作为插值的结果函数，认为阶越高拟合程度越高
  • 当阶数>7时，结果函数的振荡程度极高
• 解决方式
  • 避免使用高阶多项式作为插值函数
  • 分段使用低阶多项式作为插值函数整体逼近性更好

2.1 数据网格化

2.2 一维插值

• 即对于函数\(y=f(x)\)进行插值
• yi=interp1(x , y , xi) 返回插值因变量向量\(yi\)
• \(nearest\)，临近点插值
  • yi=interp1(x , y , xi , 'nearest')
• \(linear\)，线性插值
  • yi=interp1(x , y , xi , 'linear') 直线连接相邻点
• \(spline\)，三次样条插值
  • yi=interp1(x , y , xi , 'spline')
• \(pchip\)，分段三次\(Hermite\)插值
  • yi=interp1(x , y , xi , 'pchip')
• \(cubic\)，三次多项式插值
  • yi=interp1(x , y , xi , 'cubic')
• \(v5cubic\)，matlab三次多项式函数插值
  • yi=interp1(x , y , xi , 'v5cubic')

插值方法	运算时间	内存占用	光滑程度
邻近点插值	快	少	差
线性插值	稍长	较多	稍好
三次样条插值	最长	较多	最好
三次\(Hermite\)插值	较长	少	较好

当\(x=0: 0.3 : 3\)时，对函数\(y=(x^{2}-4x+2) · sin(x)\)
求\(xi=0 : 0.01 : 3\)采用不同的方法进行插值

clear;
clc;
x = 0:0.3:3 % 0~3 间隔0.3
y = (x.^2-4*x+2).*sin(x);

xi = 0:0.01:3			% 0~3 间隔为0.1,插值的数据

yi_nearest = interp1(x,y,xi,'nearest');	%临近点插值
yi_linear = interp1(x,y,xi);	%默认为线性插值
yi_spine = interp1(x,y,xi,'spine');	%三次样条插值
yi_pchip = interp1(x,y,xi,'pchip');%分段三次Hermite插值
yi_v5cubic = interp1(x,y,xi,'v5cubic');%MATLAB5中三次多项式插值
figure;									
hold on;

subplot(2,3,1); %2行3列 从左到右，上到下第一个子图

plot(x,y,'ro');			%绘制数据点
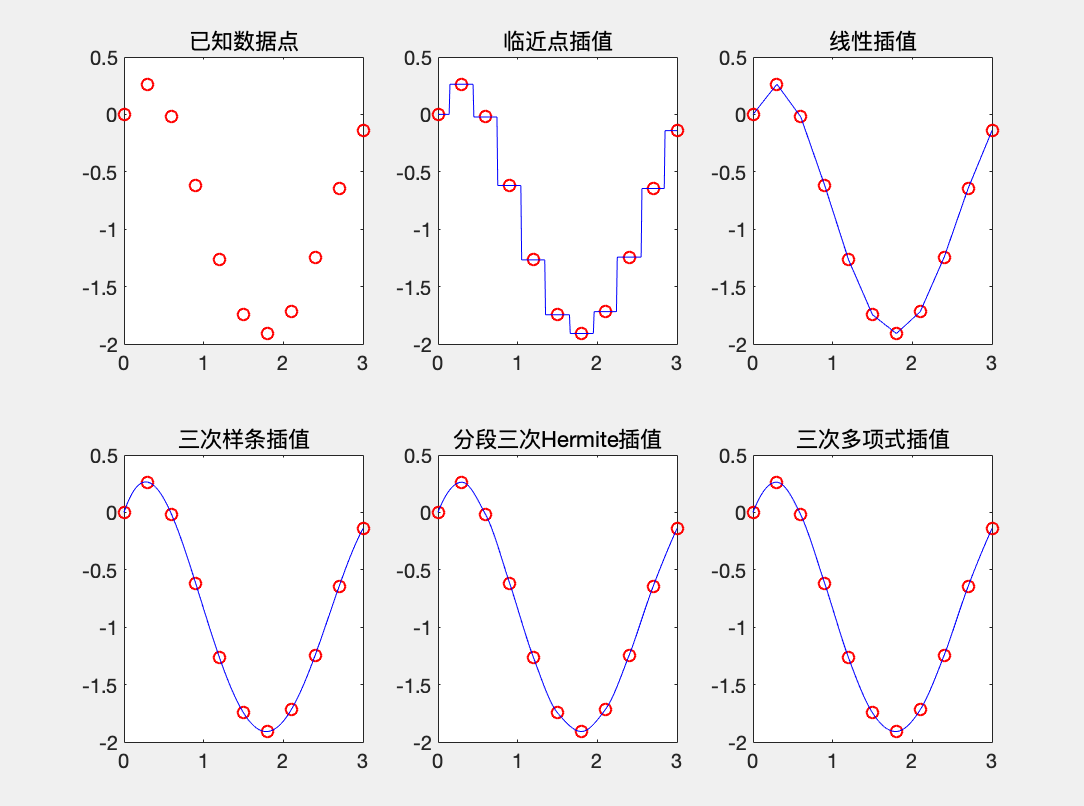
title('已知数据点');


subplot(2,3,2); % 同时画 多个图 
plot(x,y,'ro',xi,yi_nearest,'b-');	%绘制临近点插值的结果
title('临近点插值');

subplot(2,3,3);	
plot(x,y,'ro',xi,yi_linear,'b-');	%绘制线性插值的结果
title('线性插值');

subplot(2,3,4);
plot(x,y,'ro',xi,yi_spine,'b-');	%绘制三次样条插值的结果
title('三次样条插值');

subplot(2,3,5);
plot(x,y,'ro',xi,yi_pchip,'b-');	%绘制分段三次Hermite插值的结果
title('分段三次Hermite插值');

subplot(2,3,6);
plot(x,y,'ro',xi,yi_v5cubic,'b-');	%绘制三次多项式插值的结果
title('三次多项式插值');

2.3 二维插值

• 思想与一维插值基本一致，对函数\(z=f(x,y)\)进行插值
• 网格点
  • zi = interp2(x,y,z,xi,yi,'method'),要求(x,y)必须是严格单调的，如果数据是等间距的再method 前面+ * 提高速度
  • 要求x、y 要么全是矩阵要么x是行向量、y是列向量
• 散点
  • zi = griddata(x,y,z,xi,yi,'method')

clear;
clc;
[x,y] = meshgrid(-5:1:5)		%原始数据

z = peaks(x,y); %二元高斯概率密度分布函数

[xi,yi] = meshgrid(-5:0.01:5);						%插值数据

zi_nearest = interp2(x,y,z,xi,yi,'*nearest');		%临近点插值
zi_linear = interp2(x,y,z,xi,yi);					%默认线性插值
zi_spline = interp2(x,y,z,xi,yi,'*spline');		%三次样条插值
zi_cubic = interp2(x,y,z,xi,yi,'*cubic');			%三次多项式插值

figure;				%数据显示
hold on;
subplot(321);
meshc(x,y,z);			%绘制原始数据点
title('原始数据');

subplot(322);
meshc(xi,yi,zi_nearest);	%绘制临近点插值的结果
title('临近点插值');

subplot(323);
meshc(xi,yi,zi_linear);	%绘制线性插值的结果
title('线性插值');

subplot(324);
meshc(xi,yi,zi_spline);	%绘制三次样条插值的结果
title('三次样条插值');

subplot(325);
meshc(xi,yi,zi_cubic);	%绘制三次多项式插值的结果
title('三次多项式插值');